Вынужденные колебания систем с одной степенью свободы при действии вибрационной нагрузки

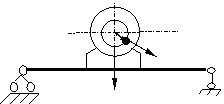
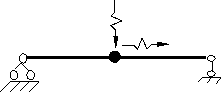
Вибрационную нагрузку создают машины с неуравновешенной вращающейся частью, масса которой имеет относительно оси вращения эксцентриситет r.

r

m₀

P

Psin Qt

Во время движения неуравновешенной массы возникает центробежная сила, определяемая по формуле

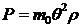(12)

где m₀ - масса неуравновешенной части, q = угловая скорость вращения массы m_0.

Если двигатель делает n оборотов в минуту, то угловая скорость будет определять и круговую частоту действующей нагрузки

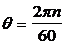(13)

где .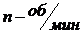

Если начало действия нагрузки считать от горизонтальной оси, то составляющие центробежной силы будут:

- вертикальная Р_у = Р sin q t

- горизонтальная P_x = P cos q t

PsinQt

PcosQt

m

Рассмотрим действие силы Р sin q t. Дифференциальное уравнение (6) в этом случае запишется:

,

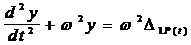где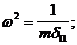

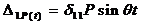
тогда:

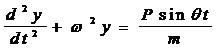(14)

где m - масса двигателя, включая и m₀.

Полное решение дифференциального уравнения (14):

y = A sin wt + B cos wt + Ф (15)

где

Ф = С + Д sin q t (16)

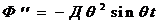
подставляя Ф и Ф’’ в уравнение (14) вместо у и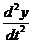

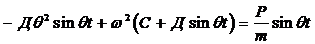(17)

при t = 0 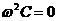т.к. 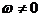то С = 0

Подставляя С = 0 и разделив уравнение (17) на sin qt, получим:

,

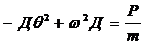или

.

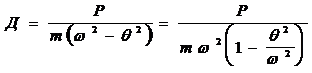из выражения:

,

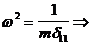
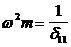или

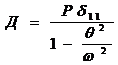
тогда:

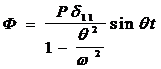(18)

Общее решение дифференциального уравнения (14) запишется:

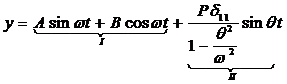(19)

Полное решение состоит из 2^х частей. I часть представляет собой решение однородного дифференциального уравнения и характеризует свободные колебания системы. При наличии самых незначительных сил сопротивления свободные колебания системы быстро затухают и остается II^я часть уравнения, которая представляет собой установившиеся вынужденные колебания при действии вибрационной нагрузки.

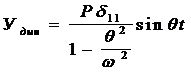(20)

Если обозначить У_ст(Р) = Рd₁₁ - прогиб от максимальной динамической нагрузки, при статическом ее действии, то

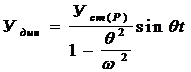21)

Максимальный динамический прогиб получим в том случае, если :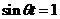

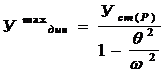
обозначим:

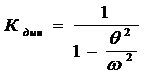(22)

где К_дин - динамический коэффициент при действии вибрационной нагрузки

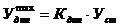
Зная К_дин мы можем рассчитывать систему на динамическую нагрузку как на статическую, если ее предварительно умножить на К_дин, т.е.

К_динP sin q t

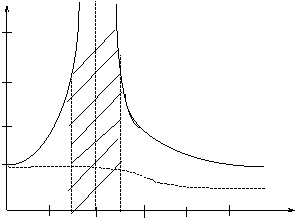
Построим график изменения динамического коэффициента (по абсолютной величине) в зависимости отношения 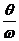, где w - частота собственных колебаний; q - вынужденные колебания.

[k_дин]

q=0; k_д=1

4 q®w;k_д ®¥

область резонанса

1

0.5 1 1.5 2 2.5 q/w

Рис. 1

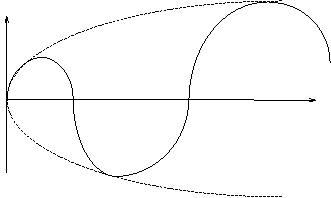y

t

Рис. 2. График нарастания колебаний при резонансе

Из рис.1 и рис.2 видно, что если частота вынуждающей силы приближается к частоте свободных колебаний, то наступает явление резонанса. Резонансной считается область .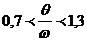

При резонансе колебания неограниченно возрастают, что на практике приводит к разрушению сооружения.

Учитывая сказанное, в динамических расчетах всегда необходимо определять частоту свободных колебаний w и сравнивать ее с частотой вынуждающей силы. Необходимо чтобы частота вынужденных колебаний q была меньше частоты свободных колебаний w, в противном случае при остановке и пуске двигателя возможно явление резонанса.

На практике требуется, чтобы .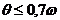

Для соблюдения этого условия обычно изменяют частоту свободных колебаний 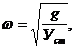т.к. частоту вынужденных колебаний q в большинстве случаев изменить нельзя.

Частота w увеличивается при увеличении жесткости сооружения, уменьшении длин пролетов и т.п.