Приближенное решение задачи коши методом эйлера
Лабораторная работа
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ МЕТОДОМ ЭЙЛЕРА
Теоретический минимум
Постановка задачи
Найти функцию у = у ( х ), удовлетворяющую дифференциальному уравнению
y¢ = f ( x, y ), x 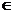 [ a, b ],
[ a, b ],
и принимающую в точке х = а заданное значение уа : у ( а ) = уа .
Задача нахождения такой функции называется задачей Коши. Если функция f ( x, y ) и ее частная производная f ¢y непрерывны при x 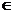 [ a, b ] и всех у, то решение задачи Коши существует и единственно.
[ a, b ] и всех у, то решение задачи Коши существует и единственно.
Как и в случае с интегрированием функции, не каждая задача Коши имеет решение, выражаемое через элементарные функции ( и даже через интегралы от элементарных функций ). И даже в случае, когда такое решение существует, часто поиск его из-за сложности функции f ( x, y ) вызывает определенные затруднения. Поэтому во многих практически важных случаях приходится находить приближенное решение задачи Коши. Методов приближенного решения задачи Коши, т.н. численных методов ее решения, достаточно много. В лабораторной работе рассматривается самый простой и наглядный из них – метод Эйлера.
Численный метод Эйлера
Пусть требуется найти приближенное решение дифференциального уравнения
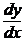 = f (x, y), (1)
= f (x, y), (1)
удовлетворяющее начальному условию
у(х0) = у0. (2)
Будем предполагать, что в некотором прямоугольнике
D = { | x – x0 | ≤ A, | y – y0 | ≤ B } функция f (x, y) непрерывна и имеет непрерывные частные производные достаточно высокого порядка по всем аргументам, так что решение задачи Коши (1) – (2) существует, единственно и является функцией, дифференцируемой достаточное число раз.
Численное решение задачи (1) – (2) состоит в построении таблицы приближенных значений y1, y2, …, yn решения задачи в точках х1, х2, …, хn. Чаще всего точки х1, х2, …, хn выбирают равноотстоящими: хk = х0 + k ∙ h ( k = 0, 1, 2, … , n ). Здесь х0 = а,
хn = b. Точки хk называют узлами сетки, величину h = 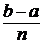 – шагом сетки.
– шагом сетки.
Так как, по определению, производная 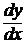 есть предел разностного отношения
есть предел разностного отношения 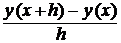 при h → 0, то, заменяя производную этим отношением, вместо дифференциального уравнения
при h → 0, то, заменяя производную этим отношением, вместо дифференциального уравнения
(1) получим разностное уравнение (разностную схему Эйлера)
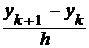 = f (xk, yk), k = 0, 1, 2, … , n ,
= f (xk, yk), k = 0, 1, 2, … , n ,
или
уk +1 = уk + h ∙ f (xk, yk), k = 0, 1, 2, … , n. (3)
Учитывая, что у0 = у(х0) – заданная величина, по рекуррентной формуле (3) последовательно находим значения уk = у(хk) во всех узлах сетки: по известным значениям х0 и у0 сначала вычисляется
у1 = у0 + h ∙ f (x0, y0).
Затем, зная х1 и у1, вычисляется
у2 = у1 + h ∙ f (x1, y1)
и т.д.
В результате вместо точного решения у = у(х) находится функция 








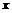
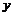
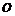
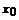
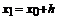
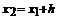
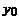
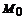
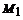
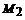

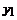

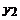
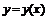
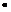 уk = у(хk) дискретного аргу-
уk = у(хk) дискретного аргу-
мента хk (сеточная функция), даю-
щая приближенное решение задачи
(1) – (2).
Геометрически искомая
интегральная кривая у = у(х), прохо-
дящая через точку М0(х0, у0), заменя-
ется т.н. ломаной Эйлера
М0 М1 М2 … Мn с вершинами в точ-
ках Мk (хk, уk) (рис. 1). При этом, на Рис.1.
каждом элементарном участке [хk, xk +1] угловой коэффициент отрезка Мk Мk +1 ломаной Эйлера равен f (xk, yk). Это значит, что данный отрезок представляет собой отрезок касательной, проведенной к интегральной кривой уравнения (1), проходящей через точку Мk (хk, уk).
Метод Эйлера относится к группе одношаговых методов, в которых для вычисления точки Мk +1 (хk +1, уk +1) требуется знание только предыдущей вычисленной точки Мk (хk, уk).
Для оценки погрешности метода на одном шаге сетки разложим точное решение у = у(х) в окрестности точки х = хk по формуле Тейлора
y(ормуле Тейлора
ки х = а одном шаге сетки разложим точное решение (хk +1) = y (ормуле Тейлора
ки х = а одном шаге сетки разложим точное решение (хk + h) = y(ормуле Тейлора
ки х = а одном шаге сетки разложим точное решение (хk) + y(ормуле Тейлора
ки х = а одном шаге сетки разложим точное решение (хk) ∙ h + O(h2) = y(ормуле Тейлора
ки х = а одном шаге сетки разложим точное решение (хk) + h ∙ f (xk, yk) + O(h2). (4)лько предыдущейтодов, в которых для
Сравнение формул (3) и (4) показывает, что они совпадают до членов первого порядка по h включительно, а погрешность формулы (4) равна O(h2). Поэтому говорят, что метод Эйлера имеет первый порядок точности.
Пример. Методом Эйлера для y¢= 2xy найти у(1), если у(0) = 1. Выбрать h = 0,1.
• Для расчетов составим таблицу
| k | xk | yk = yk –1+ Δ yk –1 | Δ yk = 2 xk yk ∙ h |
| 0,1 | 1 + 0 = 1 | 0,020 | |
| 0,2 | 1 + 0,02 = 1,02 | 0,041 | |
| 0,3 | 1,02 + 0,041 = 1,061 | 0,064 | |
| 0,4 | 1,061 + 0,064 = 1,125 | 0,090 | |
| 0,5 | 1,125 + 0,09 = 1,215 | 0,121 | |
| 0,6 | 1,215 + 0,121 = 1,336 | 0,160 | |
| 0,7 | 1,336 + 0,16 = 1,496 | 0,209 | |
| 0,8 | 1,496 + 0,209 = 1,705 | 0,273 | |
| 0,9 | 1,705 + 0,273 = 1,978 | 0,357 | |
| 1,978 + 0,357 = 2,335 |
В результате из последней строки таблицы получаем
у(1) ≈ 2,335.
Аналитическое решение:
y¢ = 2xy => 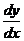 = 2xy =>
= 2xy => 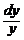 = 2x dx => ln y = x2 + ln C => y = C
= 2x dx => ln y = x2 + ln C => y = C 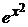 .
.
Из начальных условий имеем: y(0) = C 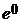 = С = 1.
= С = 1.
Таким образом, точное решение y = 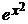 . Значение у(1) = е ≈ 2,718.
. Значение у(1) = е ≈ 2,718.
Уравнений 1-го порядка
Однородные уравнения
Дифференциальное уравнение 1-го порядка называется однородным,
если его можно привести к виду
y¢ = f 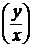 (5)
(5)
или к виду
M ( x, y ) dx + N ( x, y ) dy = 0, (6)
где M ( x, y ) и N ( x, y ) – однородные функции одного порядка, т.е. существует такое k 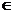 Z, что M ( t x, t y ) = t k M ( x, y ) и N ( t x, t y ) = t k N ( x, y ).
Z, что M ( t x, t y ) = t k M ( x, y ) и N ( t x, t y ) = t k N ( x, y ).
С помощью подстановки 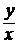 = u(x) (y = xu => y¢ = u + x u¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.
= u(x) (y = xu => y¢ = u + x u¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.
Пример 3.Решить уравнение y¢ = 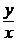 + cos
+ cos 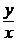 .
.
• Положим 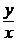 = u или y = xu. Тогда y¢ = u + x u¢, что после подстановки в исходное уравнение дает уравнение с разделяющимися переменными
= u или y = xu. Тогда y¢ = u + x u¢, что после подстановки в исходное уравнение дает уравнение с разделяющимися переменными
u + x u¢ = u + cos u или x 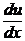 = cos u.
= cos u.
Разделяем переменные
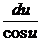 =
= 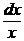
и интегрируем
tg 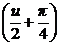 = Cx.
= Cx.
Получаем общее решение
u = 2 arctg Cx – 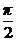 + 2πn, n
+ 2πn, n 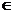 Z.
Z.
Возвращаясь к функции у, находим:
у = х 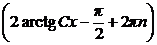 , n
, n 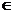 Z.
Z.
При делении на cos u были потеряны решения у = х 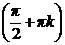 , k
, k 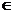 Z.
Z.
Добавляя их к полученному семейству решений, окончательно находим
у = х 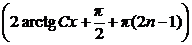 , n
, n 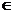 Z; у = х
Z; у = х 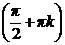 , k
, k 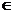 Z.
Z.
Линейные уравнения
Линейным дифференциальным уравнением 1-го порядка называется
уравнение вида
y¢ + p(x) y = q(x), (7)
где p(x) и q(x) – заданные и непрерывные на некотором промежутке функции.
Существует несколько методов интегрирования уравнения (7). Рассмотрим самый распространенный из них – метод Бернулли, называемый «методом u на v». Суть метода в том, что решение этого уравнения ищется в виде произведения
у = u v, (8)
где u = u(x), v = v (x) – неизвестные функции х, причем одна из этих функций произвольна (но не равна тождественно нулю).
Подставляя решение у = u v и его производную у¢ = u¢ v + u v¢ в уравнение (7), получим
u¢ v + u v¢ + p(x) u v = q(x) или u¢ v + u (v¢ + p(x) v) = q(x). (9)
Пользуясь произвольностью в выборе функции v (x), выберем ее так, чтобы выражение в скобках стало равным нулю
v¢ + p(x) v = 0. (10)
Это уравнение с разделяющимися переменными. Решив его и подставив выражение для v в (9), получим следующее уравнение относительно u
u¢ v = q(x). (11)
Решаем это уравнение, находим u = u(x,C). Таким образом, общее решение линейного уравнения (7) у = u(x,C) v.
Пример 4. Найти частное решение дифференциального
уравнения (решить задачу Коши) у¢ = 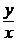 –
– 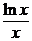 с начальными условиями у (1) = 1.
с начальными условиями у (1) = 1.
• Это линейное уравнение вида у¢ + p(x) y = q (x), в котором p(x) = – 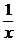 , q (x) = –
, q (x) = – 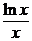 . Общее решение ищем в виде y = uv. Тогда y = u¢v + uv¢ . Имеем:
. Общее решение ищем в виде y = uv. Тогда y = u¢v + uv¢ . Имеем:
u¢v + uv¢ – 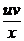 = –
= – 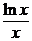 => u¢v + u
=> u¢v + u 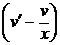 = –
= – 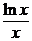 .
.
Подберем функцию v так, чтобы v¢ – 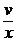 = 0; тогда u¢v = –
= 0; тогда u¢v = – 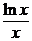 . Интегрируя первое из этих уравнений, получим:
. Интегрируя первое из этих уравнений, получим:
v¢ – 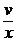 = 0 =>
= 0 => 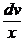 =
= 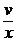 =>
=> 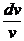 =
= 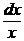 => ln | v | = ln | x | => v = х.
=> ln | v | = ln | x | => v = х.
Подставив полученное выражение для v во второе уравнение, получим:
u¢х = – 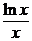 => du = –
=> du = – 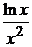 dx .
dx .
Интегрируем обе части данного уравнения: 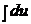 = –
= – 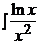 dx.
dx.
Второй интеграл берем по частям:
– 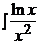 dx =
dx = 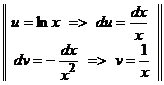 =
= 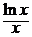 –
– 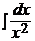 =
= 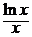 +
+ 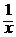 + C.
+ C.
Таким образом, u = 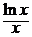 +
+ 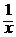 + C, а общее решение исходного уравнения
+ C, а общее решение исходного уравнения
y = uv = x 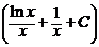 = ln x + 1 + Cx .
= ln x + 1 + Cx .
Подставим в это общее решение начальное условие:
1 = ln 1 + 1 + C ∙ 1 = 0 + 1 + C = 1 + C.
Отсюда получаем, что С = 0.
Таким образом, искомое частное решение имеет вид y = ln x + 1.
Уравнение Бернулли
Уравнением Бернулли называется дифференциальное уравнение 1-го порядка вида
y¢ + p(x) y = q(x) yn, (12)
где n ≠ 0, n ≠ 1 (при n = 0 уравнение (12) является линейным, а при n = 1 – уравнением с разделяющимися переменными). Проинтегрировать уравнение Бернулли можно так же, как и линейное уравнение с помощью подстановки у = u v.
Пример 5. Решить дифференциальное уравнение у¢ = 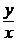 +
+ 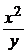 .
.
• Это уравнение Бернулли. Полагая у = u v, приведем исходное уравнение к виду u¢v + u 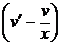 =
= 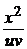 .
.
Решаем первое уравнение v¢ – 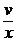 = 0:
= 0:
v¢ – 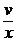 = 0 =>
= 0 => 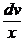 =
= 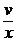 =>
=> 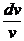 =
= 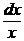 => ln | v | = ln | x | => v = х.
=> ln | v | = ln | x | => v = х.
Второе уравнение примет вид u¢х = 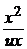 или u¢ =
или u¢ = 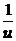 .
.
Решаем его: u¢ = 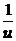 => u du = dx => u2 = 2x + C => u =
=> u du = dx => u2 = 2x + C => u = 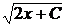 . Перемножая u и v, получим общее решение исходного уравнения
. Перемножая u и v, получим общее решение исходного уравнения
у = х 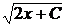 .
.
Программа на PASCALе
program ivanov_koshi_1; {y¢ = y/x – ln(x)/x, y(1)=1}
Var
x0,xn,y0,h,x,y,yt:real;
n,i:integer;
function prch(x,y:real):real; {правая часть}
Begin
prch:= y/x – ln(x)/x
end;
function anresh(x:real):real; {аналитическое решение}
Begin
anresh:= ln(x)+1
end;
Begin
writeln (‘введите начальные условия х0, xn, y0’);
read(x0,xn,y0); {ввод x0,xn,y0 }
writeln (‘введите число точек разбиения отрезка [х0, xn]’);
read(n); {ввод n }
h:=(xn–x0)/n;
writeln (‘ Р Е З У Л Ь Т А Т Ы’);{впереди 20 пробелов}
writeln;
writeln (‘ n = ’, n:0, ‘ h = ’, h:0:4);
writeln;
writeln (‘ x точн.реш. числ.реш. абс.ош. отн.ош’);{2,11,6,6,8 пробелов}
writeln;
x:=x0;
y:=y0;
yt:= anresh(x);
for i:=1 to n+1 do
Begin
writeln(x:7:3, yt:15:6, y:15:6, abs(yt–y):15:6, abs((yt–y)/yt):15:6);
y:=y+h*prch(x,y);
x:=x+h;
yt:= anresh(x);
end;
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
Р Е З У Л Ь Т А Т Ы
n = 5 h = 0.4000
1.00000 1.000000 1.000000 0.000000 1.000000
1.40000 1.336472 1.400000 0.063528 0.047534
1.80000 1.587787 1.703865 0.116078 0.073107
2.20000 1.788457 1.951882 0.163425 0.091378
2.60000 1.955511 2.163414 0.207903 0.106316
3.00000 2.098612 2.349246 0.250633 0.119428
Замечания.
1. Для получения «красивых» таблиц в PASCALе
а) в строковых константах (в кавычках) при наборе их латиницей количество символов должно быть таким же, как и в примере, где они набраны кириллицей;
б) количество пробелов в строковых константах также должно быть таким же, как и в примере. Для этого последовательность количества пределов в строковой константе представлена в комментарии.
2. Так как возможности по объему «черного экрана» в Паскале
ограничены, желательно в программе задавать размер «сетки» с n ≤ 10.
3. Следует обратить внимание на запись операции деления.
Например, правильная запись дроби 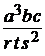 может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.
может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.
4. Другая особенность данного этапа состоит в ограниченности
библиотеки встроенных функций PASCALя. Для записи встречающихся в заданиях функций используются функции
sin(x), cos(x), sqrt(x) ( 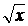 ), sqr(x) (x2), arctan(x) (arctg x), ln(x), abs(x) (|x|), а также постоянная pi (π).
), sqr(x) (x2), arctan(x) (arctg x), ln(x), abs(x) (|x|), а также постоянная pi (π).
Для записи других функций следует пользоваться тождественными формулами :
tg x = 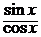 , arcsin x = arctg
, arcsin x = arctg 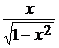 , xa = ealnx,
, xa = ealnx,
arcctg x = 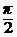 – arctg x, arccos x = arcctg
– arctg x, arccos x = arcctg 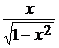 .
.
Еще два замечания:
1) Так как встроенная функция sqr(x) выполняется значительно дольше, чем операция * (умножение), то при возведении в целую степень при небольших значениях показателя степени желательно использовать операцию умножения.
2) Если в выражении функции некоторая степень встречается несколько раз, ее желательно вычислить один раз и в дальнейшем использовать вычисленное значение. Например, функцию
y = x5 + sin(x5 + x4 – x3) можно описать так:
function primer (x:real):real;
y:real;
Begin
y:= x*x*x*x*x;
primer:= y+sin(y+y/x–y/x/x)
end;
Рабочая область Mathcad’а нахождения частного решения дифференциального уравнения y´ = 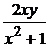 + 1 + x2 с начальными условиями у(1) = 1 представлена ниже. Однако, вначале найдем
+ 1 + x2 с начальными условиями у(1) = 1 представлена ниже. Однако, вначале найдем
аналитическое решение данной задачи Коши.
• Это линейное уравнение вида у¢ + p(x) y = q (x), в котором
p(x) = – 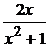 , q (x) = 1 + x2. Общее решение ищем в виде y = uv . Тогда y = u¢v + uv¢ . Имеем:
, q (x) = 1 + x2. Общее решение ищем в виде y = uv . Тогда y = u¢v + uv¢ . Имеем:
u¢v + uv¢ – 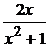 uv = 1 + x2 => u¢v + u
uv = 1 + x2 => u¢v + u 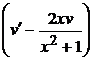 = 1 + x2.
= 1 + x2.
Подберем функцию v так, чтобы v¢ – 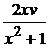 = 0; тогда u¢v = 1 + x2. Интегрируя первое из этих уравнений, получим: v¢ –
= 0; тогда u¢v = 1 + x2. Интегрируя первое из этих уравнений, получим: v¢ – 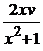 = 0 => =>
= 0 => => 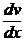 =
= 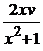 =>
=> 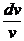 =
= 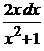 => ln |v| = ln |1 + x2| => v = 1 + x2.
=> ln |v| = ln |1 + x2| => v = 1 + x2.
Подставив полученное выражение для v во второе уравнение, получим:
u¢(1 + x2) = 1 + x2 или 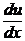 = 1 .
= 1 .
Таким образом, u = х + C, а общее решение исходного уравнения
y = uv = (х + C) (1 + x2) = x3 + C x2 + х + С .
Подставим в это общее решение начальное условие и получим:
1 = 1 + С + 1 + С => C = – 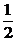 .
.
Искомое частное решение имеет вид y = x3 – 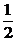 x2 + х –
x2 + х – 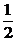 .
.
ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
Методом Эйлера найти численное решение следующих задач Коши (по выбору преподавателя из каждого варианта выбираются две задачи: одна для составления программы, другая – для ручного расчета):
1. a) y′ – 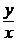 = x2, y(1) = 0; (y = 0,5 x (x2 - 1))
= x2, y(1) = 0; (y = 0,5 x (x2 - 1))
b) y′ + xy = (1 + x) e–x y2, y(0) = 1; (y = ex)
c) Скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды (закон Ньютона). Найти зависимость температуры T от времени t, если тело, нагретое до
T0 = 100о С градусов, внесено в помещение, температура которого постоянна и равна a = 20оС. Через какое время температура тела опустится до 60 оС (принять k = 2 )? (T = a + (T0 – a) e –k t, t = ln 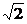 )
)
2. a) y′ = 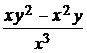 , y(–1) = 1; ( y =
, y(–1) = 1; ( y = 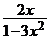 )
)
b) xy′ + y = 2y2 ln x, y(1) = 0,5; ( y = 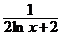 )
)
c) Через сколько времени температура тела, нагретого до 100оС, понизится до 25оС, если температура помещения равна 20оС и за первые 10 мин тело охладилось до 60оС? (Через 40 мин)
3. a) (y2 + xy) d x – x2 dy = 0, y(1) = 1; ( y = 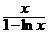 )
)
b) 2(xy′ + y) = xy2, y(1) = 2; ( y = 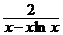 )
)
c) Ж/д состав движется со скоростью 20 км/час. Через одну минуту после выключения двигателя его скорость уменьшилась до 2 км/час. Определить скорость состава через две минуты после остановки двигателя, считая сопротивление движению пропорциональным скорости. (0,2 км/час)
4. a) xy′ – y + x 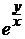 = 0, y(e) = 0; (y = -x lnlnx)
= 0, y(e) = 0; (y = -x lnlnx)
b) y′ + 4 x3 y = 4(x3 + 1) e–4x y2, y(0) = 1; (y = x4)
c) Тело движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент тело имело скорость v0 = 15 м/с и находилось на расстоянии 4 м от начала отсчета пути. Определить скорость тела через 8 с после начала движения. ( 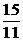 м/с)
м/с)
5. a) y′ – 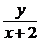 = x2 + 2х, y(–1) =
= x2 + 2х, y(–1) = 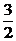 ; ( y = (x + 2) (1 + 0,5x2))
; ( y = (x + 2) (1 + 0,5x2))
b) xy′ = y + x sin 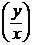 , y(1) =
, y(1) = 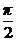 ; ( y = 2x tg(1/x))
; ( y = 2x tg(1/x))
c) Составить дифференциальное уравнение изменения скорости ж/д состава массы m = 10 000 тонн, движущегося со скоростью v0 = 10 м/с, при замедленном прямолинейном движении под действием силы сопротивления, пропорциональной квадрату скорости и равной 20000 Н при скорости 1 м/с. Определить какое расстояние пройдет состав после выключения двигателя, прежде чем его скорость уменьшится до 2 м/с .
(v´= – 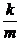 v2; 200 )
v2; 200 )
6. a) y′ – 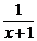 y = ex (x + 1), y(0) = 1; ( y = ex (x + 1))
y = ex (x + 1), y(0) = 1; ( y = ex (x + 1))
b) xy′ = y + 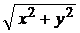 , y(0) = –1; ( y = 0,25 (x2 - 4))
, y(0) = –1; ( y = 0,25 (x2 - 4))
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен –1% .
( 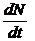 = kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
= kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
7. a) y′ – 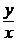 = x sinx, y(π/2) = 1; ( y = 2x/π - xcosx)
= x sinx, y(π/2) = 1; ( y = 2x/π - xcosx)
b) xy′ – y (lny – lnx) = 0, y(–1) = –1; ( y = x ex+1)
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен 2% .
( 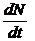 = kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
= kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
8. a) y′ + 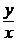 = sinx, y(π) =
= sinx, y(π) = 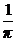 ; ( y = sinx/x – 1/2x – cosx)
; ( y = sinx/x – 1/2x – cosx)
b) y′ = 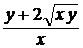 , y(1) = 1; ( y =
, y(1) = 1; ( y = 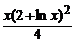 )
)
c) В благоприятных для размножения условиях находится некоторое количество N0 бактерий. Найти зависимость увеличения числа бактерий от времени, если скорость размножения бактерий пропорциональна их количеству. Через сколько времени количество бактерий увеличится втрое? (N = N0 ek t ; t = 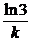 )
)
9. a) y′ + 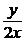 = x2, y(1) = 1; ( y = 5/(7
= x2, y(1) = 1; ( y = 5/(7 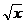 ) + 2x3/7)
) + 2x3/7)
b) 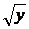 (2
(2 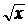 –
– 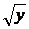 ) dx + x dy = 0, y(1) = 0; ( y = x ln2x)
) dx + x dy = 0, y(1) = 0; ( y = x ln2x)
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить через сколько времени после начала процесса останется лишь 1% первоначальной массы исходного вещества. (7,84 ч)
10. a) 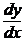 –
– 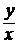 (1 + ln y – ln x) =0, y(1) = e; ( y = x ex)
(1 + ln y – ln x) =0, y(1) = e; ( y = x ex)
b) 3y′ + 2 xy = 2x y –2 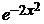 , y(0) = –1; ( y =
, y(0) = –1; ( y = 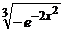 )
)
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить массу вещества в начале процесса.
(56,5 г)
11. a) y′ – 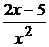 y = 5, y(2) =4; ( y = x2)
y = 5, y(2) =4; ( y = x2)
b) x dy = (x + y) dx, y(1) = 0; ( y = x lnx)
c) В баке находится 100 л раствора, содержащего 10 кг соли. В бак вливается вода со скоростью 5 л/мин, и смесь вытекает из него с той же скоростью. Однородность раствора достигается путем перемешивания. Сколько соли останется в баке через час? (0,5 кг)
12. a) (x2 – 3y2) dx + 2x y dy = 0, y(2) = 1; ( y = ± x 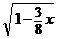 )
)
b) 3xy′ + 5y = (4x – 5) y4, y(1) = 1; ( y = 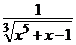 )
)
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Какой путь пройдет состав до остановки? (≈ 15 м)
13. a) y′ – 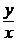 = –2
= –2 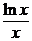 , y(1) = 1; ( y = 2lnx – x +2)
, y(1) = 1; ( y = 2lnx – x +2)
b) (x2 + y2 + xy) dx – x2 dy = 0, y(1) = 0; ( y = x tg lnx)
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Когда скорость уменьшится до 1 см/с? (≈ 50 с)
14. a) x2y′ + xy – x2 – y2 = 0, y(1) = 0; ( y = 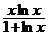 )
)
c) 3(xy′ + y) = x y2, y(1) = 3; ( y = 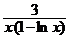 )
)
d) Скорость распада радия пропорциональна наличному его количеству. В течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия? (Через 1575 лет)
15. a) x2 – 3y2 + 2 x y y′ =0, y(–2) = 2; ( y = –x)
b) y′ – y = 2x y 2, y(0) = 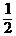 ; ( y =
; ( y = 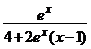 )
)
c) Скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды (закон Ньютона). Найти зависимость температуры T от времени t, если тело, нагретое до
T0 = 100о С градусов, внесено в помещение, температура которого постоянна и равна a = 20оС. Через какое время температура тела опустится до 60 оС (принять k = 2 )? (T = a + (T0 – a) e –k t, t = ln 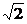 )
)
16. a) y′ = 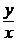 ln
ln 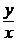 , y(1) = e; ( y = ex)
, y(1) = e; ( y = ex)
b) 2x y′ – 3y = –(20x 2 + 12) y3 , y(1) = 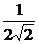 ; ( y =
; ( y = 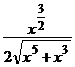 )
)
c) Через сколько времени температура тела, нагретого до 100оС, понизится до 25оС, если температура помещения равна 20оС и за первые 10 мин тело охладилось до 60оС? (Через 40 мин)
17. a) y′ – 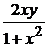 = 1 + x2, y(1) = 3; ( y =
= 1 + x2, y(1) = 3; ( y = 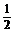 (x2+1) + x3+ x)
(x2+1) + x3+ x)
b) (2x – y) dx – x dy = 0, y(1) =1; ( y = x )
c) Ж/д состав движется со скоростью 20 км/час. Через одну минуту после выключения двигателя его скорость уменьшилась до 2 км/час. Определить скорость состава через две минуты после остановки двигателя, считая сопротивление движению пропорциональным скорости. (0,2 км/час)
18. a) y′ + 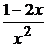 y = 1, y(1) = 1; ( y = x2)
y = 1, y(1) = 1; ( y = x2)
b) xy′ + y = y2ln x, y(1) =1; ( y = 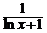 )
)
c) Тело движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент тело имело скорость v0 = 15 м/с и находилось на расстоянии 4 м от начала отсчета пути. Определить скорость тела через 8 с после начала движения. ( 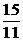 м/с)
м/с)
19. a) y′ + 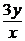 =
= 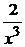 , y(1) = 1; ( y =
, y(1) = 1; ( y = 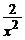 –
– 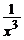 )
)
b) 2 y′ + 3y cos x = (8 + 12 cos x) e2x y –1 , y(0) = 2; ( y = 2ex )
c) Составить дифференциальное уравнение изменения скорости ж/д состава массы m = 10 000 тонн, движущегося со скоростью v0 = 10 м/с, при замедленном прямолинейном движении под действием силы сопротивления, пропорциональной квадрату скорости и равной 20000 Н при скорости 1 м/с. Определить какое расстояние пройдет состав после выключения двигателя, прежде чем его скорость уменьшится до 2 м/с .
(v´= – 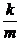 v2; 200 )
v2; 200 )
20. a) y′ +2xy =–2 x3, y(1) = e –1 ; ( y = 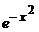 – x2 + 1 )
– x2 + 1 )
b) 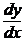 –
– 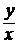 (1 + ln y – ln x) =0, y(1) = e; ( y = xex )
(1 + ln y – ln x) =0, y(1) = e; ( y = xex )
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен –1% .
( 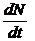 = kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
= kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
21. a) 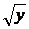 (2
(2 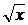 –
– 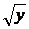 ) dx + x dy = 0, y(1) = 0; ( y = x ln2x )
) dx + x dy = 0, y(1) = 0; ( y = x ln2x )
b) 8xy′ – 12 y = –(5
