Перевод чисел из одной системы счисления в другую.

Лабораторная работа №1. «Математические основы работы ЭВМ. Системы счисления. Перевод чисел из одной системы счисления в другую. Математические основы работы ЭВМ. Алгебраическое представление двоичных чисел. Правила недесятичной арифметики».

1. Цель работы:

1.1. Изучить используемые в ЭВМ системы счисления.

1.2. Изучить способы представления цифр в различных системах счисления.

1.3. Научиться переводить числа из одной системы счисления в другую.

1.4. Изучить коды, используемые в ЭВМ для алгебраического представления чисел.

1.5. Изучить правила выполнения арифметических операций над числами в недесятичных системах счисления.

2. Общие сведения.

Современное написание цифр привычной для нас десятичной системы счисления пришло к нам из Индии через арабские страны. Само слово «цифра» происходит от арабского «сифр». Поэтому мы и называем используемые нами цифры «арабскими». В XIII в. этими цифрами стали пользоваться жители средневековой Италии, которые позаимствовали их у флорентийских купцов, торговавших с арабами. А уже к XV в. использование так называемых арабских цифр стало повсеместным.

Счислениемназывается совокупность приемов наименования и обозначения чисел.

Сегодня человек использует различные системы счисления. Как правило, эти системы различаются между собой количеством используемых для обозначения различных чисел цифр. В зависимости от способа изображения чисел, системы счисления делятся на:

- позиционные;

- непозиционные.

В позиционнойсистеме счисления цифры изменяют своё количественное значение в зависимости от их расположения в числе. Например, в числе 1841,21 имеются три цифры «1». Все они имеют разные значения. Первая обозначает тысячи, вторая единицы, а третья сотые доли соответственно. Указанное число является сокращенной записью следующей суммы:

1841,21₁₀ = 1۰10³ + 8۰10² + 4۰10 + 1 + 2۰10^-1 + 1۰10^-2

Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в диапазоне от 0 до Р-1. Для предотвращения разночтений основание системы счисления будем записывать в виде нижнего индекса справа от числа.

В общем случае запись любого смешанного числа в системе счисления с основание Р будет представлять собой сумму вида:

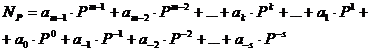(1)

Нижние индексы определяют местоположение цифры в числе (разряд):

- положительные значения индексов – для целой части числа (m разрядов);

- отрицательные значения индексов – для дробной части числа (s разрядов).

Максимальное целое число, которое может быть представлено в m разрядах:

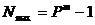(2)

Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части:

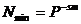(3)

Имея в целой части числа m, а в дробной – s разрядов, можно записать всего 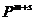разных чисел.

В двоичной системе счисления, основание которой Р=2 используется только две цифры 0 и 1. При этом единица каждого разряда равна двум единицам предыдущего разряда. Слева от разряда единиц расположены разряды двоек, затем четверок, восьмерок и. т. д. Чтобы записать число в двоичной системе счисления, нужно представить его в виде суммы последовательных степеней числа 2, умноженных на 0 или 1:

1841,25 = 1۰2¹⁰ + 1۰2⁹ + 1۰2⁸ + 0۰2⁷ + 0۰2⁶ + 1۰2⁵ +

+1۰2⁴ + 0۰2³ + 0۰2² + 0۰2¹ + 1۰2⁰ + 0۰2^-1 +1۰2^-2

Таким образом (1841,25)₁₀ = (11100110001,01)₂.

При представлении чисел в двоичной системе счисления приходится оперировать огромным количеством нулей и единиц, что не всегда удобно при ручном счете или при вводе в ЭВМ, поэтому в вычислительной технике довольно широко применяются также и другие системы счисления, прежде всего восьмеричная и шестнадцатеричная.

В восьмеричнойсистеме счисления, основание которой Р=8 используется восемь цифр 0, 1, 2, 3, 4, 5, 6, 7. При этом единица каждого разряда равна восьми единицам предыдущего разряда. Чтобы записать число в восьмеричной системе счисления, нужно представить его в виде суммы последовательных степеней числа 8, умноженных на цифры от 0 до 7:

3468₈ = 3۰8³ + 4۰8² + 6۰8¹ + 1۰8⁰ = 1841₁₀

Таким образом (1841)₁₀ = (3468)₈.

В шестнадцатеричнойсистеме счисления, основание которой Р=16 используется шестнадцать знаков – цифры от 0до 9, а также буквы A, B, C, D, E, F. При этом единица каждого разряда равна шестнадцати единицам предыдущего разряда. Чтобы записать число в шестнадцатеричной системе счисления, нужно представить его в виде суммы последовательных степеней числа 16, умноженных на цифры от 0 до 9 и буквы от A до F:

(262F)₁₆ = 2۰16³ + 6۰16² + 2۰16¹ + F۰16⁰ = 9775₁₀

Таким образом (9775)₁₀ = (262F)₁₆.

Представление чисел в шестнадцатеричной системе счисления оказывается гораздо компактнее, поскольку каждая группа из четырех двоичных цифр заменяется одним символом.

Титульный лист.

Ход выполнения работы.

В лабораторных работах №1 - 4 в отчет необходимо поместить не только собранные схемы, но и полученные для них графики зависимостей на логическом анализаторе.

В лабораторных работах №5 - 11 в отчет необходимо поместить не только собранные схемы, но и рисунки (скриншоты), иллюстрирующие правильное функционирование собранных в соответствии с заданием схем.

Лабораторная работа №1. «Математические основы работы ЭВМ. Системы счисления. Перевод чисел из одной системы счисления в другую. Математические основы работы ЭВМ. Алгебраическое представление двоичных чисел. Правила недесятичной арифметики».

1. Цель работы:

1.1. Изучить используемые в ЭВМ системы счисления.

1.2. Изучить способы представления цифр в различных системах счисления.

1.3. Научиться переводить числа из одной системы счисления в другую.

1.4. Изучить коды, используемые в ЭВМ для алгебраического представления чисел.

1.5. Изучить правила выполнения арифметических операций над числами в недесятичных системах счисления.

2. Общие сведения.

Современное написание цифр привычной для нас десятичной системы счисления пришло к нам из Индии через арабские страны. Само слово «цифра» происходит от арабского «сифр». Поэтому мы и называем используемые нами цифры «арабскими». В XIII в. этими цифрами стали пользоваться жители средневековой Италии, которые позаимствовали их у флорентийских купцов, торговавших с арабами. А уже к XV в. использование так называемых арабских цифр стало повсеместным.

Счислениемназывается совокупность приемов наименования и обозначения чисел.

Сегодня человек использует различные системы счисления. Как правило, эти системы различаются между собой количеством используемых для обозначения различных чисел цифр. В зависимости от способа изображения чисел, системы счисления делятся на:

- позиционные;

- непозиционные.

В позиционнойсистеме счисления цифры изменяют своё количественное значение в зависимости от их расположения в числе. Например, в числе 1841,21 имеются три цифры «1». Все они имеют разные значения. Первая обозначает тысячи, вторая единицы, а третья сотые доли соответственно. Указанное число является сокращенной записью следующей суммы:

1841,21₁₀ = 1۰10³ + 8۰10² + 4۰10 + 1 + 2۰10^-1 + 1۰10^-2

Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в диапазоне от 0 до Р-1. Для предотвращения разночтений основание системы счисления будем записывать в виде нижнего индекса справа от числа.

В общем случае запись любого смешанного числа в системе счисления с основание Р будет представлять собой сумму вида:

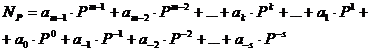(1)

Нижние индексы определяют местоположение цифры в числе (разряд):

- положительные значения индексов – для целой части числа (m разрядов);

- отрицательные значения индексов – для дробной части числа (s разрядов).

Максимальное целое число, которое может быть представлено в m разрядах:

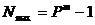(2)

Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части:

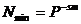(3)

Имея в целой части числа m, а в дробной – s разрядов, можно записать всего 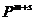разных чисел.

В двоичной системе счисления, основание которой Р=2 используется только две цифры 0 и 1. При этом единица каждого разряда равна двум единицам предыдущего разряда. Слева от разряда единиц расположены разряды двоек, затем четверок, восьмерок и. т. д. Чтобы записать число в двоичной системе счисления, нужно представить его в виде суммы последовательных степеней числа 2, умноженных на 0 или 1:

1841,25 = 1۰2¹⁰ + 1۰2⁹ + 1۰2⁸ + 0۰2⁷ + 0۰2⁶ + 1۰2⁵ +

+1۰2⁴ + 0۰2³ + 0۰2² + 0۰2¹ + 1۰2⁰ + 0۰2^-1 +1۰2^-2

Таким образом (1841,25)₁₀ = (11100110001,01)₂.

При представлении чисел в двоичной системе счисления приходится оперировать огромным количеством нулей и единиц, что не всегда удобно при ручном счете или при вводе в ЭВМ, поэтому в вычислительной технике довольно широко применяются также и другие системы счисления, прежде всего восьмеричная и шестнадцатеричная.

В восьмеричнойсистеме счисления, основание которой Р=8 используется восемь цифр 0, 1, 2, 3, 4, 5, 6, 7. При этом единица каждого разряда равна восьми единицам предыдущего разряда. Чтобы записать число в восьмеричной системе счисления, нужно представить его в виде суммы последовательных степеней числа 8, умноженных на цифры от 0 до 7:

3468₈ = 3۰8³ + 4۰8² + 6۰8¹ + 1۰8⁰ = 1841₁₀

Таким образом (1841)₁₀ = (3468)₈.

В шестнадцатеричнойсистеме счисления, основание которой Р=16 используется шестнадцать знаков – цифры от 0до 9, а также буквы A, B, C, D, E, F. При этом единица каждого разряда равна шестнадцати единицам предыдущего разряда. Чтобы записать число в шестнадцатеричной системе счисления, нужно представить его в виде суммы последовательных степеней числа 16, умноженных на цифры от 0 до 9 и буквы от A до F:

(262F)₁₆ = 2۰16³ + 6۰16² + 2۰16¹ + F۰16⁰ = 9775₁₀

Таким образом (9775)₁₀ = (262F)₁₆.

Представление чисел в шестнадцатеричной системе счисления оказывается гораздо компактнее, поскольку каждая группа из четырех двоичных цифр заменяется одним символом.

Перевод чисел из одной системы счисления в другую.

Перевод целых чисел из десятичной системы в двоичную можно осуществить при помощи многократного деления на 2.

Рассмотрим следующий пример. Для записи числа (95)₁₀ в двоичной системе необходимо найти такие цифры 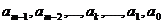(см. выражение (1)), равные 0 или 1, чтобы

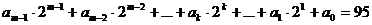(4)

Разделим правую и левую части равенства на 2. При этом в частном от деления левой части на 2 получим 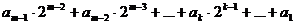а в остатке число 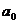. Получившееся частное и остаток равняются частному и остатку от деления правой части равенства (4) на 2, поэтому

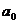=1

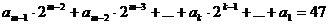
Разделим теперь опять обе части на 2, в результате будем иметь:

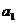=1

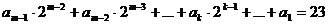
Аналогичным образом найдем значения остальных цифр .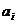

Таким образом, в результате получим: .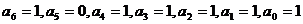

Следовательно:

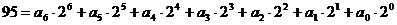т.е. (95)₁₀ = (1011111)₂.

Таким образом, нахождение двоичных цифр числа сводится к последовательному делению соответствующих частных на 2 и нахождению остатков от деления. Чтобы не выписывать каждый раз новые равенства, удобно пользоваться такой записью:

95 2

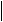
94 47 2

146 23 2

122 11 2

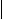
1 10 5 2

1 4 2 2

1 2 1 2

0

Выделенные полужирным шрифтом цифры есть остатки, которые и являются цифрами при записи числа 95 в двоичной системе счисления. Сначала получается цифра разряда единиц, потом цифра разряда двоек и так далее, т.е. цифры остатков выписываются в обратном порядке.

Можно пользоваться более простой формой записи:

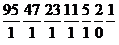
Над чертой записывают заданное число и получающиеся частные, под чертой – остатки от деления соответствующих частных на 2.

В двоичной системе счисления могут быть представлены не только целые, но и дробные числа. Для перевода дробного числа из десятичной системы счисления в двоичную нужно отдельно перевести целую (как показано выше) и дробную части числа. Дробная часть десятичного числа в двоичной системе представляется как сумма отрицательных степеней числа 2, умноженных на 1 или 0.

Рассмотрим, как осуществляется перевод дробной части в двоичную систему счисления. Пусть, например, в двоичной системе счисления требуется записать число (0,6875)₁₀. Для этого нужно найти такие цифры 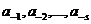равные 0 или 1, чтобы

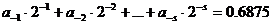
Умножим обе части этого выражения на 2:

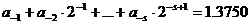
В левой части этого равенства цифра 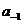есть целая часть числа в правой части (т.е. 1), а сумма остальных слагаемых составляют дробную часть, поэтому 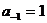, тогда

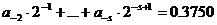
Опять умножим обе части на 2:

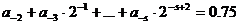
Отсюда 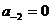, а остальные слагаемые равны 0,75.

Снова повторим операцию умножения:

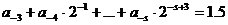
Следовательно 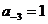, а сумма остальных слагаемых 0,5.

Т.е. 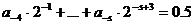, после умножения этого равенства на 2 получим 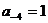. Поскольку дробная часть равна 0 (результат умножения 0,5 на 2 можно записать как 1,000…000), то и все остальные цифры 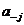равны 0.

Таким образом, (0,6875)₁₀ = (0,1011)₂. Приведенные вычисления удобнее записать в следующем виде:

0,6875

х 2

1,375

0,375

х 2

0,750

х 2

1,50

0,50

х 2

1,0

Цифры, выделены полужирным шрифтом, и являются искомыми двоичными цифрами, при этом в отличие от записи целой части, первой получается цифра, стоящая сразу после запятой.

Следует заметить, что не всегда дробное число, представленное конечным числом разрядов дробной части в одной системе счисления, можно записать конечным числом разрядов дробной части в другой системе счисления. Этим объясняется наличие погрешности при обработке информации с помощью вычислительных устройств, основанных на двоичной системе счисления.

Рассмотренные выше способы перевода из десятичной системы счисления в двоичную применимы, в общем случае, для перевода чисел из десятичной системы счисления в систему счисления с произвольным основанием P. Для этого деление и умножение целой и дробной частей исходного числа производят на основание P. Остатки от деления и последнее частное, которые при этом получаются, и являются искомыми цифрами числа в системе счисления с основанием P.

Очень простые правила действуют для перевода чисел из системы счисления P₁ в систему счисления P₂, где P₁ и P₂ являются степенями числа 2.

Рассмотрим для примера перевод числа из восьмеричной системы счисления в двоичную и наоборот. Для этого следует каждую восьмеричную цифру заменить тройкой двоичных цифр, в соответствие с таблицей 1.1

При переводе из двоичной системы счисления в восьмеричную разбивают двоичное число справа налево на группы из трех двоичных цифр, называемые триадами. Сначала выделяют крайнюю правую триаду (последние три цифры двоичной записи перед запятой), затем следующую (три цифры слева от крайней триады) и т.д. Если в последней триаде остается менее трех цифр, то вместо недостающих цифр слева записываются нули. Заменив каждую триаду соответствующей восьмеричной цифрой, получают число, записанное в восьмеричной системе счисления.

Таблица 1.1. Перевод чисел 8-2.

№ п/п	Число в восьмеричной системе	Число в двоичной системе (триада)

Например, двоичное число 11 001 101 разбивается на следующие триады: 011; 001; 101. Поскольку (011)₂ = (3)₈, (001)₂ = (1)₈, (101)₂ = (5)₈, то в восьмеричной системе счисления это будет число 315.

Таким образом (11001101)₂ = (315)₈.

При переводе дробной части числа разбиение на триады ведется слева направо, начиная с первого разряда после запятой. Если в последней справа триаде остаётся менее трёх цифр, то вместо недостающих цифр справа записываются нули.

Например: 0,101 001 100 = (0,514)₈

Аналогичные правила действуют и при переводе из десятичной системы счисления в шестнадцатеричную. При этом двоичное число разбивают на тетрады из четырех цифр каждая. Разбиение ведётся справа налево от запятой для целой части числа и слева направо от запятой для дробной части числа. Заменив каждую тетраду соответствующей шестнадцатеричной цифрой, получают число, записанное в шестнадцатеричной системе счисления. Соответствие двоичных тетрад и шестнадцатеричных цифр приведены в таблице 1.2.

Таблица 1.2. Перевод чисел.

№ п/п	Число в шестнадцатеричной системе	Число в двоичной системе (тетрада)
	A
	B
	C
	D
	E
	F

Например, двоичное число 1011001101 разбивается на следующие тетрады: 0010; 1100; 1101. Поскольку (0010)₂ = (2)₁₆, (1100)₂ = (C)₁₆, (1101)₂ = (D)₁₆, то в шестнадцатеричной системе счисления это будет число 2СD, т.е. (1011001101)₂ = (2CD)₁₆.

Алгебраическое представление двоичных чисел, то есть представления чисел с учетом их знака включает в себя арифметическое представление числа и знаковый разряд. При этом код «0» означает знак «+» (плюс), код «1» – знак «–« (минус). Для алгебраического представления чисел в вычислительных машинах используют специальные коды:

- прямой код числа;

- обратный код числа;

- дополнительный код числа.

Два последних кода позволяют заменить неудобную для ЭВМ операцию вычитания на операцию сложения с соответствующим отрицательным числом.

Дополнительный код обеспечивает более быстрое выполнение операций, поэтому чаще всего в ЭВМ применяется именно он.

Прямой код числа N – [N]_пр. Пусть N = a₁ a₂ a₃ … a_m. Тогда:

- если N>0, то [N]_пр = 0, a₁ a₂ a₃ … a_m;

- если N<0, то [N]_пр = 1, a₁ a₂ a₃ … a_m;

- если N=0, то имеет место неоднозначность: [0]_пр = 0,0… или 1,0…;

В общем виде:

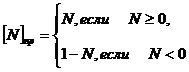
Обратный код числа N – [N]_обр.

Обозначение 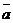означает величину, обратную 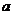(инверсию 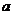), то есть если 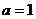, то 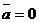, и наоборот.

- если N>0, то [N]_обр = [N]_пр = 0, a₁ a₂ a₃ … a_m;

- если N<0, то [N]_обр = ;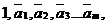

- если N=0, то имеет место неоднозначность: [0]_обр = 0, 0… или 1,11…1.

Обратный код положительного числа совпадает с прямым кодом. Для того чтобы получить обратный код отрицательного числа, необходимо цифры этого числа инвертировать, то есть во всех значащих разрядах нули заменить единицами, а единицы нулями, в знаковом разряде поставить 1.

Например, число N = 0,1011, [N]_обр = 0,1011.

Число N = - 0,1011, [N]_обр = 1,0100. В случае, когда N<0, [N]_обр = 10-1 10^-n + N, то есть [N]_обр = 1,1111 + N.

Обобщая результаты, получим:

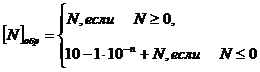
Дополнительный код числа N – [N]_доп.

- если N<=0, то [N]_доп = [N]_пр = 0, a₁ a₂ a₃ … a_m;

- если N>=0, то [N]_доп = 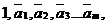+0,0 0…1.

Дополнительный код положительного числа совпадает с прямым кодом. Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы нулями) и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд, к числу следует прибавить единицу в младший разряд.

Например, число N = 0,1011, [N]_доп = 0,1011.

Число N = - 0,1011, [N]_доп = 1,0100. N = 0,0000; [N]_доп = 10,0000 = 0,0000 (1 исчезает). Неоднозначности в изображении 0 нет.

Выполнение арифметических операций.Сложение двоичных чисел производится поразрядно на основании следующих правил:

(0)+(0)=(0) (0)+(1)=(1) (1)+(0)=1 (1)+(1)=(10)

результат последнего выражения (0), а (1) переносится в следующий разряд.

Вычитание также производится по разрядам от младшего к старшему. При этом если из (0) вычитают (1), то результатом в этом разряде будет (1), а из следующего старшего разряда произойдет заем (1), т.е. цифра этого разряда станет на (1) меньше. Рассмотрим пример выполнения этих операций.

Сложение100101Вычитание100101

+ -

001011 001011

Результат110000Результат011010

Умножение двоичных чисел производится аналогично умножению десятичных с учетом следующих соотношений:

(0)x(0)=0 (0)x(1)=0 (1)x(0)=0 (1)x(1)=1

Множимое последовательно умножают на каждую цифру множителя, начиная с младшего разряда, и для учета веса соответствующей цифры множителя сдвигают влево на такое количество разрядов, на какое соответствующий разряд множителя сдвинут относительно младшего или старшего разряда.

х

-----

+

-------

Выполнение арифметических операций с использованием дополнительного кода.Рассмотрим пример сложения двух двоичных чисел, одно из которых является отрицательным числом. В этом случае, при использовании дополнительного кода, возможно заменить операцию вычитания операцией сложения. Например, при вычитании из числа 10110₂ (22₁₀) числа 01101₂ (13₁₀) уменьшаемое представляют в прямом коде 010110 (записывают впереди 0 как символ, обозначающий положительный знак числа). Вычитаемое представляют в дополнительном коде, сначала инвертировав цифры всех разрядов, кроме знакового (110010), а затем прибавляют единицу в младший разряд (110011). После этого выполняется операция сложения уменьшаемого (записанного в прямом коде) и вычитаемого (записанного в обратном коде).

010110

+

110011

---------

001001 (+9₁₀ = 22₁₀ - 13₁₀)

При сложении цифры знаковых разрядов складываются с отбрасыванием возникающего из этого разряда переноса. При умножении двоичных цифр с учетом их знаков необходимо получить две величины – определить знак произведения и найти абсолютную величину произведения. Знаковый разряд произведения получается суммированием цифр знаковых разрядов сомножителей по модулю 2, т.е.без формирования разряда переноса. При несовпадении складываемых цифр получается 1, что соответствует знаку произведения сомножителей, одно из которых меньше нуля. Абсолютная величина произведения определяется перемножением чисел без учета их знаковых разрядов.

3. Задания для выполнения практической работы. Для заданий 3.1-3.4 исходные данные приведены в таблице 1.3.

3.1. Произвести последовательный перевод целого числа из десятичной системы счисления в системы счисления с основаниями, заданными степенями числа 2. Системы счисления определяются вариантом задания. Произвести обратный перевод в десятичную систему счисления.

3.2. Произвести перевод дробного числа из десятичной системы счисления в системы счисления с основанием, заданными степенями числа 2. При иррациональном представлении числа использовать первые десять разрядов. Системы счисления определяются вариантом задания. Произвести обратный перевод в десятичную систему счисления. Оценить относительную точность перевода.

3.3. Произвести перевод целого числа из десятичной системы счисления в систему счисления, определенную вариантом задания. Произвести обратный перевод в десятичную систему счисления.

3.4. Произвести перевод дробного числа из десятичной системы счисления в систему счисления, определенную вариантом задания. При иррациональном представлении числа использовать первые десять разрядов. Система счисления определяется вариантом задания. Произвести обратный перевод в десятичную систему счисления. Оценить относительную точность перевода.

Оформление работы должно отражать и иллюстрировать принципы перевода чисел из одной системы счисления в другую.

Например: 1000₁₀ / 2 = 500 (0) / 2 = 250 (0) / 2 = 125 (0) / 2 = 62 (1) / 2 = 31 (0) / 2 = 15 (1) / 2 = 7 (1) / 2 = 3 (1) / 2 = 1 (1) / 2 = 0 (1).

Таким образом: 1000₁₀ = 1111101000₂

1111101000₂ → 11 1110 1000₂ → 0011 1110 1000₂ → 3Е8₁₆

1111101000₂ Х = 1 * 2⁹ + 1 * 2⁸ + 1 * 2⁷ + 1 * 2⁶ + 1 * 2⁵ + 0 * 2⁴ + 1 * 2³ + 0 * 2² + 0 * 2¹ + 0 * 2⁰ = 1000₁₀

Для заданий 3.5-3.12 исходные данные приведены в таблице 1.4.

3.5. Получить прямой код числа.

3.6. Получить обратный код числа.

3.7. Получить дополнительный код числа.

3.8. Выполнить операцию сложения двоичных чисел.

3.9. Выполнить операцию вычитания двоичных чисел.

3.10. Выполнить операцию умножения двоичных чисел.

3.11. Выполнить операцию вычитания двоичных чисел с использованием дополнительного кода.

3.12. Выполнить операцию умножения знаковых двоичных чисел.

Оформление работы должно отражать и иллюстрировать принципы выполнения заданий.

4. Варианты заданий для практической работы.

Таблица 1.3. Варианты заданий.

№	Целое число	Дробное число	Основания систем (для задания 3.1)	Основания систем (для задания 3.2)	Основание системы (для задания 3.3)	Основание системы (для задания 3.4)
		0,34341	10-2-16-10	10-2-16-10
		0,66611	10-8-2-10	10-8-2-10
		0,98834	10-16-8-10	10-16-8-10
		0,68510	10-16-2-10	10-16-2-10
		0,22287	10-2-8-10	10-2-8-10
		0,80740	10-8-16-10	10-8-16-10
		0,87979	10-2-16-10	10-2-16-10
		0,78824	10-8-2-10	10-8-2-10
		0,49300	10-16-8-10	10-16-8-10
		0,43331	10-16-2-10	10-16-2-10
		0,90212	10-2-8-10	10-2-8-10
		0,87985	10-8-16-10	10-8-16-10
		0,34430	10-2-16-10	10-2-16-10
		0,65620	10-8-2-10	10-8-2-10
		0,35305	10-16-8-10	10-16-8-10
		0,51145	10-16-2-10	10-16-2-10
		0,58419	10-2-8-10	10-2-8-10
		0,38867	10-8-16-10	10-8-16-10
		0,22670	10-2-16-10	10-2-16-10
		0,22287	10-2-8-10	10-2-8-10
		0,80740	10-8-16-10	10-8-16-10
		0,87979	10-2-16-10	10-2-16-10
		0,78824	10-8-2-10	10-8-2-10
		0,49300	10-16-8-10	10-16-8-10
		0,43331	10-16-2-10	10-16-2-10
		0,90212	10-2-8-10	10-2-8-10
		0,87985	10-8-16-10	10-8-16-10
		0,34430	10-2-16-10	10-2-16-10
		0,65620	10-8-2-10	10-8-2-10
		0,76804	10-8-2-10	10-8-2-10

Таблица 1.4. Варианты заданий.

№ п/п	3.5	3.6	3.7	3.8	3.9	3.10	3.11	3.12
		11001	11001					10010 01001
		10001	10001					11001 00001
		10010	10010					00101 10010
		10000	10000					10111 00000
		11011	11011					00001 11011
		10001	10001					00010 10001
		11011	11011					11001 01011
		11110	11110					01100 11110
		10000	10000					10101 00000
		10111	10111					00010 10111
		10001	10001					10001 00001
		10111	10111					01001 10111
		10010	10010					10110 00010
		10010	10010					01001 10010
		10000	10111					00111 10000
		10011	10111					10011 00111
		10010	10010					10111 00010
		11101	11101					01011 11101
		10111	10111					00010 10111
		10001	10001					10001 00001
		10111	10111					01001 10111
		10010	10010					10110 00010
		10010	10010					01001 10010
		10000	10111					00111 10000
		10011	10111					10011 00111
		10010	10010					10111 00010
		11101	11101					01011 11101
		10111	10011					10011 00111
		10001	10001					10001 00001
		10111	10011					10011 00111

5. Контрольные вопросы.

1. Что такое система счисления?
2. Что называется основанием системы счисления?
3. Приведите правила перевода чисел из десятичной системы счисления в двоичную.
4. Приведите правила перевода чисел из восьмеричной системы счисления в двоичную.
5. Приведите правила перевода чисел из двоичной системы счисления в шестнадцатеричную.
6. Что называется прямым кодом числа?
7. Что называется обратным кодом числа?
8. Что называется дополнительным кодом числа?
9. Приведите правила сложения двоичных чисел.
10. Приведите правила вычитания двоичных чисел.
11. Приведите правила умножения двоичных чисел.
12. Приведите правила вычитания двоичных чисел с использованием дополнительного кода.
13. Приведите правила умножения двоичных чисел с использованием дополнительного кода.