Численное решение задачи Коши
Теоретическая часть
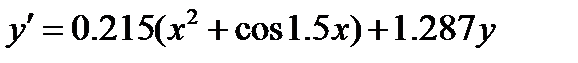
Метод Эйлера.Решить задачу Коши
c начальным условием x0=0.2 , y0=0.25
| A | B | C | D | E | F | G | |
| x0= | 0,2 | h= | 0,1 | y0= | 0.25 | ||
| i | xi | y=f(xi;xi) | dy=h*y | ||||
| =C3 | =G3 | =$E$3*(0,215*(D5^2+COS(1,5*D5))+1,287*E5) | |||||
| =D5+$E$3 | =E5+F5 | =$E$3*(0,215*(D6^2+COS(1,5*D6))+1,287*E6) | |||||
| =D6+$E$3 | =E6+F6 | =$E$3*(0,215*(D7^2+COS(1,5*D7))+1,287*E7) | |||||
| =D7+$E$3 | =E7+F7 | =$E$3*(0,215*(D8^2+COS(1,5*D8))+1,287*E8) | |||||
| =D8+$E$3 | =E8+F8 | =$E$3*(0,215*(D9^2+COS(1,5*D9))+1,287*E9) | |||||
| =D9+$E$3 | =E9+F9 | =$E$3*(0,215*(D10^2+COS(1,5*D10))+1,287*E10) | |||||
| =D10+$E$3 | =E10+F10 | =$E$3*(0,215*(D11^2+COS(1,5*D11))+1,287*E11) |
Результат:
| x0= | 0,2 | h= | 0,1 | y0= | 0,25 |
| i | xi | y=f(xi;xi) | dy=h*y | ||
| 0,2 | 0,25 | 0,053575 | |||
| 0,3 | 0,303575 | 0,060365 | |||
| 0,4 | 0,363939 | 0,068024 | |||
| 0,5 | 0,431963 | 0,0767 | |||
| 0,6 | 0,508663 | 0,08657 | |||
| 0,7 | 0,595233 | 0,097839 | |||
| 0,8 | 0,693072 | 0,110749 | |||
| 0,9 | 0,803821 | 0,125575 | |||
| 0,929396 | 0,142634 | ||||
| 1,1 | 1,07203 | 0,162284 | |||
| 1,2 | 1,234315 | 0,184931 | |||
| 1,3 | 1,419246 | 0,211033 | |||
| 1,4 | 1,630279 | 0,241103 | |||
| 1,5 | 1,871382 | 0,275716 | |||
| 1,6 | 2,147098 | 0,315518 | |||
| 1,7 | 2,462616 | 0,361227 | |||
| 1,8 | 2,823843 | 0,413651 | |||
| 1,9 | 3,237494 | 0,473688 | |||
| 3,711182 | 0,542344 | ||||
| 2,1 | 4,253527 | 0,620745 | |||
| 2,2 | 4,874271 | 0,710148 | |||
| 2,3 | 5,584419 | 0,811964 | |||
| 2,4 | 6,396383 | 0,927774 |
I= 6,397.
Алгоритм решения в TMTPascal.
Задача. Численно решить задачу Коши для обыкновенного дифферен-циального уравнения 1-го порядка
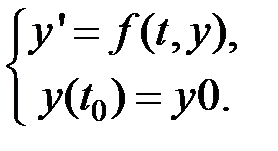
на отрезке 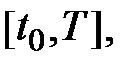 с шагом
с шагом 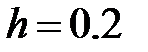 методом Эйлера. Найти точное решение задачи.
методом Эйлера. Найти точное решение задачи.
| № | f(t,y) | t0 | T | y0 |
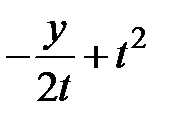 |
Решение.
program metod_Euler;
var a,b,t0,y0,t1,y1,h,e,dy,d:real;
n,k,i:integer;
function ff(y,t:real):real;
begin ff:=-y/(2*t)+t*t end;
begin
clrscr;
write('a=');
readln(a);
write('b=');
readln(b);
write('t0=');
readln(t0);write('y0=');
readln(y0);write('n=');
readln(n);k:=0;h:=(b-a)/n;
dy:=h*ff(t0,y0);
for i:=1 to n do begin
t1:=t0+h;
y1:=y0+dy;
k:=k+1;
dy:=h*ff(t1,y1);
write('k=',k:2);write(' t=',t1:7:4);
write(' y=',y1:7:4);write(' dy=',dy:7:4);
d:=abs(y1-y0);
writeln(' d=',d:7:3);
t0:=t1;y0=y1;
end;
readln;end.
Результат:
. 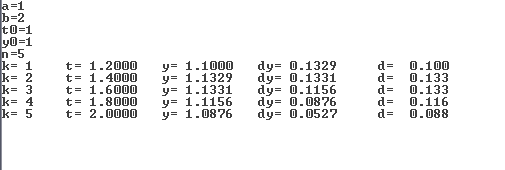
Метод Рунге-Кутта 4-го порядка. Особо широко известно вычислительное правило Рунге-Кутта четвертого порядка точности: 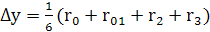 , где
, где
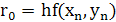 ,
,
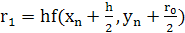 ,
,
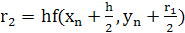 ,
,
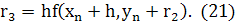
Метод Рунге-Кутта имеет погрешность четвертого порядка (~h4).
Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно оценить по формуле: 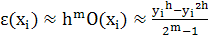 .(22)
.(22)
В формуле O(xi) – главный член погрешности, 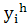 и
и 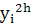 - приближенные решения в точке xi, найденные с шагом h и 2h соответственно.
- приближенные решения в точке xi, найденные с шагом h и 2h соответственно.
Алгоритм решения дифференциальных уравнений методом Рунге-Кутта.
Задача. Рассмотрим пример. Решить дифференциальное уравнение
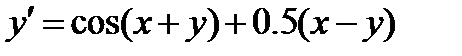
у0=0, х0=0 на отрезке [0,1] с шагом 0.1 методом Рунге-Кутта 4-го порядка.
Решение. Воспользуемся формулами (21), (22), построим таблицу
| A | B | C | D | E | F | |
| h= | 0,1 | |||||
| i | xi | yi | xi+h/2 | k1 | yi+k1/2 | |
| =C6+$D$3/2 | =$D$3*(COS(C6+D6)+0,5*(C6-D6)) | =D6+F6/2 | ||||
| =C6+$D$3 | =D6+N6 | =C7+$D$3/2 | =$D$3*(COS(C7+D7)+0,5*(C7-D7)) | =D7+F7/2 | ||
| =C7+$D$3 | =D7+N7 | =C8+$D$3/2 | =$D$3*(COS(C8+D8)+0,5*(C8-D8)) | =D8+F8/2 | ||
| =C8+$D$3 | =D8+N8 | =C9+$D$3/2 | =$D$3*(COS(C9+D9)+0,5*(C9-D9)) | =D9+F9/2 |
…… …….. ……… ………………………….. ……
| G | H | I |
| k2 | Yk+K2/2 | K3 |
| =$D$3*(COS(E6+G6)+0,5*(E6-G6)) | =D6+$H$6/2 | =$D$3*(COS(E6+I6)+0,5*(E6-I6)) |
| =$D$3*(COS(E7+G7)+0,5*(E7-G7)) | =D7+$H$6/2 | =$D$3*(COS(E7+I7)+0,5*(E7-I7)) |
| =$D$3*(COS(E8+G8)+0,5*(E8-G8)) | =D8+$H$6/2 | =$D$3*(COS(E8+I8)+0,5*(E8-I8)) |
| =$D$3*(COS(E9+G9)+0,5*(E9-G9)) | =D9+$H$6/2 | =$D$3*(COS(E9+I9)+0,5*(E9-I9)) |
……………………………… ……………. ……………………………….
| J | K | L | M |
| Xi+h | Yi+K3 | K4 | dy |
| =C6+$D$3 | =D6+J6 | =$D$3*(COS(K6+L6)+0,5*(K6-L6)) | =1/6*(F6+2*H6+2*J6+M6) |
| =C7+$D$3 | =D7+J7 | =$D$3*(COS(K7+L7)+0,5*(K7-L7)) | =1/6*(F7+2*H7+2*J7+M7) |
| =C8+$D$3 | =D8+J8 | =$D$3*(COS(K8+L8)+0,5*(K8-L8)) | =1/6*(F8+2*H8+2*J8+M8) |
| =C9+$D$3 | =D9+J9 | =$D$3*(COS(K9+L9)+0,5*(K9-L9)) | =1/6*(F9+2*H9+2*J9+M9) |
………. …….. ………………………….. ………………………….
Результат
| C | D | E | F | G | H | I | J | K | L | M | N | |||||||
| Метод Рунге - Кутта | ||||||||||||||||||
| h= | 0,1 | |||||||||||||||||
| i | xi | yi | xi+h/2 | k1 | yi+k1/2 | k2 | Yk+K2/2 | K3 | Xi+h | Yi+K3 | K4 | dy | ||||||
| 0 | 0,05 | 0,1 | 0,05 | 0,0995 | 0,0497 | 0,0995 | 0,1 | 0,0995 | 0,0980 | 0,0993 | ||||||||
| 0,1 | 0,0993 | 0,15 | 0,0980 | 0,14836 | 0,0956 | 0,1490 | 0,0955 | 0,2 | 0,1949 | 0,0925 | 0,0955 | |||||||
| 0,2 | 0,1948 | 0,25 | 0,0925 | 0,24113 | 0,0886 | 0,2446 | 0,0880 | 0,3 | 0,2828 | 0,0843 | 0,0883 | |||||||
| 0,3 | 0,2832 | 0,35 | 0,0843 | 0,3253 | 0,0792 | 0,3329 | 0,0776 | 0,4 | 0,3608 | 0,0743 | 0,0787 | |||||||
| 0,4 | 0,3619 | 0,45 | 0,0742 | 0,39910 | 0,068 | 0,4117 | 0,0653 | 0,5 | 0,4272 | 0,0636 | 0,0676 | |||||||
| 0,5 | 0,4296 | 0,55 | 0,0633 | 0,46127 | 0,0575 | 0,4793 | 0,0518 | 0,6 | 0,4814 | 0,0529 | 0,0558 | |||||||
| 0,6 | 0,4854 | 0,65 | 0,0523 | 0,51163 | 0,0467 | 0,5351 | 0,0381 | 0,7 | 0,5236 | 0,0428 | 0,0441 | |||||||
| 0,7 | 0,5296 | 0,75 | 0,0419 | 0,55060 | 0,0366 | 0,5793 | 0,0247 | 0,8 | 0,5543 | 0,0337 | 0,0330 | |||||||
| 0,8 | 0,5627 | 0,85 | 0,0325 | 0,57897 | 0,0276 | 0,6124 | 0,012 | 0,9 | 0,5747 | 0,0258 | 0,0229 | |||||||
| 0,9 | 0,585 | 0,95 | 0,0242 | 0,59778 | 0,0199 | 0,6354 | 0,0001 | 0,5857 | 0,0192 | 0,0139 | ||||||||
y=0,585.
Алгоритм решения задачи Коши методом Рунге-Кутта на языке TMTPascal.
program metod_Runge_Kutta;
var { решение дифф-ных уравнений }
a,b,h,x,y,y0,x0,k1,k2,k3,k4:real; { методом Рунге-Кутта }
i,n:integer;
function FF(x,y:real):real; { исходная функция для определения }
begin { коэфф-тов k1,k2,k3,k4 }
FF:=cos(x+y)+0.5*(x-y);
end;
function f1(y,k1,k2,k3,k4:real):real; { функция для построения таблицы }
begin { приближенных решений данного }
f1:=y+(h/6)*(k1+2*k2+2*k3+k4); { дифф-ного уравнения }
end;
begin
write('введите величину шага h= ');
readln(h);
Write('введите начало интервала a= ');
readln(a);
{Write('введите конец интервала b= ');
readln(b);}
write('введите y(a)= ');
readln(y0);
n:=10; { количество приближенных решений в нашей таблице }
x0:=a;
for i:=1 to n do
begin
k1:=FF(x,y);
k2:=FF(x+h/2,y+(k1*h)/2);
k3:=FF(x+h/2,y+(h*k2)/2);
k4:=FF(x+h,y+(h*k3));
y:=f1(y,k1,k2,k3,k4);
writeln(' Y[',i,'] = ',y:2:4); { вывод таблицы приближенных решений }
x:=x0+i*h;
End;
end.
Практическая часть
Задание 1. Численно решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка
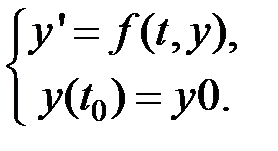
на отрезке 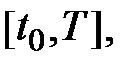 с шагом
с шагом 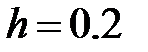 а) методом Эйлера; б) методом Рунге-Кутта 2-го порядка с оценкой погрешности по правилу Рунге.
а) методом Эйлера; б) методом Рунге-Кутта 2-го порядка с оценкой погрешности по правилу Рунге.
Найти точное решение задачи.
| № | f(t,y) | t0 | T | y0 | № | f(t,y) | t0 | T | y0 |
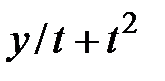 | 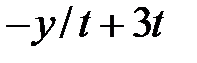 | ||||||||
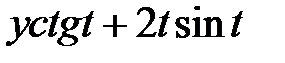 | 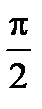 | 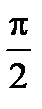 +1 +1 | 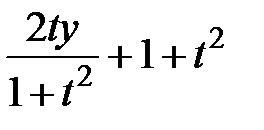 | ||||||
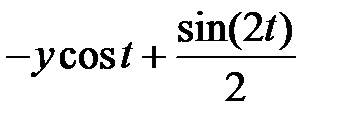 | 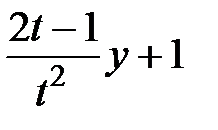 | ||||||||
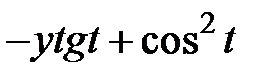 | 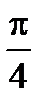 | 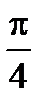 +1 +1 | 0.5 | 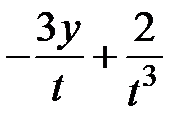 | |||||
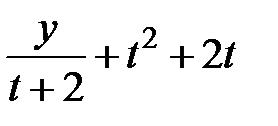 | -1 | 1.5 | 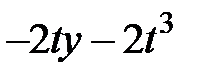 | 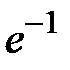 | |||||
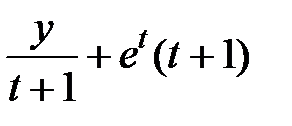 | 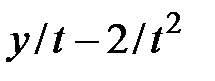 | ||||||||
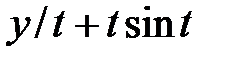 | 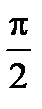 | 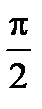 +1 +1 | 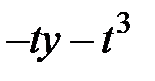 | ||||||
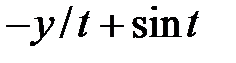 | p | p+1 | 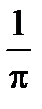 | 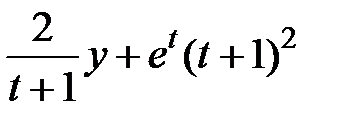 | |||||
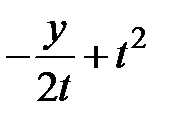 | 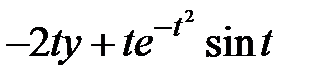 | ||||||||
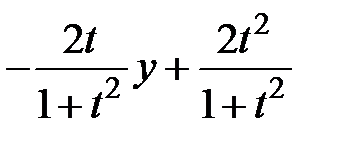 | 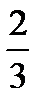 | 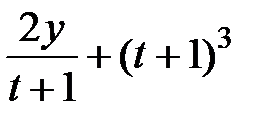 | 0.5 | ||||||
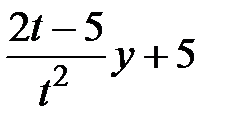 | 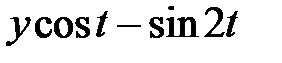 | ||||||||
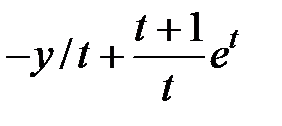 |  | 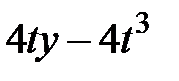 | -0.5 | ||||||
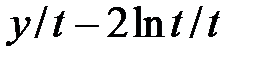 | 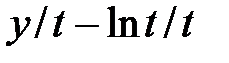 | ||||||||
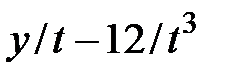 | 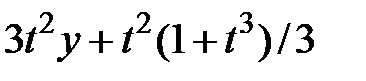 | ||||||||
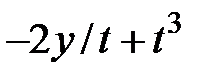 | - 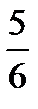 | 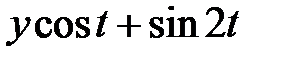 | -1 |
Вопросы к защите лабораторной работы № 6
«Численное решение задачи Коши»
1. Постановка задачи Коши. Дискретная задача Коши: основные понятия и определения (сетка, сеточные функции, численный метод, аппроксимация, сходимость).
2. Численные методы решения задачи Коши: вывод формулы метода Эйлера, его геометрическая интерпретация, устойчивость, оценка погрешности, влияние вычислительной погрешности.
3. Методы Рунге-Кутты. Вывод формул. Оценка погрешности.
СПИСОК ЛИТЕРАТУРЫ
1. Боглаев, Ю.П. Вычислительная математика и программирование./ Ю.П. Боглаев -М.: Высшая школа, 1990.-246с.
2. Додж, М. Эффективная работа в Microsoft Excel 2000./ М. Додж, К.Стинсон. - СПб.: Питер, 2002. - 1056 с.
3. Заварыкин, В.М. Численные методы: Учеб. пособие для студ. Физ.- мат. Спец. пед. ин-тов./ В.М. Заварыкин, В.Г. Житомирский,М.П. Лапчик -М.:Просвещение,1990.- 176с.
4. Исаков, В.Н. Элементы численных методов. Учеб. пособие для студ. высш. пед. учеб. заведений./ В.Н. Исаков - М.: Изд. Центр «Академия»,2003. - 192с.
5. Лапчик, М.П. Численные методы: Учебное пособие для студ. вузов./ М.П. Лапчик, М.И. Рагулина, Е.К. Хеннер. - М.:Академия,2005.-384с.
6. Могилев, А.В. Информатика: Учеб. пособие для студ. пед. вузов./ А.В. Могилев, Н.И. Пак, Е.К. Хеннер; под ред. Е.К. Хеннера. – М.: Изд. Центр «Академия», 2000. – 816 с.
7. Пирумов, У.Г. Численные методы: учеб. пособие для студ. вузов./ У.Г. Пирумов. - М.: Дрофа,2004. - 224с.
Автор составитель:
Кормилицына Татьяна Владимировна
Научно-методическое издание
ЧИСЛЕННЫЕ МЕТОДЫ
методические материалы к лабораторным работам
Редактор
Корректор
Компьютерная верстка Т.В.Кормилицыной, И.А.Козловой
Подписано в печать
Формат 60х84 1/16. Печать ризография. Гарнитура «Times New Roman ».
Усл.-печ.л.2,5. Уч.-изд. л. 2,7.
Тираж . Заказ №
ГОУ ВПО «Мордовский государственный педагогический институт
имени М.Е.Евсевьева»
Лаборатория множительной техники
430007, г. Саранск, ул. Студенческая, 11а
