Метод Гаусса по схеме единственного деления.
Задача. Решить систему уравнений по схеме единственного деления:
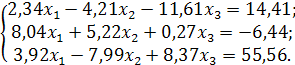
Решение осуществим с помощью формул (9) и (10):
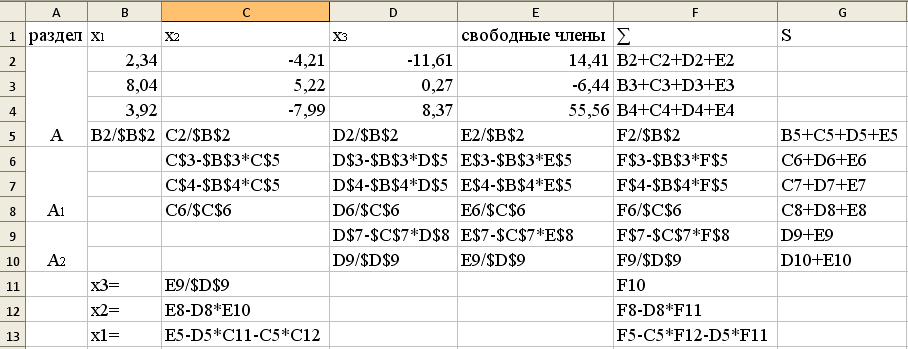
Результат:
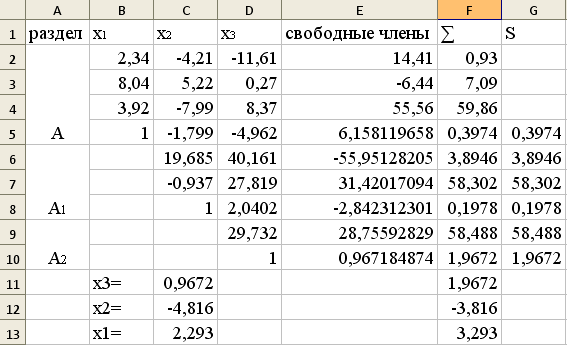
Решение системы: x1=2,293021, x2=-4,81552, x3=0,967185.
Схема полного деления.
Задача. Решить систему уравнений по схеме полного деления:
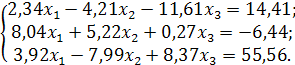
Решение:
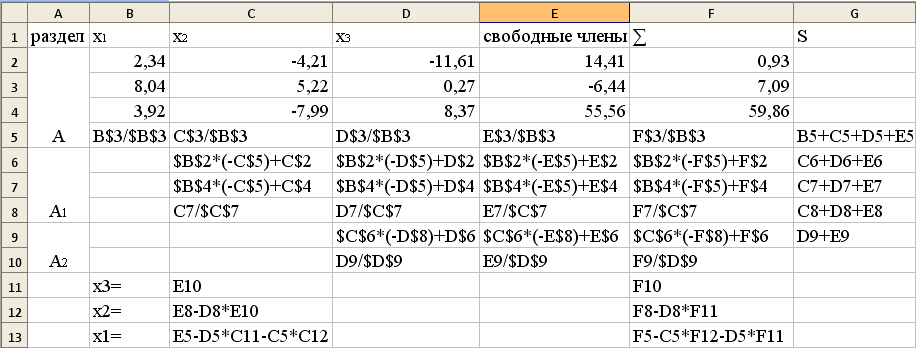
Результат:
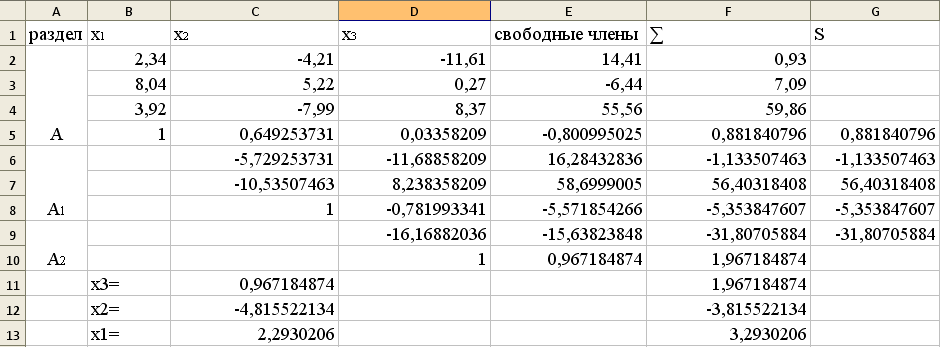
Решение системы: x1=2,2930206,x2=-4,815522134,x3=0,967184874.
Методом Зейделя
Задача. Решить систему уравнений методом Зейделя:
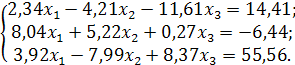
Решение. Воспользуемся формулами (11), (12) и (13):
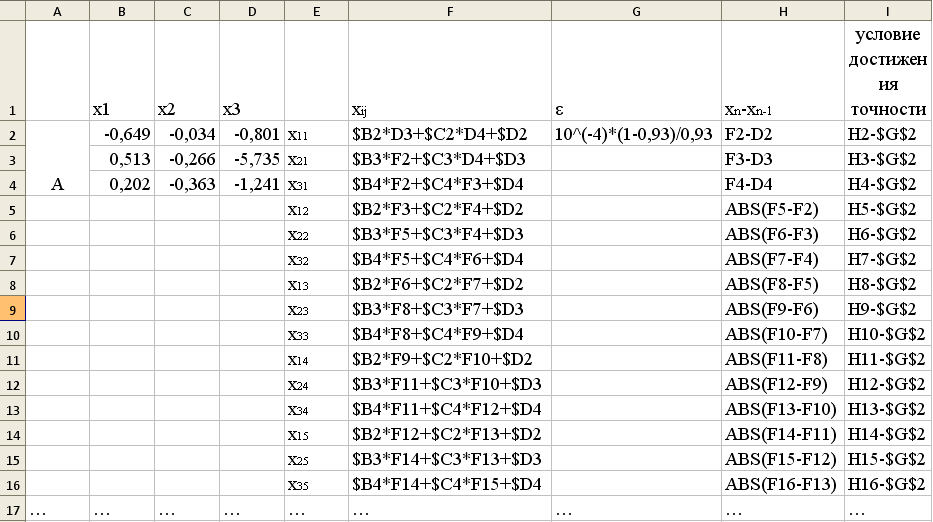
Результат:
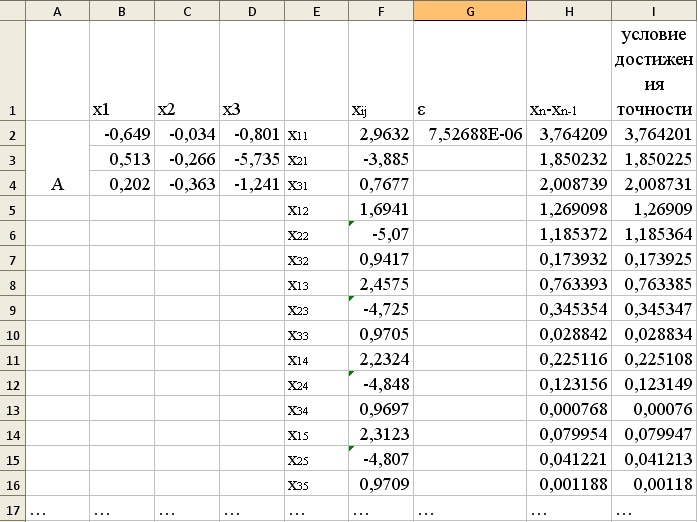
Решение системы: x1≈2,232388,x2≈-4,84794,x3≈0,969745.
Решение достигается более чем за 14 итераций, т.е. трудоемко и занимает много времени.
Задача. Решить методом итераций СЛАУ, оценив предварительно гарантированное количество итераций. Точность 0,001
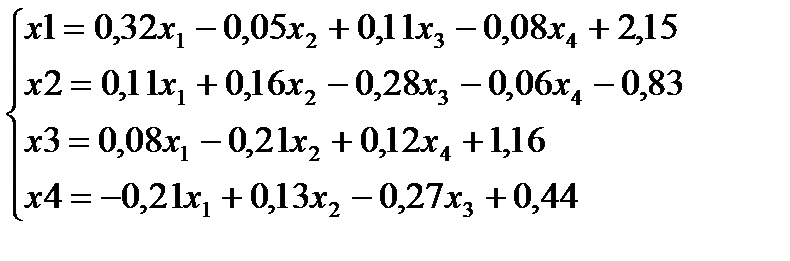
Решение.
Для применения метода итераций с заданной точностью ε применим оценку
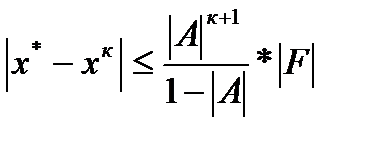 ,
,
где А константа из формул критерия сходимости итерационного процесса
F-мах[|b1|,|b2|,|b3|]
Рассчитаем А по формуле |А|3= 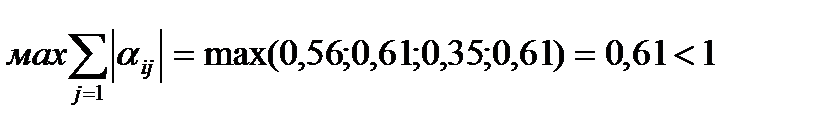

Значит, система имеет итерационный вид, т.е. можно построить последовательность решений по правой части исходной системы.
Если модуль |А|>1, то следует проверить формулу 4,5
Если формулы 3-5 не выполняются система не имеет итерационный вид, значит, метод итераций не применим, следует преобразовать исходную систему.
Вычислим |F|
|F|={2,15;0,83,1,16;0,44}=2,15=b1
Рассчитаем значение k (число итераций) с учётом точности ε=0,001
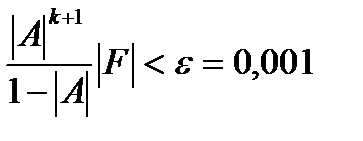
Заменим переменные их значениями
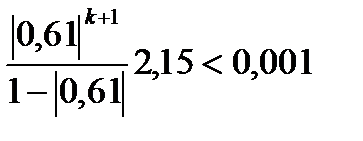 решим неравенство логарифмированием неравенства
решим неравенство логарифмированием неравенства
lg(0,61k+1)-lg(0,39)+lg(2,15)<lg10-3
(k+1)*lg(0,61)<lg(0,39)+3-lg(2,15)
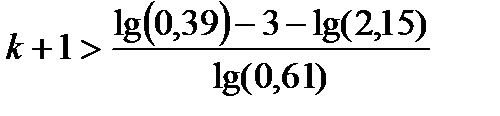
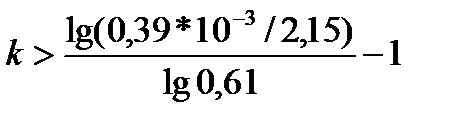
k=k-1 k>17,5-1, к>17
Вывод: для достижения заданной точности требуется выполнять по максимуму 17 итераций, на практике сходимость достигается раньше.
Алгоритм решения системы линейных уравнений в TMTPascal:
1) Метод итераций. Предварительно система должна быть приведена к итерационному виду.
program Iter_sys;
const
a11=0.24; a12=0.21; a13=0.06; a14=-0.34;
a21=0.05; a22=0; a23=0.32; a24=0.12;
a31=0.35; a32=-0.27; a33=0; a34=-0.05;
a41=0.12; a42=-0.43; a43=0.34; a44=-0.21;
b1=1.42; b2=-0.57; b3=0.68; b4=-2.14;
var
x1,x2,x3,x4:real;
xx1,xx2,xx3,xx4:real;
i:integer;
begin
x1:=b1; x2:=b2; x3:=b3; x4:=b4;
for i:=1 to 104 do
begin
xx1:=a11*x1+a12*x2+a13*x3+a14*x4+b1;
xx2:=a21*x1+a22*x2+a23*x3+a24*x4+b2;
xx3:=a31*x1+a32*x2+a33*x3+a34*x4+b3;
xx4:=a41*x1+a42*x2+a43*x3+a44*x4+b4;
writeln(xx1:6:3, xx2:6:3, xx3:6:3, xx4:6:3);
x1:=xx1;
x2:=xx2;
x3:=XX3;
X4:=XX4;
END;
READLN;
END.
Результат:

2)Метод Зейделя. Предварительно система должна быть приведена к специальному виду:
program Zeydel_sys;
const
a11=0; a12=-0.949; a13=-0.511;
a21=-1.034; a22=0; a23=0.417;
a31=-0.533; a32=0.399; a33=0;
b1=0.2173; b2=-1.252; b3=-1.705;
var
x1,x2,x3:real;
xx1,xx2,xx3:real;
i:integer;
begin
x1:=b1; x2:=b2; x3:=b3;
for i:=1 to 30 do
begin
xx1:=-a12*x2-a13*x3+b1;
x1:=xx1;
xx2:=-a21*x1-a23*x3+b2;
x2:=xx2;
xx3:=-a31*x1-a32*x2+b3;
x3:=XX3;
writeln(xx1:6:3, xx2:6:3, xx3:6:3);
END;
READLN;
END.
Результат:
Практическая часть
Задание 1.Решить систему методом Гаусса, предварительно исследовать совместность.
Вариант 1 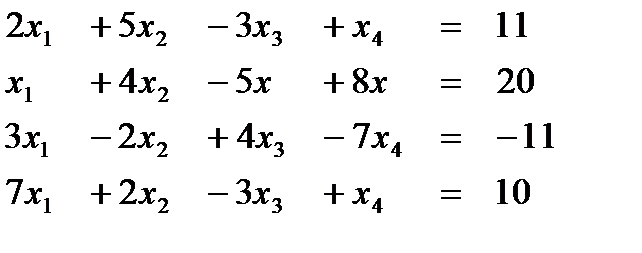 Ответ (1; 2; 1; 2) Ответ (1; 2; 1; 2) | Вариант 2 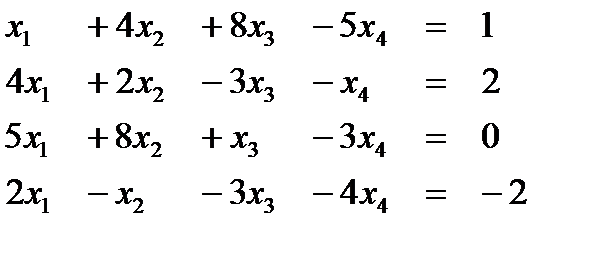 Ответ (2; -1; 1; 1) Ответ (2; -1; 1; 1) |
Вариант 3 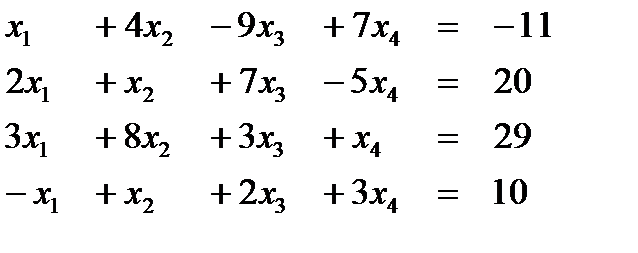 Ответ (1; 2; 3; 1) Ответ (1; 2; 3; 1) | Вариант 4 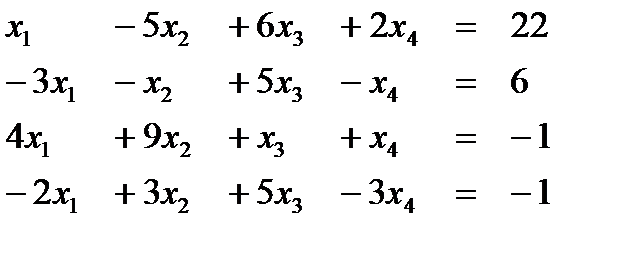 Ответ (1; -1; 2; 2) Ответ (1; -1; 2; 2) |
Вариант 5 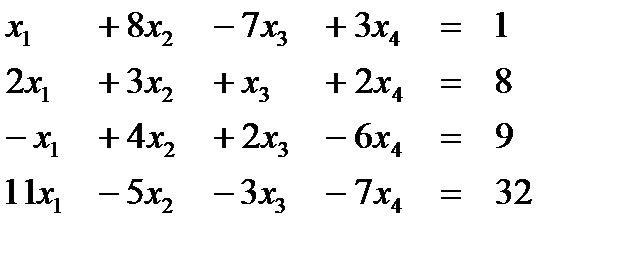 Ответ (3; 1; 1; -1) Ответ (3; 1; 1; -1) | Вариант 6 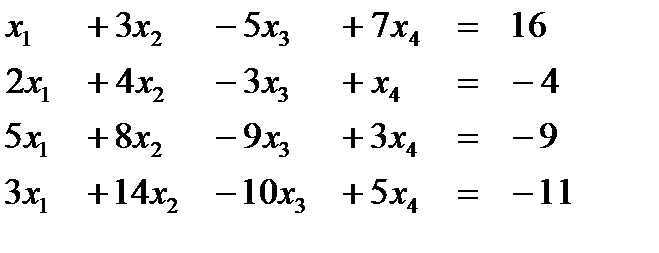 Ответ (1; -1; 2; 4) Ответ (1; -1; 2; 4) |
Вариант 7 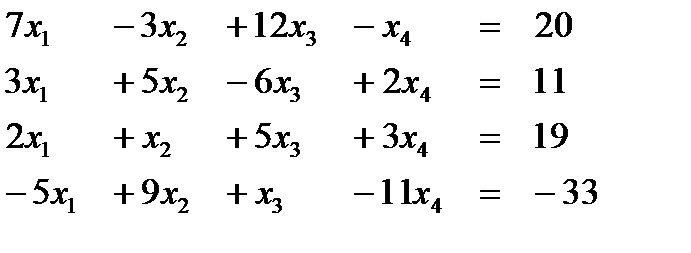 Ответ (2; 1; 1; 3) Ответ (2; 1; 1; 3) | Вариант 8 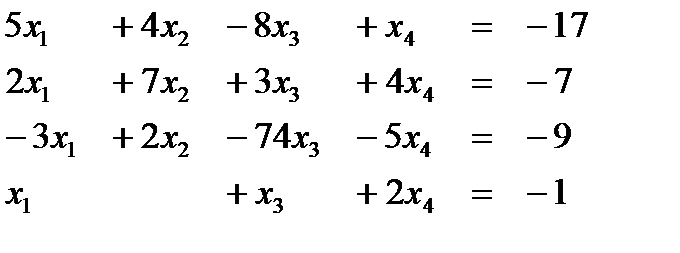 Ответ (1; -1; 2; -2) Ответ (1; -1; 2; -2) |
Вариант 9 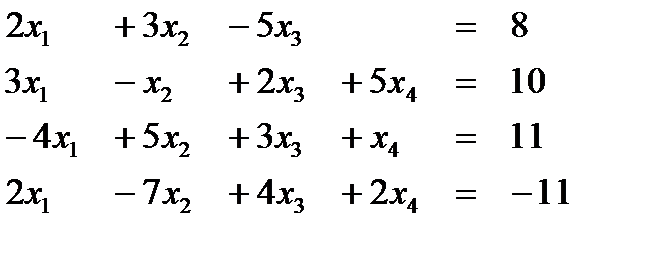 Ответ (2; 3; 1; 1) Ответ (2; 3; 1; 1) | Вариант 10 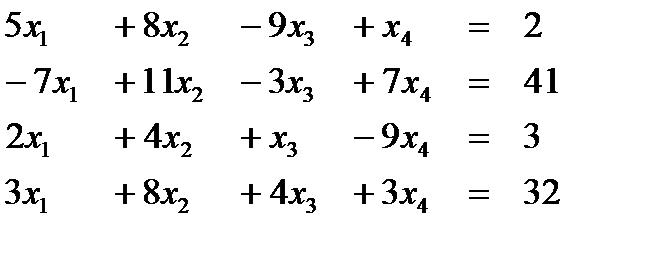 Ответ (-1; 3; 2; 1) Ответ (-1; 3; 2; 1) |
Вариант 11 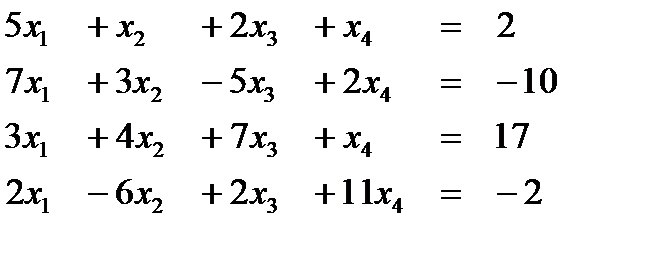 Ответ (-1; 1; 2; 2) Ответ (-1; 1; 2; 2) | Вариант 12 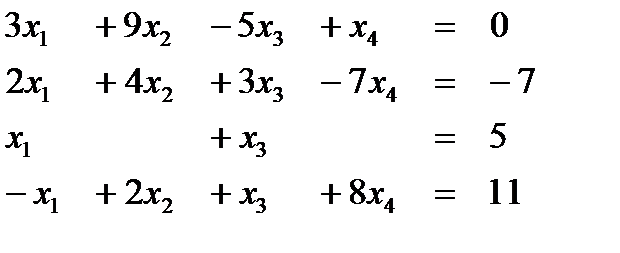 Ответ (4; -1; 1; 2) Ответ (4; -1; 1; 2) |
Вариант 13 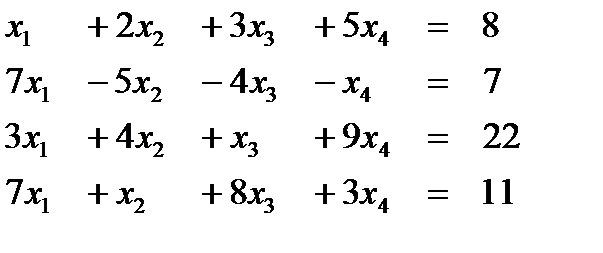 Ответ (2; 2; -1; 1) Ответ (2; 2; -1; 1) | Вариант 14 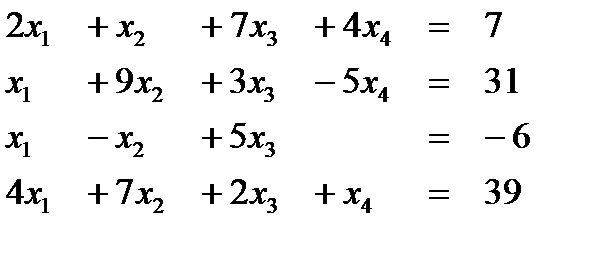 Ответ (3; 4; -1; 1) Ответ (3; 4; -1; 1) |
Вариант 15 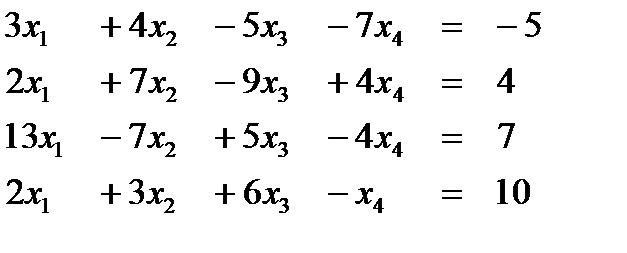 Ответ (1; 1; 1; 1) Ответ (1; 1; 1; 1) | Вариант 16 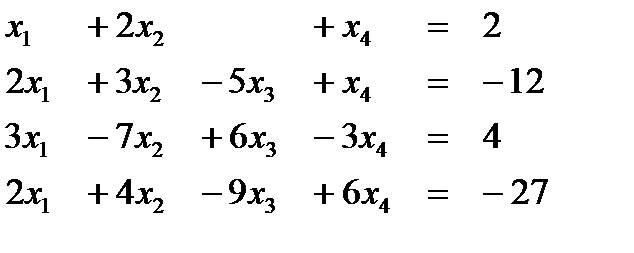 Ответ (-1; 2; 3; -1) Ответ (-1; 2; 3; -1) |
Задание 2. Решить систему из задания 1 методом Зейделя, предварительно приведя ее к специальному виду.
Вопросы к защите лабораторной работы №3
«Решение систем линейных алгебраических уравнений»
1. Метод Гаусса (схема единственного деления): описание метода, трудоемкость метода.
2. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора): описание метода, его вычислительная устойчивость.
3. Метод простой итерации (Якоби) для решения систем линейных алгебраических уравнений. Сходимость, оценки погрешности, критерий окончания итераций.
4. Метод Зейделя для решения систем линейных алгебраических уравнений. Сходимость, оценки погрешности, критерий окончания итераций. Геометрическая иллюстрация. Алгоритм приведения к виду, обеспечивающему сходимость итерационного процесса.
5. Как привести систему к виду, удобному для итераций по методу простой итерации и определить число итераций, требуемых для достижения точности 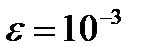 .
.
ЛАБОРАТОРНАЯ РАБОТА № 4
