Метод деления отрезка пополам (метод бисекции)

Министерство образования и науки РФ

ФГБОУ ВПО «Кубанский государственный технологический

Университет»

Кафедра электротехники и электрических машин

УТВЕРЖДАЮ
Заведующий кафедрой электротехники и электрических машин
к.т.н., доцент		ЯЯ.М. Кашин
____ _______ 2015 г.

Конспект лекций

По дисциплине «Численные методы расчета

Электрооборудования»

для студентов направления 13.04.02 «Электроэнергетика и электротехника»

Квалификация выпускника – магистр

Разработал:

к.т.н., доц. И.Н. Автайкин

Обсужден на заседании кафедры

электротехники и электрических машин

25 августа 2015 г. (протокол № 1)

Секретарь кафедры

к.т.н., доц. С.А. Попов

2015 г.

Лекция № 1 (2 часа)

По дисциплине «Численные методы расчета электрооборудования»

Тема № 1. Решение нелинейных уравнений

Цели: 1. Формирование следующих компетенций:

ОПК-2: Способностью применять современные методы исследования, оценивать и представлять результаты выполненной работы.

.

2. Формирование уровня обученности:

Знать: основные математические методы исследования электрооборудования.

Уметь: оценивать и анализировать результаты исследования.

Владеть: современными методами и математическими алгоритмами исследования электрооборудования.

Материальное обеспечение:

Учебные вопросы

1. Метод бисекции.

2. Метод секущих (хорд).

3. Метод простых итераций.

4. Метод Ньютона (касательных).

Литература

1. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы / Учебн. пособие- М.: Наука, 2011.- 631с.

2. Марчук Г.И. Методы вычислительной математики / Учебн. пособие- М.: Наука, 2011.- 535с.

Решение нелинейных уравнений

Пусть дано нелинейное уравнение вида:

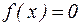, (1)

где 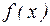- функция, определенная и непрерывная на некотором промежутке. Требуется найти корни уравнения, которые при подстановке в данное уравнение превращают его в числовое равенство.

Для решения данных уравнений применяют численные методы, которые являются приближенными с заданной степенью точности и состоят из двух этапов:

1. Находятся отрезки 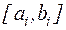, внутри которых содержится один корень 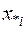. Этот этап называется отделением корней или локализацией корней. По сути, на данном этапе осуществляется грубое нахождение корней .

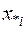2. Грубое значение каждого корня 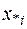уточняется до заданной точности одним из численных методов, в которых реализуется последовательные приближения.

Метод деления отрезка пополам (метод бисекции)

Допустим, что на отрезке [а,b], расположено искомое значение корня х=с, т. е. с ϵ [а,b]. В качестве начального приближения корня с₀ принимаем середину этого отрезка:

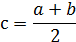
Далее исследуем значения функции F(x) на концах отрезков [а, с_о] и [с_о,b], т.е. в точках а, с_о, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; Допустим, что нам удалось найти отрезок [а,b], на котором расположено искомое значение корня поэтому его принимаем в качестве нового отрезка [a₁,b₁]. Вторую половину отрезка [а,b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка

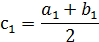
и т. д.

Таким образом, k-е приближение вычисляется как

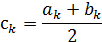
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k - итераций он сокращается в 2к раз:

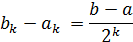
Иллюстрация данного метода приведена на рисунке 1.

Процесс вычислений завершается, когда длина текущего интервала становится меньше заданной величины точности - 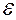нахождения корня.

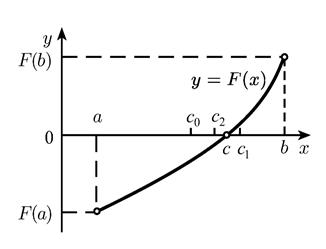
Рисунок 1 Графическая интерпретация нахождения корней

функции 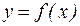методом бисекции

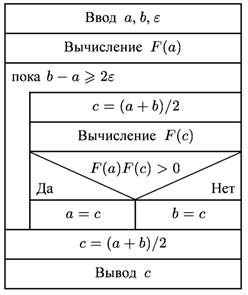
Рисунок 2 Алгоритм метода бисекции

Метод секущих (хорд)

Данный метод при одних и тех же начальных условиях обеспечивает более быстрое нахождение корня, чем метод бисекции. При использовании метода хорд отрезок [а,b], делится не пополам, а в отношении .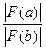

Геометрически метод хорд эквивалентен замене кривой 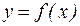хордой, проходящей через точк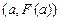и и 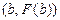, что иллюстрирует рисунок 3.

В аналитической геометрии выводится формула, задающая уравнение прямой, проходящей через две точки с координатами (х1; у1) и (х2; у2):

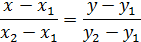
Подставляя значения 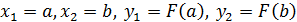получим уравнение хорды AB:

.

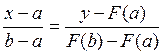Таким образом, первое приближение к корню, полученное методом секущих:

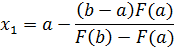
Теперь возьмем координаты x₁ и b и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид:

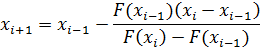
Повторять операцию следует до тех пор, пока x_i-x_i-1< 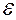не станет меньше или равно заданному значению погрешности.

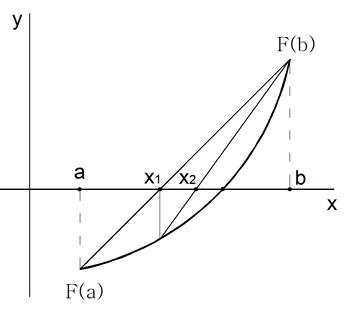
Рисунок 4 Графическая интерпретация нахождения корней

функции 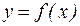методом хорд