Сопряженные комплексные числа. Свойства операции сопряжения.
Арифметические действия над комплексными числами.
Сопряженные комплексные числа. Свойства операции сопряжения.
Условимся в дальнейшем не делать различия между комплексным числом вида 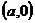 и действительным числом а, т. е.
и действительным числом а, т. е. 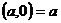 ; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
Рассмотрим упорядоченную пару 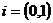 . Согласно закону умножения комплексных чисел, имеем
. Согласно закону умножения комплексных чисел, имеем 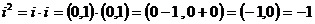 , тогда
, тогда 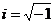 .
.
Определение 6. Упорядоченную пару 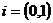 ,.удовлетворяющую
,.удовлетворяющую
соотношению 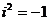 или
или  , называют мнимой единицей.
, называют мнимой единицей.
С помощью мнимой единицы можно выразить любое комплексное число. В самом деле, так как
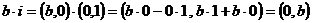 ,
,
то
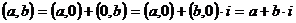 .
.
Теперь можно забыть о первоначальном способе задания комплексного числа как пары 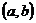 и записывать комплексное число в виде
и записывать комплексное число в виде 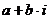 .
.
Определение 7. Выражение 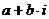 называют алгебраической формой
называют алгебраической формой
комплексного числа. Число а называют действительной частью,
число b – мнимой частью комплексного числа 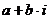 .
.
Если задано комплексное число 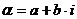 , то действительную часть числа
, то действительную часть числа 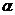 обозначают
обозначают 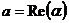 ( от франц. reele – «действительный»), а мнимую -
( от франц. reele – «действительный»), а мнимую - 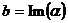 ( от франц. imaginaire – «мнимый»). Например,
( от франц. imaginaire – «мнимый»). Например, 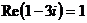 ,
, 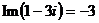 .
.
Если 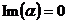 , то число
, то число 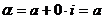 - действительное; если
- действительное; если 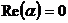 , то число
, то число 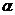 имеет вид
имеет вид 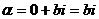 и называется чисто мнимым.
и называется чисто мнимым.
Определение 8.Пусть 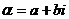 . Число
. Число 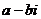 , отличающееся от
, отличающееся от 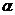 лишь
лишь
знаком коэффициента при мнимой части, называется
сопряженным числу 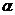 и обозначается
и обозначается 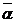 .
.
Итак, по определению, 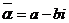 .
.
Если 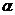 - действительное число, т.е.
- действительное число, т.е. 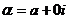 , то
, то 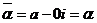 . Таким образом, любое действительное число равно своему сопряженному.
. Таким образом, любое действительное число равно своему сопряженному.
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами следует, что
1. 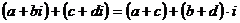 ,
,
2. 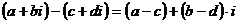 ,
,
3. 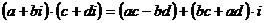 ,
,
4. 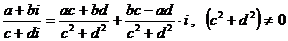 .
.
Формула 1 определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула 2 означает, что при вычитании одного комплексного числа из другого, необходимо вычесть отдельно их действительные и мнимые части.
Формулу 3 можно получить путем умножения по правилам алгебры и замены 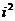 его значением:
его значением:
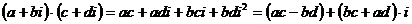 .
.
Чтобы получить формулу 4, необходимо предварительно числитель и знаменатель умножить на 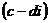 (число сопряженное числу
(число сопряженное числу 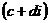 ):
): 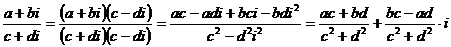 .
.
Сформулируем основные свойства операции сопряжения:
1) 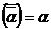 ; 4)
; 4) 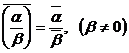 ;
;
2) 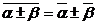 ; 5)
; 5) 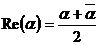 ;
;
3) 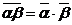 ; 6)
; 6) 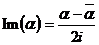 .
.
Упражнение 2. Доказать свойства 1-5 операции сопряжения.
Тригонометрическая форма комплексного числа и
Ее применение.
Формула Муавра.
Полагая в формулах (11) и (11*) 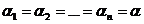 , получим
, получим
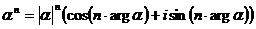 (12)
(12)
и
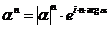 (12*)
(12*)
Формулы (12) и (12*) называются формулами Муавра.
Пример. Найти 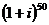 .
.
Решение. Представим число 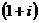 в тригонометрической форме и применим формулу Муавра:
в тригонометрической форме и применим формулу Муавра:
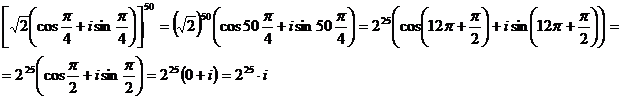
Для показательной формы имеем:
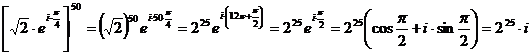 .
.
Следовательно, 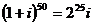 .
.
Арифметические действия над комплексными числами.
Сопряженные комплексные числа. Свойства операции сопряжения.
Условимся в дальнейшем не делать различия между комплексным числом вида 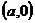 и действительным числом а, т. е.
и действительным числом а, т. е. 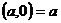 ; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
Рассмотрим упорядоченную пару 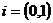 . Согласно закону умножения комплексных чисел, имеем
. Согласно закону умножения комплексных чисел, имеем 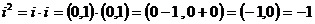 , тогда
, тогда 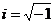 .
.
Определение 6. Упорядоченную пару 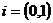 ,.удовлетворяющую
,.удовлетворяющую
соотношению 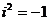 или
или  , называют мнимой единицей.
, называют мнимой единицей.
С помощью мнимой единицы можно выразить любое комплексное число. В самом деле, так как
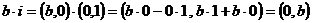 ,
,
то
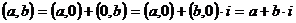 .
.
Теперь можно забыть о первоначальном способе задания комплексного числа как пары 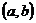 и записывать комплексное число в виде
и записывать комплексное число в виде 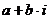 .
.
Определение 7. Выражение 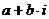 называют алгебраической формой
называют алгебраической формой
комплексного числа. Число а называют действительной частью,
число b – мнимой частью комплексного числа 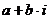 .
.
Если задано комплексное число 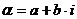 , то действительную часть числа
, то действительную часть числа 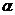 обозначают
обозначают 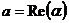 ( от франц. reele – «действительный»), а мнимую -
( от франц. reele – «действительный»), а мнимую - 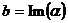 ( от франц. imaginaire – «мнимый»). Например,
( от франц. imaginaire – «мнимый»). Например, 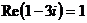 ,
, 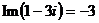 .
.
Если 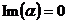 , то число
, то число 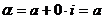 - действительное; если
- действительное; если 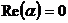 , то число
, то число 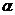 имеет вид
имеет вид 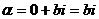 и называется чисто мнимым.
и называется чисто мнимым.
Определение 8.Пусть 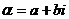 . Число
. Число 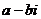 , отличающееся от
, отличающееся от 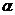 лишь
лишь
знаком коэффициента при мнимой части, называется
сопряженным числу 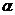 и обозначается
и обозначается 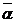 .
.
Итак, по определению, 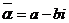 .
.
Если 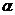 - действительное число, т.е.
- действительное число, т.е. 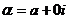 , то
, то 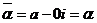 . Таким образом, любое действительное число равно своему сопряженному.
. Таким образом, любое действительное число равно своему сопряженному.
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами следует, что
1. 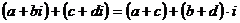 ,
,
2. 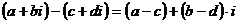 ,
,
3. 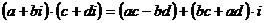 ,
,
4. 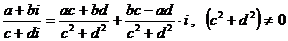 .
.
Формула 1 определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула 2 означает, что при вычитании одного комплексного числа из другого, необходимо вычесть отдельно их действительные и мнимые части.
Формулу 3 можно получить путем умножения по правилам алгебры и замены 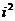 его значением:
его значением:
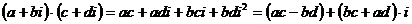 .
.
Чтобы получить формулу 4, необходимо предварительно числитель и знаменатель умножить на 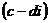 (число сопряженное числу
(число сопряженное числу 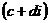 ):
): 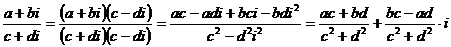 .
.
Сформулируем основные свойства операции сопряжения:
1) 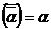 ; 4)
; 4) 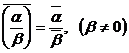 ;
;
2) 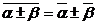 ; 5)
; 5) 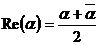 ;
;
3) 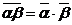 ; 6)
; 6) 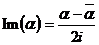 .
.
Упражнение 2. Доказать свойства 1-5 операции сопряжения.
