Курсовые работы по информатике

КУРСОВЫЕ РАБОТЫ ПО ИНФОРМАТИКЕ

Методические указания

к выполнению курсовых работ по курсу "Информатика"

для студентов всех специальностей и всех форм обучения

Составители:

кандидат технических наук, доцент Н. М. Третьякова

кандидат физико-математических наук, доцент М. Л. Герасин

Рецензент

кандидат физико-математических наук, доцент кафедры

математического моделирования и кибернетики

Сыктывкарского государственного университета Д. В. Холмогоров

ã Сыктывкарский государственный институт

Санкт-Петербургской государственной лесотехнической академии

им. С. М. Кирова, 1999

ВВЕДЕНИЕ

Изучение дисциплины «Информатика» предусматривает освоение теоретического курса, выполнение практических и лабораторных работ. Заключительным этапом обучения по данной дисциплине является выполнение курсового задания.

Основные цели курсового задания - практическое освоение всех этапов разработки и отладки программ, приобретение навыков, необходимых программисту для самостоятельной работы.

Задание по курсовой работе состоит из одной задачи, номер которой согласуется с преподавателем. Задачи в данных методических указаниях приведены в порядке возрастания их сложности (от раздела к разделу).

Выполнение работы включает в себя следующие этапы:

Анализ задачи.

Выбор метода решения задачи.

Разработка схемы алгоритма.

Составление программы на одном из языков программирования.

Отладка, тестирование и исполнение программы.

Составление пояснительной записки.

Результатом выполнения курсовой работы являются готовая программа объемом не менее 100 операторов и все необходимые пояснения к ней, оформленные в виде пояснительной записки (отчета).

Выполненная курсовая работа должна быть защищена. При выставлении оценки учитывается сложность задачи, качество разработанной программы, оформление пояснительной записки, степень самостоятельности студента при выполнении работы, а также знания, показанные студентом при работе над заданием и во время защиты.

Отчет о выполнении задания (пояснительная записка) должен содержать:

1. Титульный лист (см. ПРИЛОЖЕНИЕ 1)

2. Оглавление.

3. Постановку задачи.

4. Таблицу входных и выходных данных.

5. Метод решения задачи (если необходим).

6. Схему алгоритма.

7. Листинг (распечатку) текста программы.

8. Результаты решения в виде таблиц.

9. Анализ результатов и выводы.

10. Список литературы.

Настоящие методические указания предназначены для студентов всех специальностей и всех видов обучения, изучающих дисциплину «Информатика».

Тексты заданий частично заимствованы из методических указаний, разработанных на кафедре информатики СПб ЛТА [1, 2]. Задания 4.7 и 4.9 сформулированы доцентом СЛИ В. А. Деминым.

СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Анализ задачи

Прежде чем приступить к разработке программы, необходимо четко уяснить себе смысл поставленной задачи, изучить рекомендованную литературу и выработать подход к решению задачи. Результатом анализа является описание данных, основные математические формулы, связывающие исходные данные с результатами, краткое словесное описание алгоритма, а также вводимые ограничения.

Все данные можно поделить на три группы: входные (исходные данные), выходные (результаты) и промежуточные. Для исходных данных и результатов различают их внешнее представление, с которым будет работать пользователь программы, и внутреннее (имя в программе).

Пример описания данных:

Параметр (данное)	Обозначение	Размерность	Тип переменной	Формат	Имя в программе
Входные данные
Марка	M		строковая	\ \	MAR$
Количество	k	шт.	числ. целая	##	KOL%
Начальная скорость	Vн	м/с	числ. вещ.	##.##	VN
. . .	. . .	. . .	. . .	. . .	. . .
Промежуточные данные
. . .	. . .	. . .	. . .	. . .	. . .
Выходные данные
Время	t	с	числ. вещ.	##.#	T
Скорость	V	м/с	числ. вещ.	###.##	V
. . .	. . .	. . .	. . .	. . .	. . .

Выбор метода решения задачи

Для заданий, использующих численные методы (раздел 4), необходимо обосновать выбор конкретного метода для решения данной задачи, кратко изложить метод и привести расчетные формулы.

При затруднениях можно воспользоваться рекомендациями, пояснениями и расчетными формулами, приведенными в методических указаниях в конце каждого задания.

Разработка схемы алгоритма

Существуют различные способы записи алгоритмов. При работе над курсовым заданием рекомендуется использовать графический способ как один из наиболее наглядных и употребляемых.

При разработке алгоритма рекомендуется придерживаться модульного подхода. Принцип модульности состоит в том, что вся задача разбивается на несколько частей (подзадач) таким образом, чтобы каждая часть представляла собой небольшую самостоятельную задачу. Каждая такая часть оформляется в виде отдельной подпрограммы и называется модулем. Каждый модуль может быть разработан и отлажен отдельно от других, а затем уже отлаженные модули собираются в единую программу. В этом случае программа состоит из основной программы и набора подпрограмм.

Основная программа, содержащая вызовы подпрограмм, становится более понятной и обозримой, представляя собой описание общего плана выполнения алгоритма и перенося детальное описание отдельных его этапов в подпрограммы.

Схема алгоритма для каждого программного модуля изображается в виде отдельного рисунка. Сначала изображается схема алгоритма основной программы, а затем схемы отдельных подпрограмм.

Составление программы

Этот этап считается более простым в сравнении с предыдущими, однако для начинающего программиста и здесь могут встретится определенные сложности, так как для одного и того же алгоритма можно разработать программы, различающиеся по качеству.

Ниже приводятся некоторые советы, позволяющие улучшить качество программ.

· Если значение некоторого выражения используется в программе несколько раз, целесообразно ввести вспомогательную переменную для хранения этого выражения.

· Выражения, значения которых не изменяются при выполнении тела цикла, следует вычислять до входа в цикл, записывая значение во вспомогательную переменную.

· Избегайте оператора GOTO. Его можно во многих случаях исключить, применяя конструкцию IF-THEN-ELSE. При этом получаются более наглядные и понятные программы.

· Рекомендуется с помощью сдвига начала строк программы выделять ее управляющие структуры: метки, циклы, ветвления.

· Внимательно подходите к выбору имен переменных программы, старайтесь вместо безликих однобуквенных имен использовать содержательно - осмысленные. Помните, что «р» и «Р» или «n» и «N» - это одно и то же имя.

· Если в расчетах используется число p, то в начале программы необходимо записать оператор PI = 3,141593.

· Объявление размера массивов (DIM) выполняется один раз в самом начале программы.

· Не пренебрегайте комментариями в программе. Комментарии должны кратко и точно пояснять смысл основных шагов алгоритма, но не загромождать программу.

Оформление пояснительной записки

Весь отчет оформляется с помощью текстовых и графических редакторов Word, Paint и др. Печать односторонняя на стандартных листах (210´297).

Тексты должны быть набраны с переносом слов и выравниванием по ширине, межстрочный интервал одинарный, размер шрифта 12 или 14.

Формулы должны располагаться в отдельной строке с выравниванием по центру и должны быть набраны с помощью редактора формул Equation (меню Вставка/Объект/Microsoft Equation).

Таблицы создаются и редактируются с помощью меню Таблица и оформляются с помощью инструмента Обрамление.

Схема алгоритма целиком или отдельными модулями набирается графическим редактором Paint или инструментом Рисунок текстового редактора Word, или другими графическими редакторами.

Листинг программы и результаты вычислений в виде таблиц печатаются на стандартных листах и вшиваются в пояснительную записку.

Все разделы отчета снабжаются заголовками и нумеруются по порядку.

Все листы отчета (пояснительной записки) должны быть сброшюрованы, пронумерованы и помещены в специальную папку для курсовых работ.

Заключение и выводы.Этот раздел является обязательным. Обсуждается программа, указываются ее достоинства и слабые места, рассматриваются пути улучшения программы. Анализируются полученные результаты. Указываются недостатки постановки задачи, рекомендуются другие методы ее решения и т. д.

Оглавление.Располагается после титульного листа. Здесь дается перечень заголовков разделов, включая заключение и список литературы, с указанием номеров страниц отчета.

Список литературы. Располагается на последней странице отчета после заключения. Здесь перечисляются используемые в работе учебники, методические указания и другая литература. В тексте отчета даются ссылки на используемую литературу, указывается номер, присвоенный в списке, в квадратных скобках, например, [3] или [15].

Исходные данные

P, кВт	V	T, с/м3	L, м
100 (50) 200	0,6 (0,4) 1,4	20 (50) 120	150 (350) 850

Заданы начальное значение, шаг изменения (в скобках) и конечное значение каждого из исходных данных.

Исходные данные

Длина транспортера L, м	Длина бревна lср, м	Вес бревна Q, Н	Скорость V, м/с
90 (10) 120	3 (1) 6	600 (100) 900	0,6 (0,2) 1,2

Заданы начальное значение, шаг изменения (в скобках) и конечное значение каждого из исходных данных.

Исходные данные

Средняя длина хлыста l, м	Объем хлыста q, м3	Скорость подачи V, м/с
lmin	lmax	Dl	qmin	qmax	Dq	Vmin	Vmax	DV
			0,2	1,4	0,2	0.6	1.2	0.2

Исходные данные

Число хлыстов, Х	Расстояние трелевки l, м	Объем хлыста q, м3
Xmin	Xmax	DX	lmin	lmax	Dl	qmin	qmax	Dq
						0,2	0,6	0,1

Исходные данные

Расстояние трелевки, L; м	Расстояние подтрелевки l, м	Объем пачки Q, м3
Lmin	Lmax	DL	lmin	lmax	Dl	Qmin	Qmax	DQ
								0,5

Исходные данные

Давление Р, мПа	Угловая скорость w, об/мин	Объем насоса
Pmin	Pmax	DP	wmin	wmax	Dw	V(I), cм3
						32, 46, 58, 60

Исходные данные

Сила тяги, кН	m1, кН/т	m2, кН/т
Fmin	Fmax	DF	m1min	m1 max	Dm1	m2 min	m2 max	Dm2
			1,1	2,3	0,4	6,3	7,8	0,5

m₁ и m₂ - зависимые переменные (меняются одновременно).

Исходные данные

Коэффициент k	Запас леса q, м3/га	Трудоемкость U, чел.-дн./км
kmin	kmax	Dk	qmin	qmax	Dq	Umin	Umax	DU
0,1	0,5	0,2

Исходные данные

bm, м	hm, м	bp1,м	bp2, м	lx ,м	E, м3
				lx min	lx max	Dlx	Emin	Emax	DE
							105	8 · 105	105

Исходные данные

Толщина бруса d,м	Высота бруса h, м	Начальная температура
dmin	dmax	Dd	hmin	hmax	Dh	tо, oС
0,1	0,2	0,05	0,3	0,4	0,02	0; 15; 25

Исходные данные

Температура среды, °С	Время нагрева, час	Диаметр чурака, м
tc	tн	tк	Dt	Dн	Dк	DD
70; 78; 83; 90; 100			0,5	0,1	0,4	0,1

Светотехнический расчет

Определить ширину (размеры) окон промышленных зданий для указанных районов строительства.

Теоретическое значение ширины окна B, м, определяется по формуле

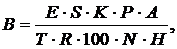
где S - площадь помещения, м ;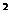

H - высота окна, м;

E - нормативное значение коэффициента естественного освещения (КЕО);

K - коэффициент запаса;

P - световая характеристика окна;

A - коэффициент, учитывающий затемнение окон противостоящими зданиями;

T - коэффициент светопропускания окна;

R - коэффициент, учитывающий повышение КЕО благодаря свету, отраженному от поверхностей помещения;

N - количество окон (может изменятся от 1 до 15).

По данным расчета Bвыбрать стандартную ширину окна В_СТ, м

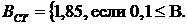
Результаты расчетов для всех районов строительства выдать в виде таблицы, содержащей графы N, B и B_СТ.

Исходные данные

Район строительства	E	S, м2	K	P	A	T	R	H, м
Лодейное поле	1,1		1,3	7,3		0,56	1,32	3,0
Подпорожье	1,05		1,25	7,1		0,6	1,35	3,2
Приозерск	1,15		1,28	6,9		0,58	1,3	3,25

Для каждого района строительства расчеты производить при N_нач.= 2, N_кон. = 8, DN = 1.

Теплотехнический расчет

Определить толщину наружных стен отапливаемых промышленных зданий из различных стеновых материалов для указанных районов строительства. Толщина стен должна обеспечивать необходимый для данного производства температурно-влажностный режим в помещении.

Теоретическое значение толщины стены (Д) определяется по формуле:

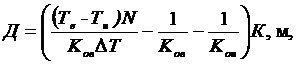
где Т_в - температура внутреннего воздуха, зависящая от назначения помещения, К;

Т_н - среднее значение температуры наружного воздуха, К;

N - коэффициент, зависящий от положения наружного ограждения по отношению к наружному воздуху;

К_он - коэффициент теплоотдачи наружной поверхности ограждения, Вт/м² × град;

К_ов - коэффициент теплоотдачи внутренней поверхности ограждения, Вт/м² × град;

DТ - нормируемый температурный перепад между температурой воздуха внутри помещения и температурой внутренней поверхности ограждения, К;

К - коэффициент теплопроводности материала стен, Вт/м × град.

По данным расчета Д выбрать стандартное значение Д_ст.

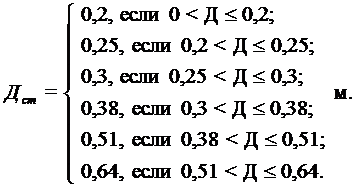
Результаты расчетов выдать в виде таблицы, содержащей графы: коэффициент теплопроводности материала K; толщина стен расчетная Д; толщина стен, выбранная Д_стдля всех районов строительства.

Исходные данные

Район строительства	ТН	ТВ	N	KОН	KОВ	DT
Лодейное поле				23,3	8,72
Подпорожье			1,01		8,8	7,9
Приозерск			0,95	23,5	8,75	8,1

Для каждого района строительства расчеты производить при K_i = 0,76; 0,7; 0,58; 0,44; 0,41; 0,17.

Исходные данные

Номер точки	Возраст xi, лет	Рост yi, м
		72,2 86,3 100,9 117,5 134,8 152,4 171,2

Исходные данные

Количество деталей	Количество отверстий на детали	Координаты центров отверстий на детали	Координаты расположения деталей на плате
Кд	М0	x, мм	y, мм	а, мм	b, мм	a, рад
						p/2
						p/4

Исходные данные

Номер отверстия
ri, мм
ai, рад		0,265	0,735		0,971	0,625	0,341	p/2

Исходные данные

dз, мм	dД, мм	ar	n, об/мин
		1; 1,5; 2	700, 750, 800

Исходные данные

Уклон волока a, рад	mт, кН/т	mг, кН/т	Масса тракт.	Сила тяги	Объем пачки
amin	amax	Da	m т min	mт max	Dmт	mг min	mг max	Dmг	G, т	FK, кН	V,м3
-0,3	0,3	0,1	1,1	2,3	0,4	6,3	7,8	0,5		97,2	0,2; 0,3

m_т и m_г - зависимые переменные (меняются одновременно).

Исходные данные

Порода древесины	Число режущих кромок, z	D, мм	n, об/мин	V, м/мин
сосна береза дуб	??? ???			0,5 0,8 1,0

Древесины

Произвести расчет силы и мощности резания при обработке партии деталей при чистовом осевом точении древесины. Основные зависимости величин, определяющих режимы резания:

Средняя скорость резанья V:

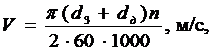
где d_З - диаметр заготовки, мм;

d_д - диаметр детали, мм;

n - скорость вращения древесины, об/мин;

Подача (D):

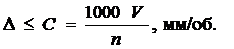
Рекомендуется D £ 0,8 для получения чистой поверхности.

Припуск h, мм; h = 1 мм.

Толщина стружки е, мм.

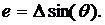
Длина лезвия (b):

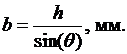
Среднее условное давление на поперечное сечение стружки К, кГ/мм²

для сосны:

К = (0,003 + 0,006q)d + (0,006 + 0,00016q)V - (0,06 + 0,023q),

для березы и дуба;

К = (0,005 + 0,0095q) d + (0,007 + 0,00022q)V - (0,09 + 0,023q).

Удельная сила (p), кГ/мм:

для сосны: р = 0,1 + 0,0042q,

для березы: р = 0,12 + 0,0048q,

для дуба: р = 0,15 + 0,006q.

Сила резания (Р):

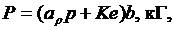
где а_r - коэффициент затупления резца,

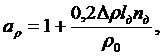
где а_r ³ 1;

r₀- начальный радиус кривизны лезвия, мкм;

l_{д -} длина реза на одну деталь, м;

n_д - количество деталей в партии;

Dr - прирост радиуса кривизны лезвия в результате затупления, мкм.

На один метр реза прирост радиуса кривизны лезвия резца Dr равен 0,001 мкм для резца из стали ХВТ и 0,008 мкм для резца из стали Х12Ф1.

Мощность резанья (N):

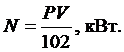
Найти зависимости силы и мощности резания после обработки партии деталей от независимых величин n и d.

Исходные данные

q, град.	d, град	n, об/ мин	rо	lд, м	nд	Марка стали.	dд, мм	dз, мм
	40; 45; 50	2500; 3000; 3500		1,0		ХВТ

Исходные данные

D, мм	h, мм	N зернистости	V, м/с
	0,5; 0,6; 0,7; 0,8		25, 30, 40, 50

ЗАДАНИЯ С ИСПОЛЬЗОВАНИЕМ ЧИСЛЕННЫХ МЕТОДОВ

Сформировать файлы исходных данных, предусмотреть возможность их обновления и вывода на бумагу. Произвести указанные в задании вычисления. Результаты оформить в виде таблицы. Сформировать файл результатов. По требованию из меню строить графики указанных в задании зависимостей.

Исходные данные

VН, м/с	VД, м/с	i	Q, т	PT, т
13,9; 11,1	8,33; 5,55; 0	-0,3; -0,2; 0; 0,2; 0,3		14,2

Для вычисления определенного интеграла рекомендуется воспользоваться формулой Симпсона

где n - число разбиений интервала [a, b];

H - шаг интегрирования, H = (b – a)/n;

x_i = a + iH;

i = 1, 2, ..., n-1.

Точность вычисления определенного интеграла e = 0,00001.

Исходные данные

В, м	Т, м	L, м	V, м/с
18, 27	1,8; 2; 2,5	120, 240	0,8; 1; 1,2

Значения коэффициента x, отличные от табличных значений, можно вычислить по формуле линейной интерполяции

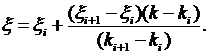
Исходные данные

Стоимость пилы С_п = 175 тыс. руб., стоимость лома C_л = 10 тыс. руб.

	t, час.	Y, тыс. руб. в зависимости от условий эксплуатации
		0,67	0,90	1,02	1,46	3,06
		1,77	1,96	2,29	2,66	6,01
		3,26	3,42	3,98	4,17	10,08
		5,18	5,80	6,21	6,60	16,10
		9,26	10,20	12,76	12,45	26,32
		18,84	21,48	21,64	24,66	48,40
		30,88	37,64	39,46	44,75	78,38
		46,09	52,68	63,46	84,51	116,82
		80,16	93,34	109,58	147,84	184,67

Для решения задачи квадратичной аппроксимации можно использовать следующие выражения:

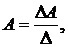
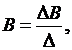
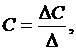
где определитель системы

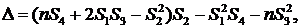
определители неизвестных:

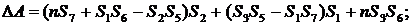
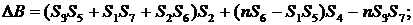
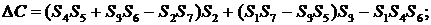
суммы:

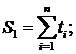
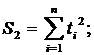
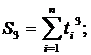
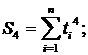
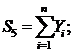
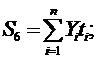
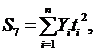
где n - количество точек, n = 9.

Определение диаметра трубы

Определить диаметр трубы, соединяющей озеро и колодец, если вода движется самотеком.

Диаметр трубы (d, м) определяется уравнением высокого порядка

Ad⁶ - Cd² - Bd - E=0, (4)

где

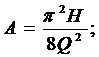
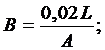
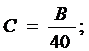
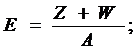
где H - напор воды;

Q - расход воды;

L - длина трубы;

Z и W - коэффициенты местных потерь.

Найти зависимость d от независимых переменных H, Q и L.

Исходные данные

Hmin	Hmax	DH	Qmin	Qmax	DQ	L	Z	W
			0,01	0,05	0,01	100; 150

Для уточнения корня уравнения высокого порядка можно использовать метод касательных (Ньютона):

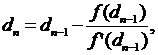
где n - номер итерации, n = 1, 2, 3, ...;

f(d_n-1) - значение функции, левой части уравнения (4), при очередном приближении;

f¢(d_n-1) - значение первой производной функции при очередном приближении.

Условие окончания вычислений

ïd_n – d_n-1ï £ e,

где e - точность вычислений, e = 10 ^-5.

Начать уточнение корня с d₀ = 0,2 м.

Исходные данные

Угол внутреннего трения	Плотность грунта дорожной одежды	Толщина дорожной одежды	Высота насыпи	Плотность грунта насыпи	Удельная сила сцепления с, Кн/м2
j, град	gДО, т/м3	hДО, м	hгр, м	gгр, т/м3	cн	cк	Dc
	1,8	0,3	1,5	1,4	0,02	0,2	0,02

Для уточнения корня трансцендентного уравнения вида a = j(a) удобнее использовать метод простых итераций:

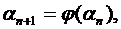
где n - номер итерации, n = 0, 1, 2, ...;

j(a_n) - значение правой части уравнения (5) при очередном приближении. Начать уточнение корня с a₀ = 0,7 рад.

Условие окончания вычислений:

ïa_n+1 – a_nï £ e,

где e - точность вычислений, e = 10^-4 рад.

Условие сходимости процесса j(a_n) > 1.

В случае непригодности метода простых итераций необходимо воспользоваться методом касательных или одним из других известных численных методов решения трансцендентных уравнений.

Исходные данные

d, м	x, м	t,час	tс, °С
0,6	-0,3; -0,2; -0,1; 0; 0,1 0,2; 0,3	2; 5; 10; 20	90; 80

Задание 4.9.

Необходимо решить задачи линейной и квадратичной аппроксимации для всех точек, т. е. найти коэффициенты a, b и c в функциях вида L = a + bt и L = a + bt + сt².

По результатам экспериментальных исследований на экране монитора построить точечную диаграмму. В том же масштабе другим цветом изобразить полученные прямую и параболу.

Произвести оценку полученных линейной и квадратичной зависимостей методом наименьших квадратов и сделать рекомендацию описания зависимости содержания лигнина в целлюлозе в процессе отбелки ее пароксидом водорода функциями вида L = a + bt или L = a + bt + сt². Смотри раздел 4.13.

Задание 4.10.

По результатам экспериментальных исследований на экране монитора построить точечную диаграмму.

Разбить всю зависимость на N зон (N £ 4), которые можно разделить вертикальными линиями. Решить задачу линейной аппроксимации для каждой зоны в отдельности, т. е. получить N уравнений вида L = a + bt. Смотри раздел 4.13.

На точечной диаграмме другим цветом в том же масштабе изобразить полученные прямые.

Задание 4.11.

По результатам экспериментальных исследований на экране монитора построить точечную диаграмму.

Разбить всю зависимость на N зон (N £ 4), которые можно разделить вертикальными линиями. Решить задачу квадратичной аппроксимации для каждой зоны в отдельности, т. е. получить N уравнений вида L = a + bt + сt². Смотри раздел 4.13.

На точечной диаграмме другим цветом в том же масштабе изобразить полученные кривые.

Задание 4.12.

По результатам экспериментальных исследований на экране монитора построить точечную диаграмму.

Разбить всю зависимость на N зон (N £ 4), которые разделить вертикальными линиями. Решить задачу линейной и квадратичной аппроксимации для каждой зоны в отдельности, т. е. получить по N уравнений вида L= a + bt и L = a + bt + сt².

Произвести оценку полученных линейной и квадратичной зависимостей для каждой зоны методом наименьших квадратов и сделать рекомендацию описания этой зоны функциями вида L = a + bt или L = a + bt + сt². Смотри раздел 4.13.

На точечной диаграмме другим цветом в том же масштабе изобразить рекомендованные зависимости для каждой зоны.

Приложение 1

Министерство общего и профессионального образования

Российской Федерации

Санкт-Петербургская государственная лесотехническая академия

Сыктывкарский лесной институт

Факультет__________________________

Курс_______________________________

Группа_____________________________

Специальность______________________

КУРСОВАЯ РАБОТА ПО ИНФОРМАТИКЕ

Тема ______________________________

Студент ___________________________

Руководитель ______________________

СЫКТЫВКАР 1999

Приложение 2

Фрагменты программ, наиболее часто используемых студентами при выполнении курсового задания (для алгоритмического языка QBasic).

Окна и меню

DIM B$ (13)

B$ (0)=" "

B$(1)= " КУРСОВАЯ РАБОТА ПО ИНФОРМАТИКЕ "

B$ (2)=" Выполнил Иванов Иван Иванович "

B$ (3)=" студент 2-го курса, специальность ТХПД, д/о "

B$ (4)=" 1998 г. "

B$ (5)=" "

B$ (6)=" СТАТИСТИКА ХИМИЧЕСКИХ РЕАКТОРОВ "

B$ (7)=" МЕНЮ: "

B$ (8)=" 1. Формирование файла данных "

B$ (9)=" 2. Просмотр файла данных "

B$ (10)=" 3. Загрузка файла данных и решение задачи "

B$ (11)=" 4. Графическая иллюстрация результатов "

B$ (12)=" 5. Выход "

B$ (13)=" "

COLOR 15,2:CLS ‘ цвет (цвет символов с 0 по15, цвет фона с 0 по 7)

LOCATE 4 ‘ установить курсор в 4-ой строке экрана

FOR I=0 TO 5

PRINT TAB(18): COLOR 15,1: PRINT B$(I): COLOR 15,2

NEXT I

LOCATE 23,22 ‘ установить курсор в 23-ой строке и 22-ой позиции экрана

COLOR 15 : PRINT "Для продолжения нажмите любую клавишу"

SLEEP 100 ' выждать 100 сек или нажать любую клавишу

7 COLOR 15,2 : CLS : LOCATE 6

FOR I=5 TO 13

PRINT TAB(18) :COLOR 14,6: PRINT B$(I):COLOR 15,2

NEXT I

LOCATE 17,25: COLOR 15,5

INPUT " ВВЕДИТЕ НУЖНЫЙ НОМЕР"; NM:COLOR 15,2

6 ON NM GOTO 1,2,3,4,5

LOCATE 20,27: COLOR 14 : INPUT "Уточните номер"; NM : GOTO 6

1 ‘ Формирование файла данных

COLOR 7,0 : CLS

. . . .

GOTO 7

2 ‘ Просмотр файла данных

COLOR 7,0 : CLS

. . . .

LOCATE 23,18

COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"

SLEEP 100 : GOTO 7

3 ‘ Загрузка файла данных и решение задачи

COLOR 7,0 : CLS

. . . .

LOCATE 23,18

COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"

SLEEP 100 : GOTO 7

4 ‘ Графическая иллюстрация результатов

COLOR 7,0 : CLS

. . . .

LOCATE 23,18

COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"

SLEEP 100 : GOTO 7

5 COLOR 7,0 : CLS

END

Вывод таблиц результатов

CLS

READ TN,TK,HT,A

DATA 0,20,2,3.2

Z$=" Равноускоренное движение точки "

L$="———————--———————————————————"

H$="| № п/п | t, сек | S, м | V, м/с |"

F$="| ## | ## | ###.# | ##.# |"

PRINT Z$

PRINT L$

PRINT H$

PRINT L$

N=1

FOR T=TN TO TK STEP HT

S=A*T^2/2

V=A*T

PRINT USING F$;N,T,S,V

N=N+1

NEXT T

PRINT L$

END

Формирование файла данных

' Формирование файла данных на дискете

OPEN "a:dan" FOR OUTPUT AS #1 ' открыть файл для записи

INPUT "Размер массива K=";K ' размер массивов

WRITE #1, K ' записать на дискету

DIM X(K),Y(K),P$(K)

FOR I=1 TO K

INPUT "X(I),Y(I),P$(I) " ; X(I),Y(I),P$(I) ‘ ввод элементов строки

WRITE #1,X(I),Y(I),P$(I) ‘ запись строки на дискету

NEXT I

INPUT L,F,D,R,A$ ‘ ввод простых переменных

WRITE #1,L, F,D,R,A$ ' запись простых переменных на дискету

CLOSE #1 ' закрыть файл

END

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Панфилов И. И. и др. Вычислительная техника и программирование: Методические указания. - Л.: ЛТА, 1989. - 44 с.

2. Панфилов И. И. и др. Применение ЭВМ в отрасли: Методические указания. - Л.: ЛТА, 1989. - 34 с.

3. Завьялов А. С. и др. Вычислительная техника и программирование: Методические указания по курсовому проектированию. - Вологда: ВПИ, 1991. - 45 с.

4. Мельникова О. И. и др. Программирование на языке Qbasic. - М: Издательство ЭКОМ, 1997. -303 с.

5. Демидович Б. П., Марон И. А. Основы вычислительной математики. - М.: Физматгиз, 1960. 659 с.

6. Виноградов Г. К. Технология лесозаготовок. - М.: Издательство «Лесная промышленность», 1986. - 255 с.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ..............................................................................................................

1.СОДЕРЖАНИЕ КУР