Задачи с булевыми переменными

Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные могут принимать только одно из двух значений: 0 или 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми. На рис.1.18 представлена экранная форма с решением некоторой двухиндексной задачи с булевыми переменными.

Рис.1.18. Решение двухиндексной задачи с булевыми переменными

Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:

· для наглядности восприятия ввести в экранную форму слово "булевы" в качестве характеристики переменных (см. рис.1.18);

· в окне "Поиск решения"добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис.1.19).

Рис.1.19. Добавление условия единичной верхней границы значений переменных двухиндексной задачи с булевыми переменными

Вид окна "Поиск решения"для задачи с булевыми переменными, представленной на рис.1.18, приведен на рис.1.20.

Рис.1.20. Окно "Поиск решения"для задачи с булевыми переменными, представленной на рис.1.18

ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ

1. Каковы основные этапы решения задач ЛП в MS Excel?

2. Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений?

3. В чем смысл использования символа $ в формулах MS Excel?

4. В чем различие использования в формулах MS Excel символов ; и :?

5. Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения?

6. Каким образом в MS Excel задается направление оптимизации ЦФ?

7. Какие ячейки экранной формы выполняют иллюстративную функцию, а какие необходимы для решения задачи?

8. Как наглядно отобразить в экранной форме ячейки, используемые в конкретной формуле, с целью проверки ее правильности?

9. Поясните общий порядок работы с окном "Поиск решения".

10. Каким образом можно изменять, добавлять, удалять ограничения в окне "Поиск решения"?

11. Какие сообщения выдаются в MS Excel в случаях: успешного решения задачи ЛП; несовместности системы ограничений задачи; неограниченности ЦФ?

12.Объясните смысл параметров, задаваемых в окне "Параметры поиска решения".

13. Каковы особенности решения в MS Excel целочисленных задач ЛП?

14. Каковы особенности решения в MS Excel двухиндексных задач ЛП?

15. Каковы особенности решения в MS Excel задач ЛП с булевыми переменными?

ВАРИАНТЫ

Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл.1.5).

Таблица 1.5

Варианты задач к лабораторной работе №1

№ варианта	Математическая модель

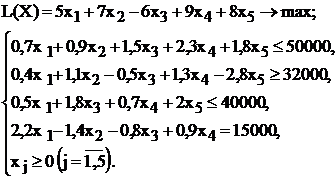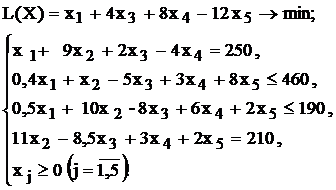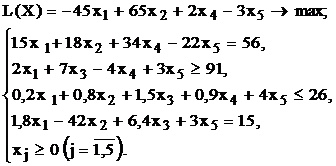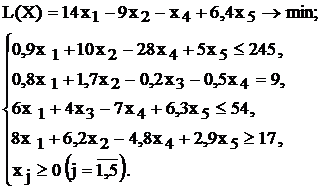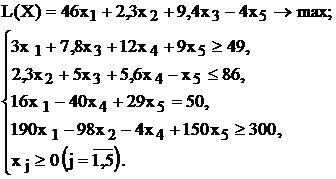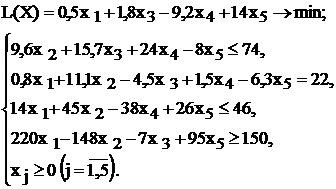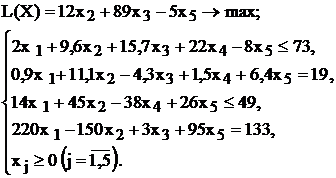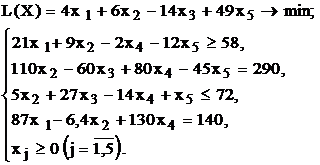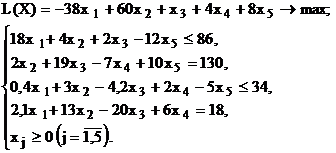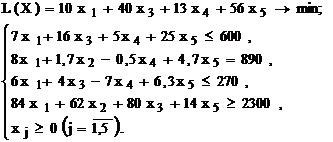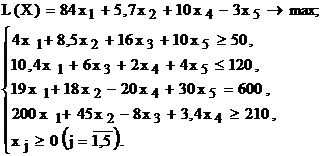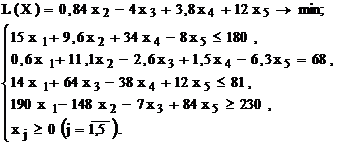БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: Учеб. пособие. – М.: Финансы и статистика, 2001. – 368 с.

2. Исследование операций в экономике: Учебн. пособие для вузов. / Под ред. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 407 с.

3. Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. – М.: Финансы и статистика, 2001. – 544 с.

4. Шапкин А. С., Мазаев Н. П. Математические методы и модели исследования операций: Учебник. –М.: «Дашков и К^о», 2004. – 400 с.

5. Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие. – М.: ЮНИТИ, 2001. - 368 с.

6. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов. / Под ред. В. В. Федосеева. – М.: ЮНИТИ, 1999.

7. Экономико-математические методы и модели: Учеб. пособие для студентов экономических специальностей вузов. /Под ред. А. В. Кузнецова (Н. И. Холод, А. В. Кузнецов, Я. Н. Жихар) – Мн.: БГЭУ, 2000. – 413 с.

Лицензия РБ на издательскую деятельность №0261 от 10 апреля 1998 года.

Подписано в печать ___________ 2006 г. Формат 60х84. Бумага типографская. Гарнитура Таймс. Усл. печ. л. _______. Усл. изд. л. _______. Тираж _______экз. Заказ № __________.

Издательство Башкирского государственного агарного университета.

Кафедра статистики и информационных систем в экономике