С двумя переменными
Графический метод решения ЗЛП удобно применять в том случае, если ограничения записаны в стандартной форме, а число переменных- две.
Графически решить задачу линейного программирования при следующих условиях:
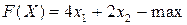
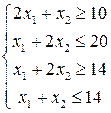
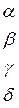

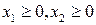 .
.
Областью решения линейного неравенства с двумя переменными является полуплоскость, лежащая по одну сторону граничной прямой. Уравнение этой прямой получается, если в соответствующем ограничении заменить знак неравенства знаком равно. Для данной системы неравенств получим уравнения четырёх граничных прямых.
Придавая поочерёдно переменным 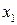 , а затем
, а затем 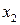 значение, равное нулю, находим координаты точек пересечения прямых с осями координат. Например, прямая
значение, равное нулю, находим координаты точек пересечения прямых с осями координат. Например, прямая 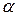 пересекает оси координат в точках (0;10) и (5;0). Прямая
пересекает оси координат в точках (0;10) и (5;0). Прямая 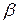 отсекает на оси
отсекает на оси 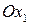 отрезок 20, а на оси
отрезок 20, а на оси 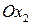 отрезок 10. Последовательно строим все границы области.
отрезок 10. Последовательно строим все границы области.
Для того, чтобы определить расположение соответствующей полуплоскости относительно граничной прямой, подставляем координаты любой точки, не лежащей на прямой (проще всего точку 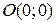 ) в левую часть соответствующего неравенства. Например, после подстановки в неравенство
) в левую часть соответствующего неравенства. Например, после подстановки в неравенство 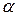 координат 0 и 0, получаем неверное неравенство
координат 0 и 0, получаем неверное неравенство 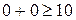 . Поэтому области решения неравенства
. Поэтому области решения неравенства 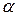 начало осей координат не принадлежит, а принадлежит полуплоскость, расположенная выше и левей прямой
начало осей координат не принадлежит, а принадлежит полуплоскость, расположенная выше и левей прямой 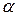 . А области решения неравенства
. А области решения неравенства 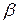 начало осей координат принадлежит. Значит, принадлежит области решения неравенства вся нижняя левая часть полуплоскости относительно прямой
начало осей координат принадлежит. Значит, принадлежит области решения неравенства вся нижняя левая часть полуплоскости относительно прямой 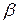 .
.
Многоугольником допустимых решений является общая часть всех выбранных полуплоскостей, т.е. четырёхугольник АВСD. Координаты вершин четырёхугольника, являющиеся опорными планами, найдем, решая совместно соответствующие пары линейных уравнений.
В вершине А пересекаются прямые 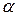 и
и 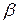 . Координаты вершины А найдём из решения системы уравнений:
. Координаты вершины А найдём из решения системы уравнений:
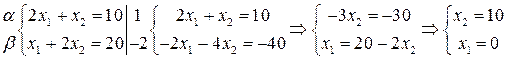 А(0;10).
А(0;10).
В вершине В пересекаются прямые 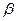 и
и 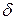 . Координаты В находим из решения системы уравнений:
. Координаты В находим из решения системы уравнений:
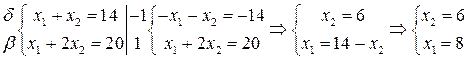 В(8;6).
В(8;6).
Аналогично находим координаты остальных вершин. Координаты вершины С:(14;0); вершины D:(2;6). Строим многоугольник решений. 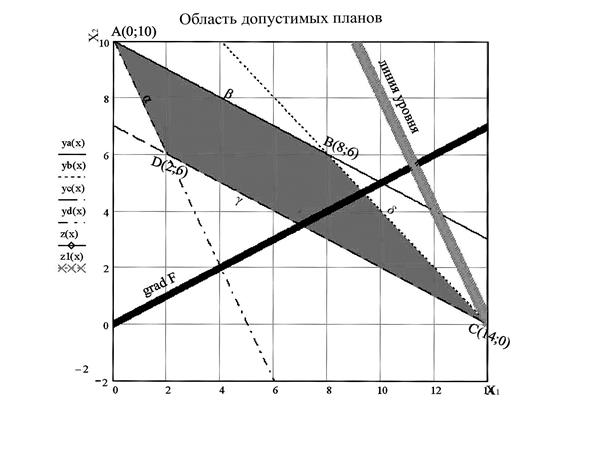
Из начала осей координат проведем вектор 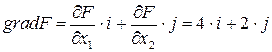 , координаты которого равны коэффициентам при соответствующих переменных в целевой функции. Вектор
, координаты которого равны коэффициентам при соответствующих переменных в целевой функции. Вектор 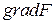 указывает направление наиболее быстрого возрастания целевой функции. На прямых, перпендикулярных вектору
указывает направление наиболее быстрого возрастания целевой функции. На прямых, перпендикулярных вектору 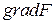 , целевая функция сохраняет постоянное значение. Эти прямые называются линиями уровня. В данной задаче одна из линий уровня совпадает с прямой AD
, целевая функция сохраняет постоянное значение. Эти прямые называются линиями уровня. В данной задаче одна из линий уровня совпадает с прямой AD 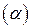 :
: 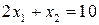 . В каждой точке этой прямой значение целевой функции постоянно и равно
. В каждой точке этой прямой значение целевой функции постоянно и равно 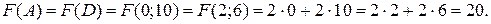 Это наименьшее значение целевой функции в области допустимых планов. Проекция точки С на вектор
Это наименьшее значение целевой функции в области допустимых планов. Проекция точки С на вектор 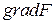 максимальна, поэтому в точке С целевая функция принимает максимальное значение:
максимальна, поэтому в точке С целевая функция принимает максимальное значение: 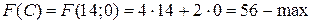 . Дополнительно определим значение целевой функции в вершине В.
. Дополнительно определим значение целевой функции в вершине В. 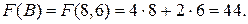 Это значение является промежуточным. Задача ЛП графическим методом решена.
Это значение является промежуточным. Задача ЛП графическим методом решена.
