Определение. Сочетаниями с повторениями из n по m называются неупорядоченные m-элементные выборки, в которых элементы могут повторяться.

Число сочетаний с повторениями из n по m обозначается 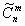В отличие от обычных сочетаний, где m 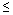n , в сочетаниях с повторениями m и n могут быть любыми. Формулу для вычисления числа сочетаний с повторениями выведем на основе следующего частного примера.

Пример 9.1. В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 5 открыток?

Решение. Ясно, что в купленном наборе открыток они будут повторяться и порядок их в наборе не важен, то есть это будут сочетания с повторениями из 3 по 5. Зашифруем все возможные наборы из 5 открыток следующим образом: открытки каждого вида изобразим в виде единиц, разделенных символами #. Так выборка 11#1#11 означает, что мы купили 2 открытки первого вида, одну - второго и 2 открытки третьего вида, а ##11111 - все 5 открыток третьего вида. Подсчитаем количество таких выборок. Каждая из них состоит из 7 элементов: пяти единиц и двух трегольников, то есть состав не меняется, а меняется только порядок элементов. Значит, это будут перестановки с повторениями из 7 элементов, где # повторяется два раза, а 1 - пять раз.

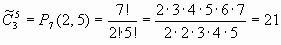
Ответ: 21способом

В общем случае, если имеется n видов открыток, а купить надо m штук, получим:

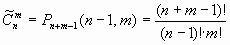(1.10)

Это и есть формула числа сочетаний с повторениями, однако она неудобна для запоминания, поэтому представим эту формулу в другом виде. Для этого вычислим 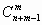по

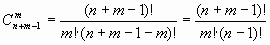
и сравним с (1.10). Правые части этих равенств равны. Приравнивая левые части, получим формулу, выражающую число сочетаний с повторениями через обычное число сочетаний.

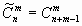(1.11)

Пример 9.2. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба?

Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ, ...

Состав меняется от выборки к выборке, значит, это уже не перестановки; порядок элементов несущественен, это - сочетания с повторениями из 2 по 6.

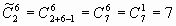
Cделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7.

Ответ: 7 вариантов

Пример 9.3. Сколько существует прямоугольных параллелепипедов, длина ребра которых выражается целым числом от 1 до 9?

Решение.Параллелепипед определяется тремя ребрами, поэтому его можно представить в виде тройки чисел. Выпишем несколько вариантов: (1,1,5); (2,7,9); (4,4,4) ... Элементы в выборке могут повторяться, состав меняется, порядок не существенен, например, выборки (2,7,9) и (9,2,7) соответствуют одному и тому же параллепипеду. Применяем формулу сочетаний с повторениями

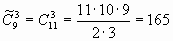
Ответ: 165 параллелепипедов

10. Схема определения вида комбинации

Приведем в систему полученные формулы всех 6 видов комбинаций с повторениями и без повторений, представив алгоритм определения вида комбинации следующей схемой.

Решим несколько задач с применением данной схемы.

Пример 10.1. В магазине игрушек имеются 7 одинаковых Чебурашек и 2 одинаковых Крокодила. Сколькими способами их можно расставить в один ряд на витрине?

Решение.Обозначив игрушки первыми бувами названия, составим несколько комбинаций: КЧЧЧЧЧЧЧК, ЧЧЧКЧКЧЧЧ, ККЧЧЧЧЧЧЧ, ... Повторяются ли элементы в выборке? Да. Меняется ли состав? Нет, ведь каждая выборка состоит из семи букв "Ч" и двух букв "К". Следовательно, это перестановки с повторениями.

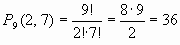
Ответ: 36 способами.

Пример 10.2. На окружности расположено 20 точек. Сколько существует вписанных треугольников с вершинами в этих точках?

Решение. Занумеруем точки числами от 1 до 20. Тогда каждый вписанный треугольник будет представлять собой тройку чисел. Выпишем несколько выборок: (1, 5, 19), (15, 2, 9), (14, 13, 7) .... Числа в выборке не могут повторяться, так как все вершины треугольника различны. Состав меняется от выборки к выборке, порядок не существенен, так как (1, 5, 19) и (19, 5, 1) - один и тот же треугольник. По схеме получается, что это сочетания без повторений из 20 по 3.

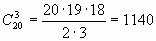
Ответ:1140 треугольников.

Пример 10.3. В некотором сказочном государстве не было двух жителей с одинаковым набором зубов (либо у них разное число зубов, либо зубов нет в разных местах). Оцените наибольшую численность населения этого государства, если максимальное число зубов у человека - 32.

Решение. Закодируем каждого жителя набором из 32 нулей и единиц. Единица соответствует наличию зуба в данном месте, нуль - его отсутствию. Выпишем несколько комбинаций: 11111...11, 1010...11, 00000...00, ...Элементы повторяются, состав меняется, порядок существенен. Это - размещения с повторениями из 2 по 32.

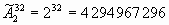
Ответ: 429 4967 296 жителей

Пример 10.4. Имеются в неограниченном количестве палочки длиной 5, 6, 7, 8, 9, 10 сантиметров. Сколько различных треугольников можно из них составить?

Решение. Составим несколько выборок: (5,5,5); (6,7,8); (8,9,9).. Элементы повторяются, состав меняется, порядок не существенен. Согласно схеме, применяем формулу сочетаний с повторениями из 6 по 3:

.

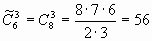Однако, здесь есть небольшой подвох: треугольника со сторонами 5, 5, 10 не существует, так что их будет 55.

Ответ: 55 треугольников