Практической работы №8 по теме
«Прямая и плоскость в пространстве»
Задача №1.Из точки M проведена к плоскости α наклонная MF длинной 14 см. Угол между наклонной и плоскостью равен 60°, найти расстояние от точки M до плоскости α.

Дано: М∉α, MF- наклонная, MF = 14 см;
MN⊥α, FN- проекция наклонной;
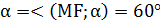 ,
,
Найти: 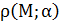
Решение:
1) По определенным перпендикулярности прямой и плоскости: 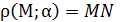
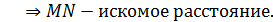
2) По определению перпендикулярности прямой и плоскости: 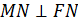 ,
,
так как 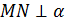 и
и 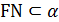 . Значит, треугольник MNF - прямоугольный.
. Значит, треугольник MNF - прямоугольный.
3) Решим прямоугольный 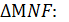
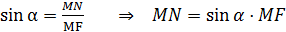 ,
,
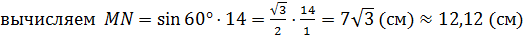 .
.
Ответ: 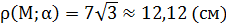 .
.
Задача №2. Из вершины А прямоугольника ABCD восстановлен перпендикуляр AN к плоскости прямоугольника. Найти расстояние от точки N до плоскости прямоугольника, если известны расстояния от этой точки до трёх вершин прямоугольника: 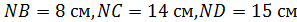 .
.
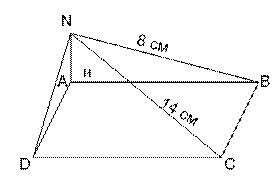

Дано: ABCD- прямоугольник,
AN- перпендикуляр к плоскости (ABC),
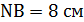 ,
, 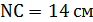 ,
, 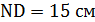
Найти: 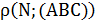
Решение:
1) По определению расстояния от точки до плоскости: 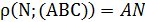 , тогда
, тогда
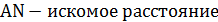 .
.
2) По теореме о трёх перпендикулярах: 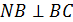 , так как
, так как
NB- наклонная к плоскости (ABC), AB- её проекция на плоскость (ABC),
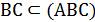 и
и 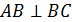 (так как ABCD- прямоугольник).
(так как ABCD- прямоугольник).
3) По теореме Пифагора в треугольнике NBC:
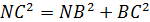 , тогда
, тогда 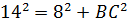 , отсюда находим
, отсюда находим
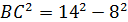 ,
, 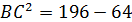 ,
, 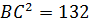 ,
, 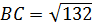 .
.
4) По определению перпендикулярности прямой и плоскости:
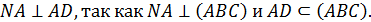 Значит, треугольник
Значит, треугольник
NAD -прямоугольный, по теореме Пифагора: 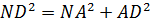 ,
,
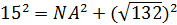 ,
, 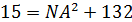 ,
, 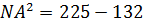 ,
, 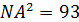 ,
,
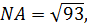
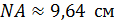 .
.
Ответ: 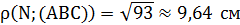 .
.
Методические указания и примеры типового расчёта
Практической работы №9 по теме
«Дифференцирование функций»
Теория
Формулы дифференцирования:
1) производная постоянной: 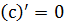
2) производная аргумента: 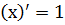
3) производная суммы функций: 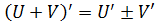
4) производная произведения двух функций: 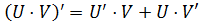
5) производная частного двух функций: 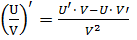
Определение: Сложной функцией называется функция, аргументом которой является другая функция.
Сложная функция  это функция от функции.
это функция от функции.
Правило дифференцирования сложной функции: разбить функцию на простые функции, найти производные от всех простых функций и эти производные перемножить.
Пример 1.Найти производную функции 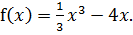
Решение:
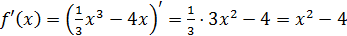 .
.
Пример 2.Найти производную функции 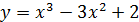
Решение:
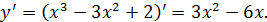
Пример 3.Найти производную функции 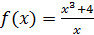 .
.
Решение:
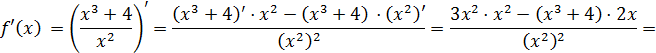
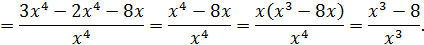
Методические указания и примеры типового расчёта
Практической работы №10 по теме
«Неопределенный и определенный интегралы»
Теория
Определение. Первообразной функцией для функции 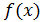 называется такая функция
называется такая функция 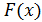 , производная от которой равна
, производная от которой равна 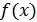 : F'(x) = f(x).
: F'(x) = f(x).
Определение. Неопределённый интеграл 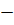 это совокупность всех первообразных функций
это совокупность всех первообразных функций 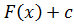 для дифференциала
для дифференциала 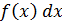 :
:
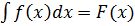 +c
+c
Основныесвойства неопределенного интеграла:
1.Дифференциал неопределённого интеграла равен подынтегральному выражению: d 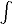 f(x)dx = f(x)dx.
f(x)dx = f(x)dx.
2. Неопределённый интеграл от дифференциала функции равен самой этой функции, сложенной с произвольной постоянной: 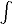 dF(x) = F(x)+C.
dF(x) = F(x)+C.
3. Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме неопределённых интегралов от каждой функции:
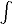 (
( 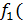 x)+
x)+ 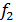 (x))dx =
(x))dx = 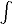
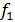 (x)dx+
(x)dx+ 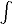
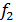 (x)dx.
(x)dx.
4.Постоянный множитель можно вынести за знак неопределённого интеграла (как множитель): 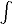 kf(x)dx = k
kf(x)dx = k 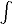 f(x)dx, где k-постоянный множитель.
f(x)dx, где k-постоянный множитель.
Таблица основных формул интегрирования
1. 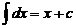 ; 2.
; 2. 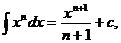

 n
n 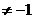 9.
9. 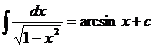
3. 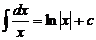 , 4.
, 4. 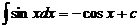 , 10.
, 10. 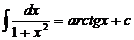
5. 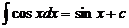 , 6.
, 6. 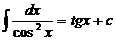 ,
,
7. 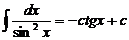 , 8.
, 8. 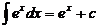 ,
,
Метод непосредственного интегрирования
Непосредственным интегрированием называется такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
