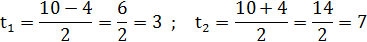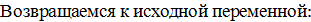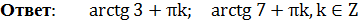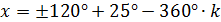Практической работы №6 по теме

«Решение тригонометрических уравнений и неравенств»

Теория

Простейшими тригонометрическими уравнениями называются уравнения вида

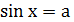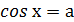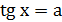, , или .

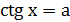При 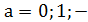1 для решения уравнений удобно пользоваться тригонометрическим кругом.

В остальных случаях будем применять общую формулу корней тригонометрического уравнения, которая приведена в таблице решений простейших тригонометрических уравнений.

Таблица решений простейших тригонометрических уравнений

Уравнение вида	Общая формула корней уравнения	Промежуток главного угла
	,

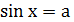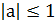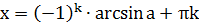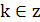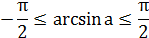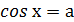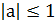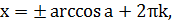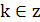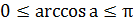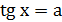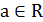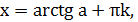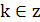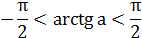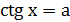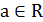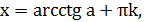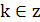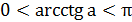Примеры типовых расчётов

1) Решить уравнение: .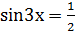

Решение:

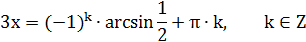
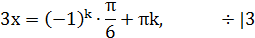
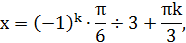
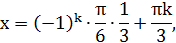
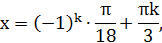
Ответ: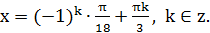

Найти 3 корня этого уравнения:

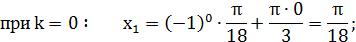
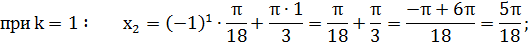
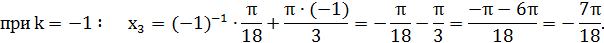
Ответ: .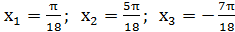

Вывод: убедились, что в общей формуле корней тригонометрического уравнения содержится бесчисленное множество решений.

2) Решит уравнение: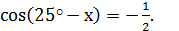

Решение:

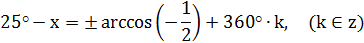
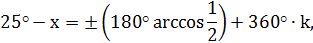
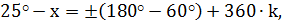
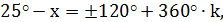
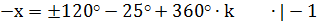
- эту общую формулу корней можно разбить на две группы:

;

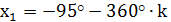- I группа и 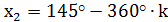-II группа

Ответ: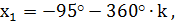

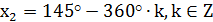
Назвать 5 корней уравнения:

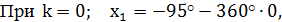
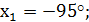
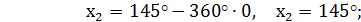
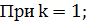
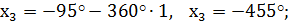
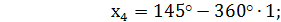
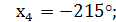
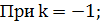
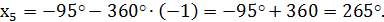
Ответ: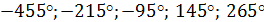

3) Решит уравнение:

.

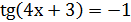Решение:

.

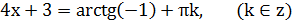
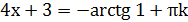
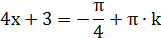
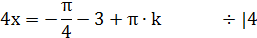
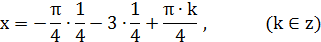
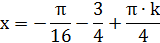
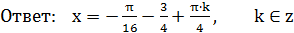Указать два корня уравнения:

,

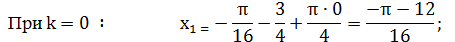
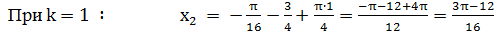Ответ: .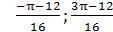

4) Решить уравнение: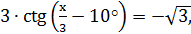

Решение:

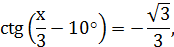
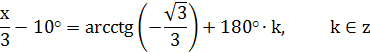
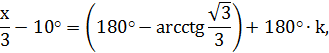
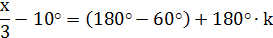
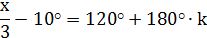
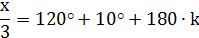
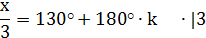
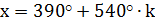
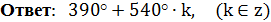
Метод подстановни при решении тригонометрических

Уравнений (приведение уравнения к квадратному)

В некоторых случаях удается сделать замену переменной:

Cos x=t или sin x=t, или tg x=t, или ctg x =t.

Тогда получается, как правило квадратное уравнение. Решим его и возвращаемся к исходной переменной. И в результате получаем простейшее тригонометрическое уровнение:

Помни: sin²x+cos²x=1

sin²x=1-cos²x cos²x=1-sin²x

1) Решить уравнение: .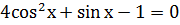

Решение:

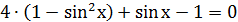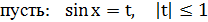, , тогда получим

,

,

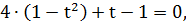
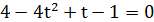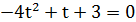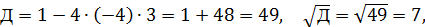
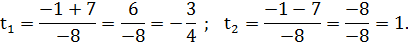
Возвращаемся к исходной переменной:

sin x =1 или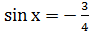

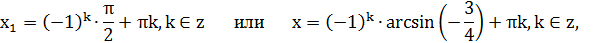
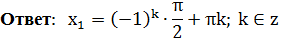
2) Решить уравнение: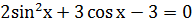

Решение:

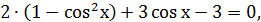
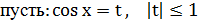, тогда получим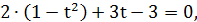

,

.

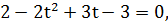
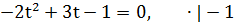
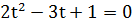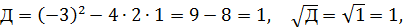
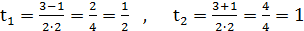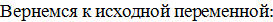
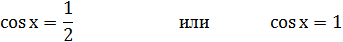
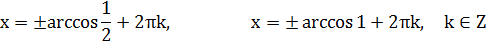
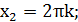
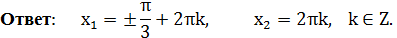
Однородные тригонометрические уравнения

Определение: Однородным тригонометрическим уровнением называется уравнение, в котором каждое слагаемое имеет одинаковую степень относительно функций sin𝛼 и cos𝛼.

Метод решения однородного тригонометрического уровнения:

Разделить обе части уравнения на cosⁿ x или sinⁿx, где n-степень (порядок) этого уравнения.

Тогда это уравнение сведется к уравнению относительно tg x или ctg x, и можно применить метод замены переменной.

1) Решить уравнение: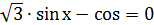

Решение:

Это однородное тригонометрическое уравнение I степени, разделим обе части уравнения на :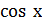

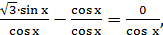отсюда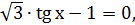

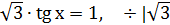
получили простейшее тригонометрическое уравнение

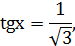
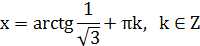
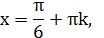
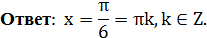
2) Решить уравнение: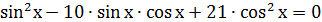

Решение:

Однородное тригонометрическое уравнение II степени, разделить обе части уравнения на cos²x:

,

,
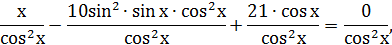
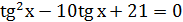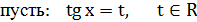
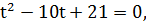
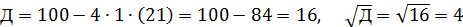