Дисперсия генеральной совокупности неизвестна.

Если дисперсия генеральной совокупности неизвестна (например, в случае малых выборок), то в качестве критерия проверки нулевой гипотезы принимают случайную величину 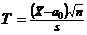, где s — исправленное среднее квадратическое отклонение. Величина Т имеет распределение Стьюдента c 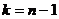степенями свободы.

Критическая область строится в зависимости от вида конкурирующей гипотезы. Поскольку это делается так, как описано выше, ограничимся правилами проверки нулевой гипотезы.

Правило 1.Для того чтобы, при заданном уровне значимости 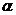, проверить нулевую гипотезу о равенстве неизвестной генеральной средней а (нормальной совокупности с неизвестной дисперсией) гипотетическому значению а₀, при конкурирующей гипотезе , надо:

1) вычислить наблюдаемое значение критерия: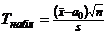

2)по таблице критических точек распределения Стьюдента (приложение 6), по заданному уровню значимости 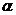, помещенному в верхней строке таблицы, и числу степеней свободы 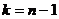, найти критическую точку .

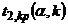3) Если 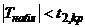— нет оснований отвергнуть нулевую гипотезу.

Если 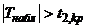— нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезе , по уровню значимости 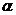, помещенному в нижней строке таблицы (приложение 6), и числу степеней свободы 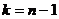, находят критическую точку 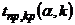правосторонней критической области.

Если 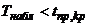— нет оснований отвергнуть нулевую гипотезу.

Если 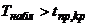— нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезе сначала находят «вспомогательную» критическую точку 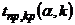и полагают границу левосторонней критической области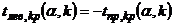

Если 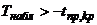— нет оснований отвергнуть нулевую гипотезу.

Если 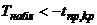— нулевую гипотезу отвергают.

Пример 3.1 (продолжение). Случай 1.

Вывод.

Случай 2.

Вывод.

Случай 3.

Вывод.

Замечание 1.Можно показать, что отыскивая двустороннюю критическую область при уровне значимости а, тем самым находят и соответствующий доверительный интервал с надежностью 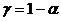. В случае 3.4.1 это доверительный интервал при известном СКО, с случае 3.4.2 – при неизвестном СКО.

Замечание 2. Отыскание двусторонней критической области и доверительного интервала приводит к одинаковым результатам, но истолкование этих результатов различно. Двусторонняя критическая область определяет границы (критические точки), между которыми заключено 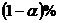числа наблюдаемых критериев, найденных при повторении опытов. Доверительный интервал определяет границы (концы интервала), между которыми в 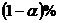опытов заключено истинное значение параметра.

Замечание 3. Если заранее задана точность 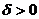, величину которой не должна превышать абсолютная величина расхождений между выборочной и гипотетической генеральной средними (при известном генеральном СКО 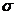), то минимальный объём выборки, обеспечивающий эту точность, можно найти по формул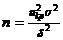е: , где 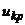определяется по равенству 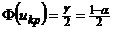. Если же 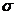неизвестно, но найдена его оценка 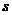, то 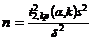.