Дисперсия генеральной совокупности известна

Пусть генеральная совокупность X распределена нормально, причем генеральная средняя а, хотя и неизвестна, но имеются основания предполагать, что она равна гипотетическому (предполагаемому) значению а₀.

Пример.Пусть X — совокупность размеров х, партии деталей, изготовляемых станком-автоматом, то можно предположить, что генеральная средняя а этих размеров равна проектному размеру а₀. Чтобы проверить это предположение, находят выборочную среднюю 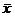и устанавливают значимо, или незначимо, различаются 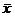и а₀. Если различие окажется незначимым, то станок обеспечивает в среднем проектный размер; если различие значимое, то станок требует подналадки.

Предположим, что дисперсия генеральной совокупности известна, например, из предшествующего опыта, или найдена теоретически, или вычислена по выборке большого объема (по большой выборке можно получить достаточно хорошую оценку дисперсии).

Пусть из нормальной генеральной совокупности извлечена выборка объема п и по ней найдена выборочная средняя 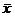,причем генеральная дисперсия известна. Требуется по выборочной средней, при заданном уровне значимости, проверить нулевую гипотезу о равенстве генеральной средней а гипотетическому значению а₀.

Учитывая, что выборочная средняя является несмещенной оценкой генеральной средней, т.е. , нулевую гипотезу можно записать так: . Таким образом, требуется проверить, что математическое ожидание выборочной средней равно гипотетической генеральной средней. Другими словами, надо установить значимо, или незначимо, различаются выборочная и генеральная средние.

В качестве критерия проверки нулевой гипотезы примем случайную величину , которая распределена нормально, причем, при справедливости нулевой гипотезы, , .

Критическая область строится в зависимости от вида конкурирующей гипотезы так же, как в предыдущем пункте. Обозначим значение критерия U, вычисленное по данным наблюдений через U_набл.

Правило 1.Для того чтобы, при заданном уровне значимости проверить нулевую гипотезу о равенстве генеральной средней а нормальной совокупности с известной дисперсией гипотетическому значению а₀, при конкурирующей гипотезе , надо:

1) вычислить наблюдаемое значение критерия

2)по таблице функции Лапласа (приложение 1, тетрадь 2) найти критическую точку двусторонней критической области по равенству .

3) Если — нет оснований отвергнуть нулевую гипотезу.

Если — нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе , критическую точку правосторонней критической области находят по равенству .

Если — нет оснований отвергнуть нулевую гипотезу.

Если — нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезе сначала находят критическую точку и_кр по правилу 2, а затем полагают границу левосторонней критической области

Если — нет оснований отвергнуть нулевую гипотезу.

Если — нулевую гипотезу отвергают.

Пример 3.1 (продолжение). Случай 1.

Вывод.

Случай 2.

Вывод.

Случай 3.

Вывод.