Принцип практической невозможности маловероятных событий

При решении практических задач приходится иметь дело с событиями, вероятность которых близка к нулю. Такие события называют маловероятными. В общем случае нельзя считать, что при единичном испытании маловероятное событие не произойдёт совсем. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает. На основании этого факта принимают следующий

Принцип практической невозможности маловероятных событий: если случайное событие имеет очень малую вероятность, то можно считать, что в единичном испытании это событие не наступит.

Замечание. На вопрос, насколько малой должна быть вероятность события, чтобы можно было считать его появление невозможным в одном испытании, однозначно ответить нельзя. Для задач, различных по существу, ответы будут разными.

Определение 7.Достаточно малую вероятность, при которой (в данной определённой задаче) событие можно считать практически невозможным, называют уровнем значимости.

Замечание 1. На практике обычно применяют уровни значимости, заключённые между числами 0,01 и 0,05. Уровень значимости 0,01 называют однопроцентным.

Замечание 2. Принцип практической невозможности маловероятных событий позволяет делать предсказания о событиях, вероятность которых близка к единице. Действительно, если событие А имеет вероятность, близкую к нулю, то противоположное ему событие 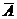имеет вероятность, близкую к единице, и наоборот. С другой стороны, непоявление события А означает появление противоположного события 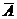. Таким образом, получено важное для приложений

Следствие. Если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании это событие наступит.

Замечание. Ответ на вопрос о том, какую вероятность считать близкой к единице, зависит от существа задачи.

Задача статистической проверки статистических гипотез

Виды статистических гипотез

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр 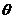равен определенному значению 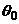, выдвигают гипотезу: 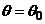. Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного рас­пределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок, о виде зависимости между величинами и многие другие.

Определение 1. Статистическойназывают гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Пример 2.1. Статистическими будут гипотезы:

1) генеральная совокупность распределена по закону Пуассона;

2) дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Определение 2. Нулевой (основной)называют выдвинутую гипотезу .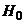

Определение 3. Конкурирующей (альтернативной)называют гипотезу 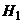,которая противоречит нулевой.

Пример 2.2. Если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что 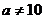. Коротко это записывают так: : ; : .

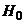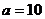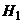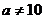Различают гипотезы, которые содержат только одно и более одного предположений.

Определение 4. Простойназывают гипотезу, содержащую только одно предположение.

Пример 2.3.1)Если 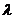– параметр показательного распределения, то гипотеза 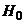: 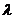=5 – простая. 2) Гипотеза 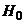:математическое ожидание нормального распределения равно 3 ( 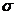известно) – простая.

Определение 5. Сложнойназывают гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Пример 2.4.1) Сложная гипотеза 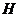: 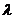>5 состоит из бесчисленного множества простых вида 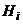: 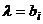, где 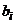– любое число, большее 5. 2) Гипотеза 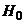: математическое ожидание нормального распределения равно 3 ( 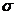неизвестно) – сложная.