Глава 4. Проверка статистических гипотез

Некоторые сводные характеристики выборки

Элементы вариационного ряда

Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда.

Определение 1. Равностоящиминазывают варианты , которые образуют арифметическую прогрессию с разностью h.

Определение 2. Условныминазывают варианты, определяемые равенством: 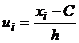, где С – ложный нуль (новое начало отсчёта), h – шаг, т.е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).

Замечание 1.Использование условных вариант позволяло упрощать расчёты характеристик выборки.

Замечание 2.Если вариационный ряд состоит из равноотстоящих вариант с шагом h, то условные варианты будет целыми числами.

Доказательство. Действительно, выберем в качестве ложного нуля произвольную варианту 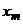, тогда 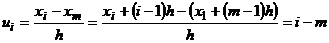– целое число.

Замечание 3.В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту). Варианте, принятой в качестве ложного нуля соответствует условная варианта, равная нулю.

Замечание 4.На практике, как правило, данные наблюдений не будут равноотстоящими числами. Естественно, возникает вопрос: нельзя ли соответствующей обработкой наблюдаемых значений признака свести вычисления к случаю равноотстоящих вариант? Оказывается, можно. С этой целью интервал, в котором заключены все наблюдаемые значения признака (первоначальные варианты), делят на несколько равных частичных интервалов. Практически в каждый частичный интервал должно попасть не менее 8-10 первоначальных вариант. Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант.

В качестве частоты каждой «новой» варианты (середины частичного интервала) принимают общее число первоначальных вариант, попавших в соответствующий частичный интервал.

Ясно, что замена первоначальных вариант серединами частичных интервалов сопровождается ошибками (первоначальные варианты левой половины частичного интервала будут увеличены, а варианты правой половины уменьшены), однако эти ошибки будут в основном погашаться, поскольку они имеют разные знаки.

Эмпирические моменты

Определения эмпирическим моментам аналогичны определениям теоретических моментов, введённых в теме «Случайные величины». В отличие от теоретических моментов, эмпирические моменты находят по данным наблюдений.

Определение 3. Обычным эмпирическим моментом порядка k называют среднее значение k-x степеней разностей 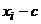: 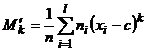, где – наблюдаемая варианта, 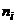– частота варианты, 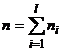– объём выборки, с – произвольное постоянное число (ложный нуль).

Определение 4. Начальным эмпирическим моментом порядка k называют обычный момент порядка k при с=0: .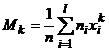

Замечание 5. В частности, .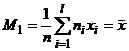

Определение 5. Центральным эмпирическим моментом порядка k называют обычный момент порядка k при : .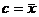

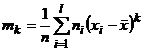Замечание 6.В частности 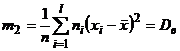.