Программа по высшей математике
Вопросы к экзамену по курсу «Высшая математика» для М и УП
1. Алгебраическое дополнение.
2. Минор матрицы.
3. Обратные матрицы.
4. Ранг матрицы. Элементарные преобразования матриц.
5. Решение систем линейных уравнений методом Гаусса.
6. Собственные векторы и собственные значения матриц.
7. Прямоугольная и полярная системы координат на плоскости.
8. Длина вектора. Угол между векторами.
9. Ортогональные и ортонормированные векторы.
10. Уравнения прямой на плоскости.
11. Расстояние между точками.
12. Деление отрезка в заданном отношении.
13. Линии второго порядка на плоскости.
14. Комплексные числа. Сумма, произведение, частное, возведение в степень, извлечение корня.
15. Замечательные пределы: 1-й, 2-й, 3-й.
16. Теорема Коши.
17. Теорема Ферма.
18. Теорема Ролля.
19. Теорема Лагранжа.
20. Определение непрерывности функции в точке и на промежутке.
21. Непрерывность элементарных функций.
22. Классификация разрывов.
23. Определение производной. Геометрический смысл производной.
24. Теорема о дифференцируемости и непрерывности функции.
25. Основные формулы и правила дифференцирования.
26. Производная сложной функции.
27. Производная степенно-показательной функции.
28. Дифференцирование функций, заданных параметрически.
29. Дифференциалы высших порядков.
30. Условие монотонности функции.
31. Выпуклость и выгнутость графика функции. Точки перегиба.
32. Асимптоты графика функции.
33. Необходимые условия существования максимума и минимума функций.
34. Достаточные условия существования экстремума функций.
35. Экстремумы функций нескольких переменных.
36. Раскрытие неопределенности вида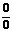 
. Теорема 1 Лопиталя (при 
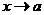, при 
).
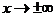37. Раскрытие неопределенности вида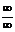 
. Теорема 2 Лопиталя 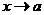(при , при ).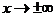
38. Раскрытие неопределенности вида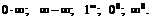 
39. Формула Тейлора и формула Маклорена для многочлена.
40. Разложение произвольной функции по формуле Тейлора.
41. Разложение элементарных функций по формуле Тейлора.
42. Свойства неопределенных интегралов.
43. Интегрирование рациональных выражений. Простые дроби, правильные дроби и их интегрирование.
44. Основная формула интегрального исчисления. Формула замены переменной в определенном интеграле.
45. Несобственные интегралы. Сходимость несобственных интегралов. Понятие абсолютной и условной сходимости несобственных интегралов.
46. Нахождение площади плоской фигуры и объема тела вращения.
47. Нахождение длины дуги и площади поверхности тела вращения.
48. Комбинаторика. Размещения, размещения с повторением.
49. Комбинаторика. Перестановки, перестановки с повторением.
50. Комбинаторика. Сочетания, сочетания с повторением.
51. Понятие вероятности. Классификация событий. Примеры.
52. Операции над вероятностями. Условная вероятность и её вычисление
53. Формула полной вероятности
54. Формула Байеса.
55. Случайные величины дискретные и непрерывные. Законы распределения случайных величин.
56. Закон нормального распределения.
57. Математическое ожидание, дисперсия случайной величины.
58. Корреляция. Коэффициент корреляции.
Обязательный минимум знаний
1. Операции над матрицами. Умножение матриц.
2. Транспонированные матрицы.
3. Определители матриц (2х2 и 3х3).
4. Нахождение минора матрицы.
5. Приведение матрицы к ступенчатому виду.
6. Решение систем линейных уравнений методом Гаусса.
7. Нахождение предела числовой последовательности.
8. Нахождение несложных пределов функций.
9. Формула расстояния между точками (решение задач)
10. Деление отрезка пополам (решение задач)
11. Вычисление производных (в том числе – производ. сложной функции и производ. высших порядков).
12. Интегрирование рациональных выражений. Простые дроби и их интегрирование.
13. Интегрирование путем замены переменной.
14. Несобственные интегралы – решение простых примеров.
15. Выпуклость и выгнутость графика функции. Точки перегиба. Асимптоты графика функции.
16. Наибольшие и наименьшие значения функций.
17. Условие монотонности функции.
18. Решение элементарных задач по теории вероятностей и по комбинаторике.
Дифференциальное исчисление
· Производная и дифференциал.
· Основные формулы и правила дифференцирования.
· Основные теоремы о дифференцируемых функциях и их приложения.
· Производные и дифференциалы функций нескольких переменных.
· Производные высших порядков.
· Дифференциалы высших порядков.
· Применение дифференциала функции для приближенных вычислений.
Интегральное исчисление
· Первообразная. Неопределенный интеграл и его свойства. Методы интегрирования. Использование таблиц интегралов.
· Определенный интеграл. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов.
· Двойной и тройной интегралы, их свойства. Вычисление кратных интегралов повторным интегрированием.
· Несобственные интегралы. Сходимость несобственных интегралов.
· Классические методы оптимизации. Функции спроса и предложения. Функция полезности. Кривые безразличия.
Линейная алгебра
· Системы линейных уравнений.
· Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.
· Определители. Системы векторов, ранг матрицы.
· N-мерное линейное векторное пространство. Евклидово пространство.
· Линейные операторы и матрицы. Собственные векторы и собственные значения линейных операторов.
· Квадратичные формы.
· Системы линейных неравенств. Симплексный метод.
· Линейные задачи оптимизации. Основные определения и задачи линейного программирования. Теория двойственности. Дискретное программирование. Динамическое программирование. Нелинейное программирование.
Элементы высшей алгебры
· Комплексные числа, действия с ними. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа.
· Алгебраическая и тригонометрическая формы записи комплексного числа. Формула Эйлера. Формула Муавра. Показательная форма записи комплексного числа. Возведение в степень, извлечение корня n-ой степени из комплексного числа. Решение квадратного уравнения.
Вопросы к экзамену по курсу «Высшая математика» для М и УП
1. Алгебраическое дополнение.
2. Минор матрицы.
3. Обратные матрицы.
4. Ранг матрицы. Элементарные преобразования матриц.
5. Решение систем линейных уравнений методом Гаусса.
6. Собственные векторы и собственные значения матриц.
7. Прямоугольная и полярная системы координат на плоскости.
8. Длина вектора. Угол между векторами.
9. Ортогональные и ортонормированные векторы.
10. Уравнения прямой на плоскости.
11. Расстояние между точками.
12. Деление отрезка в заданном отношении.
13. Линии второго порядка на плоскости.
14. Комплексные числа. Сумма, произведение, частное, возведение в степень, извлечение корня.
15. Замечательные пределы: 1-й, 2-й, 3-й.
16. Теорема Коши.
17. Теорема Ферма.
18. Теорема Ролля.
19. Теорема Лагранжа.
20. Определение непрерывности функции в точке и на промежутке.
21. Непрерывность элементарных функций.
22. Классификация разрывов.
23. Определение производной. Геометрический смысл производной.
24. Теорема о дифференцируемости и непрерывности функции.
25. Основные формулы и правила дифференцирования.
26. Производная сложной функции.
27. Производная степенно-показательной функции.
28. Дифференцирование функций, заданных параметрически.
29. Дифференциалы высших порядков.
30. Условие монотонности функции.
31. Выпуклость и выгнутость графика функции. Точки перегиба.
32. Асимптоты графика функции.
33. Необходимые условия существования максимума и минимума функций.
34. Достаточные условия существования экстремума функций.
35. Экстремумы функций нескольких переменных.
36. Раскрытие неопределенности вида 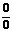. Теорема 1 Лопиталя 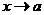(при , при ).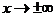
37. Раскрытие неопределенности вида 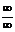. Теорема 2 Лопиталя 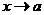(при , при ).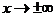
38. Раскрытие неопределенности вида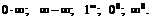
39. Формула Тейлора и формула Маклорена для многочлена.
40. Разложение произвольной функции по формуле Тейлора.
41. Разложение элементарных функций по формуле Тейлора.
42. Свойства неопределенных интегралов.
43. Интегрирование рациональных выражений. Простые дроби, правильные дроби и их интегрирование.
44. Основная формула интегрального исчисления. Формула замены переменной в определенном интеграле.
45. Несобственные интегралы. Сходимость несобственных интегралов. Понятие абсолютной и условной сходимости несобственных интегралов.
46. Нахождение площади плоской фигуры и объема тела вращения.
47. Нахождение длины дуги и площади поверхности тела вращения.
48. Комбинаторика. Размещения, размещения с повторением.
49. Комбинаторика. Перестановки, перестановки с повторением.
50. Комбинаторика. Сочетания, сочетания с повторением.
51. Понятие вероятности. Классификация событий. Примеры.
52. Операции над вероятностями. Условная вероятность и её вычисление
53. Формула полной вероятности
54. Формула Байеса.
55. Случайные величины дискретные и непрерывные. Законы распределения случайных величин.
56. Закон нормального распределения.
57. Математическое ожидание, дисперсия случайной величины.
58. Корреляция. Коэффициент корреляции.
Обязательный минимум знаний
1. Операции над матрицами. Умножение матриц.
2. Транспонированные матрицы.
3. Определители матриц (2х2 и 3х3).
4. Нахождение минора матрицы.
5. Приведение матрицы к ступенчатому виду.
6. Решение систем линейных уравнений методом Гаусса.
7. Нахождение предела числовой последовательности.
8. Нахождение несложных пределов функций.
9. Формула расстояния между точками (решение задач)
10. Деление отрезка пополам (решение задач)
11. Вычисление производных (в том числе – производ. сложной функции и производ. высших порядков).
12. Интегрирование рациональных выражений. Простые дроби и их интегрирование.
13. Интегрирование путем замены переменной.
14. Несобственные интегралы – решение простых примеров.
15. Выпуклость и выгнутость графика функции. Точки перегиба. Асимптоты графика функции.
16. Наибольшие и наименьшие значения функций.
17. Условие монотонности функции.
18. Решение элементарных задач по теории вероятностей и по комбинаторике.
Программа по высшей математике