Суммы Дарбу и интегрируемость функции по Риману.
Теорема:
Функция 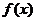 интегрируема на отрезке
интегрируема на отрезке 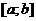 тогда и только тогда, когда
тогда и только тогда, когда 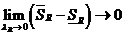 .
.
Доказательство:
Докажем необходимость условия:
Функция 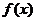 интегрируема на отрезке
интегрируема на отрезке 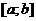 .
.
Пусть 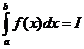 , тогда
, тогда 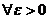
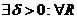
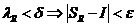 , т.е.
, т.е. 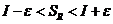 .
.
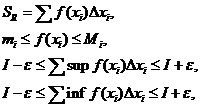
т.е. 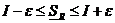 и
и 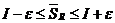 .
.
Далее имеем: 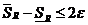 , т.е.
, т.е. 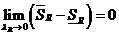 .
.
Необходимость доказана.
Докажем достаточность условия:
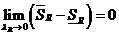 .
.
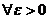
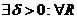
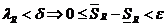 .
.
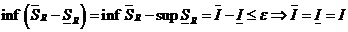 .
.
Докажем, что 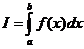 .
.
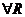
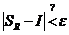 ,
,
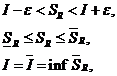
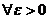
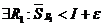 ,
,
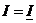 , тогда
, тогда 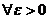
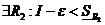 , т.е.
, т.е. 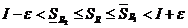 ,
,
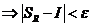 .
.
Достаточность доказана.
Билет 41
Основная теорема о существовании определенного интеграла Римана.
Теорема (Основная)
Ограниченная функция f интегрируема на отрезке [a,b] тогда и только тогда, когда 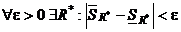 .
.
Доказательство:
 По теореме об интегрируемости (f интегрируема Û
По теореме об интегрируемости (f интегрируема Û 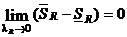 ) функция интегрируема тогда и только тогда, когда
) функция интегрируема тогда и только тогда, когда 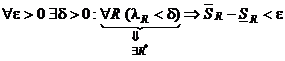 (1). Надо доказать, что если
(1). Надо доказать, что если 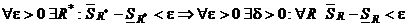 . Т.е. если найдется одно R*, удовлетворяющее неравенству (1), то оно (неравенство) будет выполняться для всех R. Возьмем произвольное
. Т.е. если найдется одно R*, удовлетворяющее неравенству (1), то оно (неравенство) будет выполняться для всех R. Возьмем произвольное 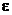 . Нужно найти δ, такое чтобы выполнялось неравенство
. Нужно найти δ, такое чтобы выполнялось неравенство 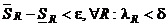 . По условию теоремы
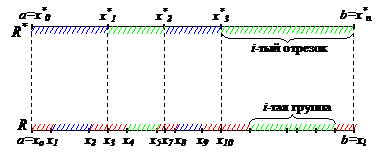
. По условию теоремы 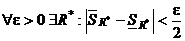 . Рассмотрим наше разбиение R* и произвольное R, как показано на рисунке. Составим разность верхней и нижней сумм Дарбý для нового разбиения R:
. Рассмотрим наше разбиение R* и произвольное R, как показано на рисунке. Составим разность верхней и нижней сумм Дарбý для нового разбиения R: 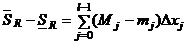 . Нужно сделать его меньше
. Нужно сделать его меньше 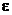 . Из условия имеем
. Из условия имеем 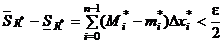 . Обозначим через Σ первую сумму и разобъем ее: Σ=Σ1+Σ2. Σ1 – такие слагаемые, что элемент нового разбиения R содержит в себе хотя бы одну точку границы старого раазбиения R*. Все остальное войдет в Σ2. Рассмотрим отдельно Σ1 и Σ2:
. Обозначим через Σ первую сумму и разобъем ее: Σ=Σ1+Σ2. Σ1 – такие слагаемые, что элемент нового разбиения R содержит в себе хотя бы одну точку границы старого раазбиения R*. Все остальное войдет в Σ2. Рассмотрим отдельно Σ1 и Σ2:
Σ1: 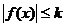 т.к. функция f – ограничена (k - константа). Тогда
т.к. функция f – ограничена (k - константа). Тогда 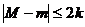 (M и m – максимум и минимум на [a,b]). Получим Σ1
(M и m – максимум и минимум на [a,b]). Получим Σ1 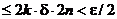 , где λR<δ, а количество красных отрезков не превосходит 2n. Для того чтобы это неравенство выполнялось, достаточно взять δ<
, где λR<δ, а количество красных отрезков не превосходит 2n. Для того чтобы это неравенство выполнялось, достаточно взять δ< 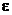 /8kn. Т.е. при δ<
/8kn. Т.е. при δ< 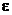 /8kn Σ1<
/8kn Σ1< 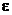 /2.
/2.
Σ2: разобъем Σ2 на повторные суммы, т.е. Σ2=Σ(Σi). Σi≤ 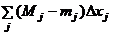 ≤
≤ 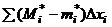 (Mi*-mi*)ΣΔxi*, где Mj и mj – максимум и минимум на j-том участке. Σi – группировка тех новых j-тых участков, которые попали в один и тот же старый. Получим Σ2
(Mi*-mi*)ΣΔxi*, где Mj и mj – максимум и минимум на j-том участке. Σi – группировка тех новых j-тых участков, которые попали в один и тот же старый. Получим Σ2 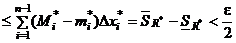 ÞΣ1+Σ2<ε, т.е. Σ<
ÞΣ1+Σ2<ε, т.е. Σ< 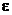 . В итоге:
. В итоге:
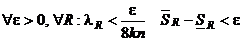 . Теорема доказана.
. Теорема доказана.
Следствие 1: Функция f – интегрируема на [a,b], если 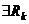 с
с 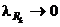 :
: 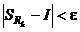 (если существует такая последовательность разбиений с мелкостью, стремящейся к нулю, что модуль разности последовательности интегральных сумм и интеграла стремится к нулю).
(если существует такая последовательность разбиений с мелкостью, стремящейся к нулю, что модуль разности последовательности интегральных сумм и интеграла стремится к нулю).
Следствие 2: Функция f – интегрируема на [a,b], если 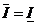 (если верхний интеграл равен нижнему).
(если верхний интеграл равен нижнему).
Билет 42
Равномерная непрерывность функции. Модуль непрерывности.
Определение 1: 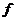 ограниченная
ограниченная 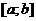 функция,
функция, 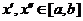 и
и 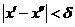 при выполнении условия
при выполнении условия 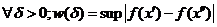 ,
, 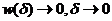 называется равномерно непрерывной.
называется равномерно непрерывной.
Определение 2(Критерий Коши): 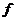 - равномерно непрерывная функция на отрезке
- равномерно непрерывная функция на отрезке 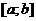 если выполняется условие
если выполняется условие 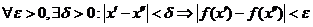 при
при 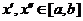 .
.
Теорема 1 (Эквивалентность определений 1 и 2)
Доказательство:
Так как 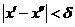 и
и 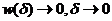 выполняется Критерий Коши.
выполняется Критерий Коши.
Теорема 2
Функция непрерывная на отрезке, равномерно непрерывна на нем ( 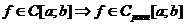 ).
).
Доказательство:
Допустим что теорема неверна. Построим отрицание к определению 2.
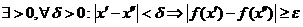 . Зададим стремящуюся к нулю последовательность положительных чисел
. Зададим стремящуюся к нулю последовательность положительных чисел  , тогда
, тогда 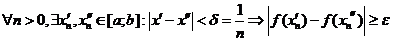 . Так как точки последовательности
. Так как точки последовательности  принадлежат к отрезку
принадлежат к отрезку 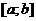 , то эта последовательность ограничена, и из нее можно выделить, по теореме Больцано-Вейерштрасса, подпоследовательность
, то эта последовательность ограничена, и из нее можно выделить, по теореме Больцано-Вейерштрасса, подпоследовательность 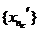 , сходящуюся к некоторой точке
, сходящуюся к некоторой точке 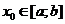 . Значит, из нее можно выделить также подпоследовательность
. Значит, из нее можно выделить также подпоследовательность 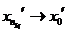 . Аналогично выделим подпоследовательность
. Аналогично выделим подпоследовательность 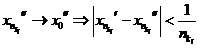 и
и 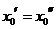
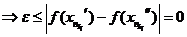 . Получили противоречие – теорема доказана.
. Получили противоречие – теорема доказана.
Необходимость условия: Если 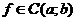 , то теорема 2 не выполняется.
, то теорема 2 не выполняется.
Пример 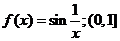 Пусть
Пусть  при
при 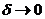 .
.
Билет 43
