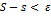Вопрос 3-5 Необх и дост усл интегрируемости. Верхн и нижн суммы Дарбу. Св-ва
Вопрос 1 Опр. инт-л Римана
Пусть дан  . Разбиением T отрезка
. Разбиением T отрезка  называется набор точек
называется набор точек 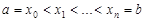 или набор отрезков
или набор отрезков 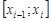 , где
, где 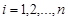 . Будем обозначать
. Будем обозначать 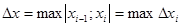 .
.
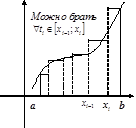 Пусть на отрезке
Пусть на отрезке  задана функция
задана функция 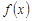 . Возьмём некоторое разбиение
. Возьмём некоторое разбиение 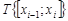 отрезка
отрезка  и в каждом отрезке
и в каждом отрезке 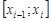 выберем точку
выберем точку 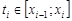 . Сумма
. Сумма 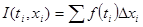 называется интегральной. Число I называется интегралом от
называется интегральной. Число I называется интегралом от 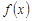 , если для
, если для 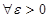
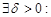 для всех разбиений T с
для всех разбиений T с 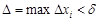 при любом выборе точек
при любом выборе точек 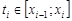 будет
будет 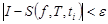 (т.е.
(т.е. 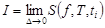 ). Обозначается
). Обозначается 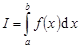 (интеграл, определённый таким образом, называется интегралом Римана). Если
(интеграл, определённый таким образом, называется интегралом Римана). Если 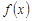 не ограничена на
не ограничена на  , то
, то 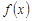 неинтегрируема на
неинтегрируема на  .
.
Вопрос 2 Основные определения
1. Неопределённый интеграл: Пусть ∆ - конечный или бесконеч. отрезок числ. оси, т.е. интервал, полуинтервал, или отрезок. На отрезке ∆ задана f(x) и F(x).
ОПР: Фун-я F(x) наз. первообразной ф-ции f(x) на ∆, если F’(x) дифф-ма на ∆ и F’(x)= f(x) для всех 
ОПР: Пусть f(x) определена на ∆. Совокупность всех ёё первообр. на ∆ наз-ся неопр. интегралом и обозн. 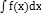
2. Определённый нтервал: см. Вопрос 1(инт-л Римана=опр. инт-л)
Вопрос 3-5 Необх и дост усл интегрируемости. Верхн и нижн суммы Дарбу. Св-ва
Изначально считаем, что 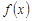 на
на  ограничена и пусть задано разбиение Т отрезка
ограничена и пусть задано разбиение Т отрезка  на отр.
на отр. 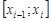 , где
, где 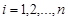 . На каждом из отрезков
. На каждом из отрезков 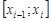 найдём Mi – точная верхняя грань и mi – точная нижн. грань ф-ции при х ε
найдём Mi – точная верхняя грань и mi – точная нижн. грань ф-ции при х ε 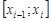
S= 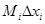 и s=mi
и s=mi 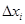 - соответственно верхняя и нижняя суммы Дарбу при разбиении T.
- соответственно верхняя и нижняя суммы Дарбу при разбиении T.
Свойства:
1. Любая интегр. ∑ заключена между верх. и нижн. ∑ Дарбу отвечающие данному разбиению Т.
2. Если к уже имеющ. точкам разбиения добавить ещё одну точку, то нижн. ∑ Дарбу может лишь возрасти, а верхняя – лишь уменьшиться.
3. Любая нижн. ∑ Дарбу не превосходит ∀ верх. ∑ Дарбу, если даже они отвечают различ. разбиениям  .
.
4. Множество всех нижн. ∑ Дарбу есть огран. сверху, напр. ∀ верхн. ∑, значит у этого мн-ва есть точная верхняя грань 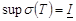
Множество всех верхн. ∑ Дарбу есть огран. снизу, напр. ∀ нижн. ∑, значит у этого мн-ва есть точная нижняя грань 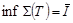
ТЕОР:Для существования опр. инт-ла необ. и дост, чтобы
1. Предел 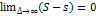
2. Чтобы для ∀ ε > 0: как только ∆< ẟ, то 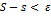
Вопрос 6 Классы интегрируемых функций
1. Если 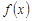 непрерывна на
непрерывна на  , то
, то 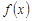 интегрируема на
интегрируема на  .
.
Док-во: Если f(x) непрерывна на  , то согласно теор. Кантора она равномерно непрерывна на этом отрезке. Это означает, что для
, то согласно теор. Кантора она равномерно непрерывна на этом отрезке. Это означает, что для 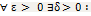 для любых
для любых 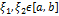 и
и 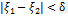 выполн. нер-во
выполн. нер-во 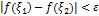
Возьмём 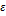 число
число 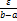 и выберем по нему такое разбиение отрезка чтобы
и выберем по нему такое разбиение отрезка чтобы 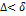 . Отсюда следует, что
. Отсюда следует, что 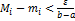

2. Если 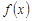 монотонна и ограничена на
монотонна и ограничена на  , то
, то 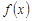 интегрируема на
интегрируема на  .
.
3. ОПР:Ф-ция наз. кусочно-непрерывной на  , если она имеет на этом отрезке конечн. число точек разрыва 1 рода, а в ост. точка она непрерывна.
, если она имеет на этом отрезке конечн. число точек разрыва 1 рода, а в ост. точка она непрерывна.
ТЕОР: кусочно-непрерывная на  ф-ция интегрируема на этом отрезке.
ф-ция интегрируема на этом отрезке.
Вопрос 8 Теорема о среднем значении
Пусть 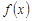 и
и 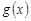 интегрируемы на
интегрируемы на 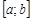 ,
, 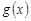 сохраняет знак на
сохраняет знак на 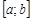 и
и 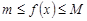 . Тогда
. Тогда 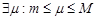 и
и 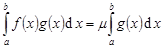 . Если, кроме того,
. Если, кроме того, 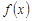 непрерывна на
непрерывна на 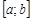 , то найдутся такие точки
, то найдутся такие точки 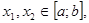 что f(x1) = m, f(x2) = M и число ή: f(ή) - µ и
что f(x1) = m, f(x2) = M и число ή: f(ή) - µ и 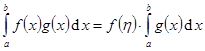 .
.
Вопрос 13 Несобственные инт-лы с беск. пределами и несобственные инт-лы от неогранич. ф-ций. Определения и признак сходимости.
Пусть 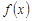 интегрируема на
интегрируема на 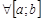 , и
, и 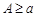 . Тогда
. Тогда 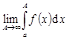 называется несобственным
называется несобственным 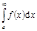 . Если этот предел существует и конечен, то говорят, что несобственный
. Если этот предел существует и конечен, то говорят, что несобственный 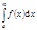 сходится. Примеры:
сходится. Примеры:
1. 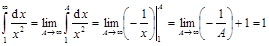 .
.
2. 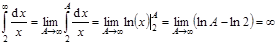 .
.
Аналогично, 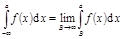 ,
, 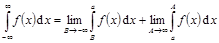 , где a – произвольное число.
, где a – произвольное число.
Пусть 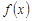 интегрируема на
интегрируема на 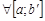 , где
, где 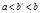 и в окрестности b
и в окрестности b 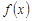 неограниченна. Тогда
неограниченна. Тогда 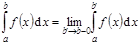 – несобственный интеграл.
– несобственный интеграл.
Примеры:
1. 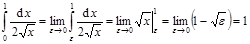 .
.
2. 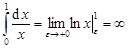 .
.
Признаки сходимости несоб. инт-ла
Вступление:
1. 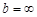 ,несобственный инт-л 1 рода.
,несобственный инт-л 1 рода.
2. b – конечное число, а 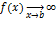 – несобственный инл 2 рода.
– несобственный инл 2 рода.
Признаки сходимости несоб. инт-ла для f(x)>0 ∀ 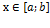 :
:
1)Признак сравнения (с нер-вами)
1. 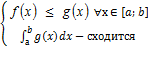 =>
=> 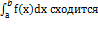
2. 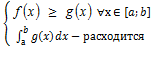 =>
=> 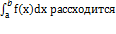
2) Признак сравнения (с  )
) 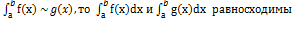
Вопрос 26 Степенные ряды. Радиус сх-ти и круг сх-ти, формулы Коши-Адамара и Даламбера для вычисления радиуса сх-ти. Почленнаядиф-ть и инт-ть степ.рядов. Ряды Тейлора, теорема о разложимости, степ.ряды элементарных ф-ций.
Степенными рядами называются ряды вида 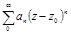 или
или 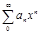 .Формула Коши-Адамара: Для любого степенного ряда
.Формула Коши-Адамара: Для любого степенного ряда 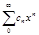 существует число
существует число 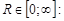 при
при 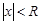 ряд сходится абсолютно, при
ряд сходится абсолютно, при 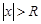 ряд расходится. Если R = 0, то ряд сходится только при x= 0. Если R = ¥, то ряд абсолютно расходится для "x. Это число R называется радиусом сходимости и может быть найдено по формуле:
ряд расходится. Если R = 0, то ряд сходится только при x= 0. Если R = ¥, то ряд абсолютно расходится для "x. Это число R называется радиусом сходимости и может быть найдено по формуле: 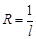 , где
, где 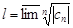 Док-во:Пусть RÎ (0;¥), т.е. lÎ (0;¥). а) Возьмём сначала
Док-во:Пусть RÎ (0;¥), т.е. lÎ (0;¥). а) Возьмём сначала 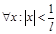 , т.е.
, т.е. 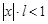 . Тогда существует достаточно малое
. Тогда существует достаточно малое 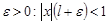 . По определению
. По определению 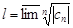 правее l + e может быть только конечное число
правее l + e может быть только конечное число 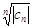 , т.е. $N:для "n>N будет
, т.е. $N:для "n>N будет 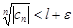 . Тогда для
. Тогда для 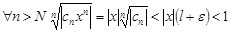 , откуда по радикальному признаку Коши
, откуда по радикальному признаку Коши 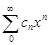 сходится абсолютно для
сходится абсолютно для 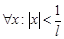 .б) Возьмём теперь
.б) Возьмём теперь 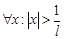 , т.е.
, т.е. 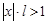 . Тогда существует достаточно малое
. Тогда существует достаточно малое 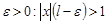 . По определению
. По определению 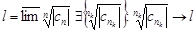 . Тогда $K: для "k>K будет
. Тогда $K: для "k>K будет 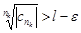 , значит
, значит 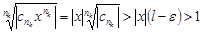 , откуда при
, откуда при 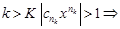 ряд расходится, т.к.
ряд расходится, т.к. 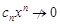 при n®¥.Пусть теперь R = ¥, т.е. l = 0, т.е.
при n®¥.Пусть теперь R = ¥, т.е. l = 0, т.е. 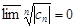 . Т.к.
. Т.к. 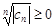 для "n, то все частичные пределы последовательности
для "n, то все частичные пределы последовательности 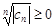 , а т.к. наибольший из них равен 0, то у
, а т.к. наибольший из них равен 0, то у 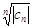 один частичный предел, т.е.
один частичный предел, т.е. 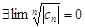 . Покажем, что для
. Покажем, что для 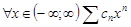 абсолютно сходится. Т.к.
абсолютно сходится. Т.к. 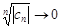 при n®¥, то $N: для "n>N будет
при n®¥, то $N: для "n>N будет 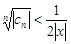 . Тогда
. Тогда 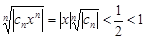 и по радикальному признаку Коши
и по радикальному признаку Коши 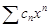 сходится абсолютно.Пусть, наконец, R = 0, т.е. l = ¥. Это значит, что
сходится абсолютно.Пусть, наконец, R = 0, т.е. l = ¥. Это значит, что 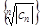 не ограничена сверху. Докажем, что для
не ограничена сверху. Докажем, что для 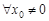 ряд
ряд 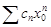 расходится. Предположим, что он сходится. Тогда
расходится. Предположим, что он сходится. Тогда 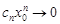 при n® 0. Тогда
при n® 0. Тогда 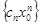 ограничена, т.е.
ограничена, т.е. 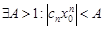 , откуд
, откуд 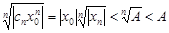 , а, значит,
, а, значит, 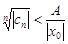 , т.е.
, т.е. 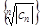 ограничена, что противоречит условию, следовательно,
ограничена, что противоречит условию, следовательно, 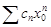 расходится.Для
расходится.Для 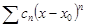 будет абсолютная сходимость при
будет абсолютная сходимость при 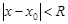 и расходимость при
и расходимость при 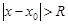 .Множество
.Множество 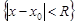 будем называть кругом сходимости.
будем называть кругом сходимости.
Различие между сходимостью и абсолютной сходимость у 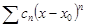 может быть только при
может быть только при 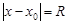 .На окружности
.На окружности 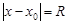 (в комплексной плоскости) возможны разные случаи.Пусть для
(в комплексной плоскости) возможны разные случаи.Пусть для 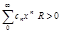 . Тогда в
. Тогда в 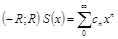 – непрерывная функция.Возьмём
– непрерывная функция.Возьмём 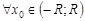 . Тогда
. Тогда 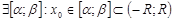 . На
. На 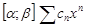 сходится равномерно. Все его члены
сходится равномерно. Все его члены 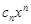 непрерывны, следовательно,
непрерывны, следовательно, 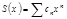 непрерывна на
непрерывна на 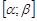 , в том числе в точке
, в том числе в точке 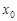 . Т.к. эта точка – любая из
. Т.к. эта точка – любая из 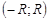 , то
, то 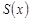 непрерывна на
непрерывна на 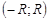 .
.
Диф и интегр. R сход степ ряда и а0+а1х+3а2х2+…ряда получ из него формальн диф-ния свпадает а1+2а2х+3а2х2+…Док-во: Пусть R сход степ ряда 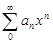 =R,R сход 2-го ряда=R1:
=R,R сход 2-го ряда=R1: 
2.Степ ряд 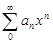 диф-ют в пределах открытого круга
диф-ют в пределах открытого круга 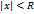 сх-ти
сх-ти 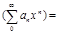
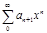 Т.К степ ряд сход на [-q;q], наход строго внутри и нтерв сход-ти, то степ ряд можно почленно
Т.К степ ряд сход на [-q;q], наход строго внутри и нтерв сход-ти, то степ ряд можно почленно 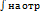 [x.x0]справ-ва ф-ла
[x.x0]справ-ва ф-ла 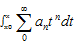 =
= 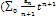 )|xx0=a0(x-x0)-
)|xx0=a0(x-x0)- 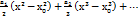 х0,х
х0,х 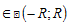
Ряд Тейлора.f(x) разлагатся в степ ряд, если найдутся такие числа аn, n=0123..., что f(x)= 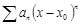 Теорема.Чтобыf(x) разлогалась в степ ряд, на инт-ле (x0-R,x0+R)необх и дост, чтобы она была в этом инт-ле и ост член в ф-ле Тейл к→0 при n→∞
Теорема.Чтобыf(x) разлогалась в степ ряд, на инт-ле (x0-R,x0+R)необх и дост, чтобы она была в этом инт-ле и ост член в ф-ле Тейл к→0 при n→∞
Разложения в ряд Тейлора:
Вопрос 1 Опр. инт-л Римана
Пусть дан  . Разбиением T отрезка
. Разбиением T отрезка  называется набор точек
называется набор точек 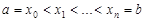 или набор отрезков
или набор отрезков 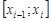 , где
, где 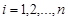 . Будем обозначать
. Будем обозначать 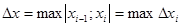 .
.
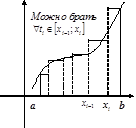 Пусть на отрезке
Пусть на отрезке  задана функция
задана функция 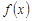 . Возьмём некоторое разбиение
. Возьмём некоторое разбиение 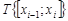 отрезка
отрезка  и в каждом отрезке
и в каждом отрезке 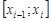 выберем точку
выберем точку 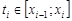 . Сумма
. Сумма 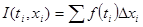 называется интегральной. Число I называется интегралом от
называется интегральной. Число I называется интегралом от 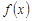 , если для
, если для 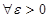
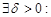 для всех разбиений T с
для всех разбиений T с 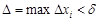 при любом выборе точек
при любом выборе точек 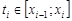 будет
будет 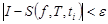 (т.е.
(т.е. 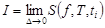 ). Обозначается
). Обозначается 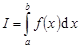 (интеграл, определённый таким образом, называется интегралом Римана). Если
(интеграл, определённый таким образом, называется интегралом Римана). Если 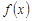 не ограничена на
не ограничена на  , то
, то 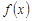 неинтегрируема на
неинтегрируема на  .
.
Вопрос 2 Основные определения
1. Неопределённый интеграл: Пусть ∆ - конечный или бесконеч. отрезок числ. оси, т.е. интервал, полуинтервал, или отрезок. На отрезке ∆ задана f(x) и F(x).
ОПР: Фун-я F(x) наз. первообразной ф-ции f(x) на ∆, если F’(x) дифф-ма на ∆ и F’(x)= f(x) для всех 
ОПР: Пусть f(x) определена на ∆. Совокупность всех ёё первообр. на ∆ наз-ся неопр. интегралом и обозн. 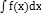
2. Определённый нтервал: см. Вопрос 1(инт-л Римана=опр. инт-л)
Вопрос 3-5 Необх и дост усл интегрируемости. Верхн и нижн суммы Дарбу. Св-ва
Изначально считаем, что 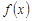 на
на  ограничена и пусть задано разбиение Т отрезка
ограничена и пусть задано разбиение Т отрезка  на отр.
на отр. 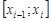 , где
, где 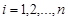 . На каждом из отрезков
. На каждом из отрезков 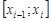 найдём Mi – точная верхняя грань и mi – точная нижн. грань ф-ции при х ε
найдём Mi – точная верхняя грань и mi – точная нижн. грань ф-ции при х ε 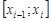
S= 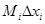 и s=mi
и s=mi 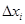 - соответственно верхняя и нижняя суммы Дарбу при разбиении T.
- соответственно верхняя и нижняя суммы Дарбу при разбиении T.
Свойства:
1. Любая интегр. ∑ заключена между верх. и нижн. ∑ Дарбу отвечающие данному разбиению Т.
2. Если к уже имеющ. точкам разбиения добавить ещё одну точку, то нижн. ∑ Дарбу может лишь возрасти, а верхняя – лишь уменьшиться.
3. Любая нижн. ∑ Дарбу не превосходит ∀ верх. ∑ Дарбу, если даже они отвечают различ. разбиениям  .
.
4. Множество всех нижн. ∑ Дарбу есть огран. сверху, напр. ∀ верхн. ∑, значит у этого мн-ва есть точная верхняя грань 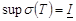
Множество всех верхн. ∑ Дарбу есть огран. снизу, напр. ∀ нижн. ∑, значит у этого мн-ва есть точная нижняя грань 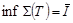
ТЕОР:Для существования опр. инт-ла необ. и дост, чтобы
1. Предел 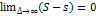
2. Чтобы для ∀ ε > 0: как только ∆< ẟ, то