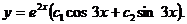Обыкновенные дифференциальные уравнения
Дифференциальные уравнения первого порядка. Основные понятия
[2, гл. XIII, § 2, 3, упр. 1-8].
Уравнение с разделенными и разделяющимися переменными
[2, гл. XIII, § 4, упр. 9-16].
Пример 1. Найти общее решение уравнения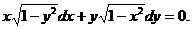 
Решение. Сначала определим вид дифференциального уравнения. Данное уравнение не является уравнением с разделенными переменными, так как коэффициенты при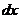 
и 
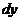зависят каждый от двух переменных. Но, разделив обе части уравнения на произведение 
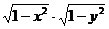(считая, что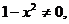 
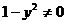), приведем его к виду
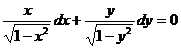
это уравнение с разделенными переменными.
Находим общее решение
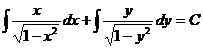
или
.
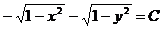Умножив обе части на (-1), включим знак “-“ в постоянную С. Решение примет вид
.
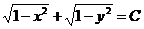Таким образом, нами получено общее решение заданного уравнения.
Однородные уравнения первого порядка
[2, гл. ХIII, § 5, упр. 39-46].
Пример 2. Найти общее решение уравнения
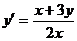. (1)
Решение. Определим вид этого уравнения. Это – однородное уравнение, поскольку его правая часть есть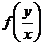 
.
Поделив почленно правую часть на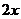 
, получим
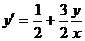
Делаем подстановку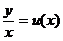 
или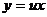 
. Тогда 
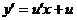и уравнение примет вид
. 
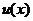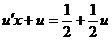(2)
Разделяем переменные
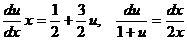
и интегрируем
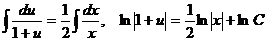
или после потенцирования
.
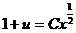Нами получено общее решение уравнения (2).
Чтобы найти общее решение уравнения (1), вернемся к старой переменной y. Подставим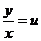 
, тогда будем иметь
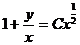или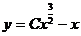 
.
Линейные уравнения первого порядка
[2, гл. ХIII, § 7, упр. 57-65].
Пример 3. Найти общее решение уравнения первого порядка
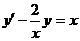
Решение. Определим вид этого уравнения. Уравнение вида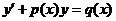 
называется линейным. Полагаем 
; 
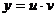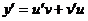и подставляем это в данное уравнение
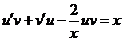
Группируем члены
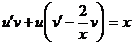
и полагаем
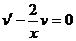(3)
Остается
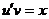. (4)
Находим сначала v из (3)
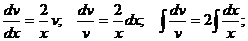
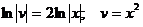
Заметим, что v не содержит никаких произвольных постоянных.
Подставляем v в (4) и получаем
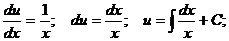
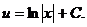
Окончательно получаем искомое общее решение
.
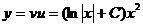Дифференциальные уравнения высших порядков. Основные понятия.
[2, гл. ХIII, § 16, 17, упр. 118-124].
Линейные однородные уравнения второго порядка
[2, гл.ХШ, § 20,21, упр. 129-137].
Пример 4. Найти общее решение уравнения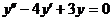 
.
Решение. Ищем решение уравнения в виде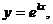 
тогда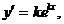 
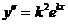и, подставляя в исходное уравнение получим 
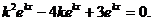Так как 
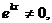то на него можно сократить и мы получим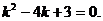 
Находим его корни
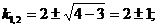
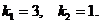
Корни характеристического уравнения вещественные, различные, значит, общее решение дифференциального уравнения имеет вид
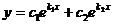
или 
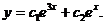
Пример 5. Найти общее решение уравнения
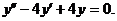
Решение. Составляем характеристическое уравнение (см. пример 9)
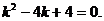
Решаем его
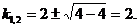
Корни характеристического уравнения вещественные равные. Общее решение дифференциального уравнения имеет вид
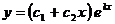
или
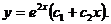
Пример 6. Найти общее решение уравнения
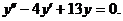
Решение. Составляем характеристическое уравнение (см. пример 9)
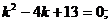
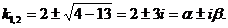
Корни характеристического уравнения комплексные сопряженные, значит, общее решение дифференциального уравнения имеет вид
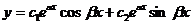
или
