Определение и свойства неопределенного интеграла

МАТЕМАТИКА

Методические указания и контрольные задания 3 и 4

для студентов-заочников 1-го курса

Методические указания и контрольные задания 3 и 4 для студентов заочной сокращенной формы обучения РИНПО

по направлениям:

26200062 - Технология изделий легкой промышленности по профилю «Технология швейных изделий»

262200.62 - Конструирование изделий легкой промышленности по профилю «Конструирование швейных изделий»

100800.62 - Товароведение

Составители Г. П. Мещерякова Е.В. Наумова

Санкт-Петербург

УТВЕРЖДЕНО

на заседании методической комиссии

Регионального института непрерывного обучения

протокол № 1 от 14. 09. 2012

Рецензент

Н. В. Дробатун

Оригинал подготовлен составителями и издан в авторской редакции

Подписано в печать11.10.12. Формат 60х84 1/16.

Усл. печ. л. 1,7_. Тираж _100_. Заказ 281/12

Электронный адрес: http://alt-rinpo.sutd.ru/

Отпечатано в типографии СПГУТД.

191028, Санкт - Петербург, ул. Моховая, 26

При выполнении контрольной работы на титульном листе указывается:

фамилия, имя, отчество;

номер студенческого билета;

название дисциплины, номер контрольной работы, номер варианта.

Номер варианта соответствует последней цифре номера студенческого билета.

Перечень контрольных заданий по методичке кафедры математики

КОНТРОЛЬНАЯ РАБОТА N 3 (методичка к/р 3,4)

Нечетный год поступления N 1(1 -10), 2(1 – 10), 3(1 – 10), 4(1 – 10).

Четный год поступления N 1(11 -20), 2(11 – 20), 3(11 – 20), 4(11 – 20).

КОНТРОЛЬНАЯ РАБОТА N 4 (методичка к/р 3,4)

Нечетный год поступления N 1 (1 -10), 2 (1 - 10), 3 (1 - 10), 4 (1 - 10), 5(1 - 10).

Четный год поступления N 1 (11 -20), 2 (11 - 20), 3 (11 - 20), 4 (11 - 20), 5(11 - 20).

Контрольная работа № 3

Неопределенный интеграл

Определение и свойства неопределенного интеграла

Литература. [1], гл. Х, §1-3, упр. 2, 5, 7, 9, 11, 14, 16, 17, 25, 41, 46, 49, 58, 60, 66.

Определенный интеграл

Определение, свойства и вычисление определенного интеграла

Литература.[1], гл.XI, § 1-5, 6 (пример можно пропустить), упр. 8, 10, 11, 13, 16-21, 23, 24.

Пример.Вычислить .

Решение. Так как интеграл от суммы функций равен сумме интегралов, то

Геометрические приложения определенного интеграла

Литература. [1], гл.XII, §1, упр. 1, 3, 5-11; §2, упр. 13, 14, 17, 18; §3, упр. 38-41, 43, 47; §4, 5, упр. 20-23, 25, 32; §6, упр. 49, 51, 53, 56.

Пример 1. Вычислить площадь фигуры, ограниченной линиями и .

Решение. Построим в системе координат эти линии. Найдем точки пересечения этих линий

Рис.1.

Обозначим эти точки через A и В. Итак, А(1; 5), В(5; 1). Искомая площадь S равна разности площадей фигур, ограниченных линиями , , , (обозначим эту площадь через S₁) и линиями , , , (эту площадь обозначим через S₂). Таким образом

S = S₁ – S₂

Площадь S₂ может быть вычислена с применением определенного интеграла

ед².

Площадь S₁ можно, конечно, вычислить как сумму площадей прямоугольного треугольника и прямоугольника, но удобнее все-таки вычислить S₁ как интеграл

.

Теперь можно вычислить и искомую площадь

S = S₁ – S₂ = 12 – 5 ln5

Ответ: S =12 – 5 ln5 ед².

Пример 2.Вычислить объем тела, полученного вращением вокруг оси О фигуры, ограниченной прямой и параболой .

Решение.Найдем точки пересечения линий. Для этого решим уравнение . Получим .

Рис. 2.

Объем тела может быть вычислен по формуле , где

, .

.

Ответ: .

Обыкновенные дифференциальные уравнения

Дифференциальные уравнения первого порядка. Основные понятия

[2, гл. XIII, § 2, 3, упр. 1-8].

Дифференциальные уравнения высших порядков. Основные понятия.

[2, гл. ХIII, § 16, 17, упр. 118-124].

Контрольная работа № 3. Задания.

1. Найти неопределенные и определенный интегралы. В двух первых примерах (п. а) и б) проверить результаты дифференцированием.

№	а	б	в	г
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.20

Контрольная работа №4

Ряды

1. Основные определения

[2, гл. ХVI, § 1, 2, упр. 1-5].

Функциональные ряды

[2, гл. XVI, § 9 - 12].

Степенные ряды

[2, гл. XVI, § 13, упр. 30, 31, 35-37].

Пример. Определить интервал сходимости ряда

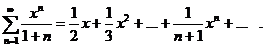
Решение. Коэффициенты ряда 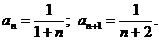Ищем радиус сходимости

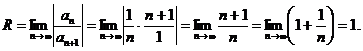
Следовательно, ряд сходится при 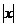<1 и расходится при 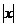>1. Исследуем отдельно точки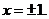

1) 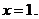В этой точке ряд равен

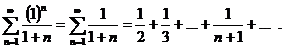
Используем интегральный признак сходимости. Заменим 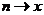. Тогда

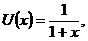
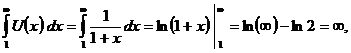
ряд расходится.

2) 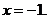В этой точке ряд равен

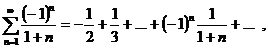
т.е. ряд знакочередующийся. По теореме Лейбница он сходится, действительно, здесь

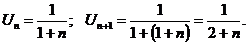
1) 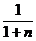> 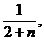т.е. > .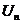

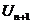2)

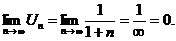
Ряд сходится. Интервал сходимости 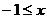< 1 или .

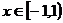Ряды Тейлора и Маклорена

[2, гл. XVI, § 16, 17, 19, 20, упр. 50, 51, 54-57.

Теория вероятностей.

Теория соединений

Теория соединений или комбинаторика рассматривает различные наборы множества элементов, выбранных из некоторого исходного набора множества этих элементов. Эти наборы составляются по определенным правилам и называются соединениями. Природа элементов, входящих во множество может быть любой, например, какие-то предметы, или люди, или числа и т.п. Нас, прежде всего, будет интересовать вопрос: сколько различных соединений можно составить? Рассмотрим самое простое соединение. Пусть исходное множество элементов разбито на k групп (наборов), содержащих n₁ , n₂ , ... , n_k элементов, т.е. первый набор n₁ элементов, второй n₂ элементов и т.д. Чтобы составить соединение из каждого набора следует взять один элемент. Сколько различных соединений можно составить? Очевидно каждый элемент первого набора может встретиться в соединении с каждым элементом второго набора и таких пар будет n₁n₂ . Каждая такая пара может встретиться с каждым элементом третьего набора, т.е. разных троек уже будет n₁n₂n₃ . Если обозначить за N число всех возможных соединений по одному элементу из каждого из k наборов, то получим

N = n₁ ∙ n₂ ∙ ... n_k .

Пример 1. В некотором городе телефонные номера состоят из буквы и пяти цифр. Буква может быть только А, В или Г. Первая цифра бывает 2, 3 , 4 или 5, а остальные цифры могут быть любые. Сколько телефонов может быть установлено в этом городе?

Решение. Первый набор состоит из трех букв, т.е. n₁ = 3 , второй - из четырех цифр, n₂ = 4. Следующие четыре набора содержат по 10 цифр, т.е. n₃ = n₄ = n₅ = n₆ = 10. Тогда всего различных номеров может быть N = 3´4´10´10´10´10 = 120 000.

В частном случае, если все k наборов содержат одинаковое количество элементов, скажем по n, то

N = n^k

Пример 2.Бросают две игральных кости. Сколько различных пар чисел может выпасть? (Нужно учесть, что 1 на первой кости и 2 на второй или 2 на первой и 1 на второй - это разные пары, т.е. разные соединения).

Решение. Так как у игральной кости, имеющей форму кубика, шесть граней, то n = 6, поэтому N = 6² = 36.

Отметим, что такие соединения могут получаться и в том случае когда имеется один набор из n элементов, из которого берут элемент, записывают его характеристику и возвращают в набор, после чего выбирают следующий элемент. В этом случае один и тот же элемент как бы выбирается из нового, но такого же как предыдущий, набора.

Теперь представим себе, что взятый один раз элемент обратно в набор не возвращается. Тогда второй элемент выбирается уже из набора, содержащего n - 1 элемент, третий из набора, содержащего n - 2 элемента и т.д. Это уже новый вид соединения, называемый размещением из n элементов по k элементов. Число размещений обозначается буквой А с двумя индексами

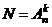
и читается “ а из эн по ка”

Каждое размещение отличается от другого или входящими элементами или их порядком. Например, из трех элементов a, b, c можно составить 6 размещений по 2 элемента ab, ac, bc, ba, ca, cb

Число различных размещений определяется формулой

.

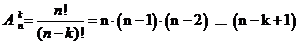Пример 3.В группе из 20 человек проводиться собрание. Сколькими способами можно избрать председателя, его заместителя и секретаря?

Решение. Очевидно, что важно не только кого изберут, но и на какие должности. Поэтому одно соединение от другого может отличаться или составом или порядком, т.е. это размещения, поэтому

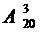= 20´19´18 = 6840

Если составлять размещения из всех n элементов, то очевидно они будут отличаться только порядком. Такие соединения называются перестановками из n элементов. Число перестановок обозначается P_n (“пэ из эн”) и, очевидно получается из 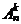при k = n, т.е.

P_n = n∙(n-1)∙(n-2) ... (n-n+1) = 1´2´3´…´n! = n! (“эн факториал”).

Пример 4.На трех карточках написаны цифры 1, 2, 3. Сколько различных трехзначных чисел можно составить переставляя местами эти карточки?

Решение. Очевидно, это число перестановок из трех, т.е.

Р₃ = 3! = 1´2´3 = 6.

Теперь рассмотрим соединения, которые называются сочетаниями из n элементов по k элементов. Это такие соединения, содержащие k элементов, взятых из данного множества из n элементов, которые отличаются только самими элементами (порядок роли не играет). Например, n = 3 : a, b, c , k = 2 тогда можно составить три сочетания ab, ac, bc. ( ab и ba - это разные размещения, но одно и то же сочетание). Число сочетаний обозначается буквой С. Очевидно, что для того чтобы составить все размещения нужно составить все возможные сочетания и в каждом произвести все возможные перестановки:

,

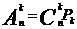где 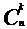- число сочетаний из n элементов по k элементов (“цэ из эн по ка”). Тогда

.

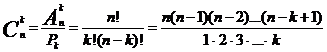Пример 5.На том же собрании 20 человек, где избирали председателя, заместителя и секретаря, нужно выбрать делегацию на конференцию в составе трех человек.

Решение. В этом случае порядок роли не играет, поэтому это не размещения, а сочетания и мы имеем

.

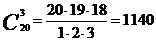Приведенные формулы числа размещений и числа сочетаний удобны для решения задач с конкретными числами n и k. Если задача решается в общем виде, то лучше пользоваться более компактными записями через факториалы, очень удобно ввести два определения

0!=1 и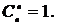

Событие и вероятность

[3. Введение, ч.1, гл.1, § 1 – 6].

Пример 1. В ящике 5 белых и 4 черных шара. Наудачу вынимают три. Какова вероятность, что среди них два белых и один черный шар?

Решение. Число всех возможных исходов - это число сочетаний из 9 по 3. Поэтому

.

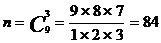Число вариантов выбора 2 белых из 4 белых - это число сочетаний из 4 по 2, то есть

,

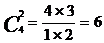и так как каждая пара может выпасть с любым из 4 черных шаров, то число благоприятных исходов равно произведению

m = 6∙4 = 24.

Тогда вероятность события “из ящика взяли 2 белых и 1 черный шар”

.

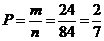Пример 2. На 10 карточках написаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Наудачу выбирают три карточки и раскладывают их в порядке появления. Какова вероятность, что получится число 120?

Решение. Поскольку в этом примере важен порядок цифр, то число всех возможных исходов

.

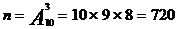Благоприятный исход только один, поэтому искомая вероятность

P .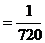

Контрольная работа № 4. Задания.

1. Определить область сходимости ряда:

1.1.	1.11.
1.2.	1.12.
1.3.	1.13.
1.4.	1.14.
1.5.	1.15.
1.6.	1.16.
1.7.	1.17.
1.8.	1.18.
1.9.	1.19.
1.10.	1.20.

Случайные события.

3.1.В цепь последовательно включены три независимо работающих элемента с вероятностями отказа соответственно 0,1; 0,15 и 0,2. Какова вероятность того, что по цепи ток не идет?

3.2.Для одной торпеды вероятность потопить корабль равна ½. Какова вероятность того, что четыре торпеды потопят корабль, если для потопления корабля достаточно одного попадания торпеды в цель?

3.3.Одновременно подбрасывают монету и игральную кость. Если на монете выпал герб, то выигрыш составляет 0 очков, а если решка - 2 очка. Эти очки суммируются с очками на кубике. Найти вероятность того, что суммарный выигрыш на кости и монете составит четыре очка.

3.4.Вероятность того, что можно выбить 10 очков на данной дистанции для данного стрелка при одном выстреле, равна 0,1, девять очков – 0,3. Какова вероятность того, что при трех выстрелах будет выбито более 27 очков?

3.5.Вероятность выигрыша на один билет 0,13. Какова вероятность хотя бы одного выигрыша для владельца пяти билетов/

3.6. Для игрока равновероятны все три исхода каждой партии (выигрыш, ничья, проигрыш). Найти вероятность того, что из четырех партий он а) не проиграет ни одного; б) проиграет хотя бы одну.

3.7.Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания первым, вторым и третьим стрелком равны соответственно 0,6; 0,5 и 0,4.

3.8.На склад поступает 60% продукции с первого участка и 40% со второго, причем с первого – 80% изделий первого сорта, а со второго – 75%. Какова вероятность того, что наудачу взятое изделие изготовлено на втором участке, если оно первого сорта.

3.9.Для контроля продукции, состоящей из пяти партий, отобрано наудачу одно изделие. Какова вероятность обнаружить брак, если в одной из партий деталей браковано, а в остальных четырех все годные.

3.10.Узел состоит из двух независимо работающих деталей, исправность каждой необходима для работы узла. Первая из деталей за рассматриваемый промежуток времени остается годной с вероятностью 0,8, а вторая – 0,9. Узел вышел из строя. Какова вероятность того, что это произошло из-за неисправности лишь второй детали ?

3.11.Рабочий обслуживает три станка. Вероятность выхода из строя за смену для них, соответственно, равна 0,75; 0,8 и 0,7. Найти вероятность того, что за смену выйдут из строя точно два станка.

3.12.Для игрока равновероятны все три исхода каждой партии (выигрыш, ничья, проигрыш). Найти вероятность того, что из четырех партий он а) не проиграет ни одного; б) проиграет хотя бы одну.

3.13.Студент сдает зачет, причем получает один вопрос из трех разделов. Первые два раздела одинаковы по объему, а третий в два раза больше первого. Студент знает ответы на 70% вопросов первого раздела, на 50% вопросов второго и на 80% вопросов третьего. Студент зачет сдал. Найти вероятность того, что ему попался вопрос из второго раздела.

3.14.Вероятность того, что деталь изготовленная на первом станке будет первосортной равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, а на втором – три. Найти вероятность того, что все детали первосортные.

3.15.В двух партиях изделий из 15 и 20 штук по 2 изделия бракованных. Из наудачу взятой партии выбрано одно изделие. Какова вероятность того, что оно бракованное?

3.16.В тире имеются пять ружей, вероятности попадания из которых равны 0,5; 0,6; 0,7; 0,8 и 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет ружье наудачу.

3.17.Стрелок стреляет по мишени, которая состоит из круга и двух концентрических колец. Вероятность попадания в круг и кольца соответственно равны 0,2; 0,15; и 0,1. Определить вероятность попадания в мишень.

3.18.Хлопок смешан с вискозой в пропорции 1:2. Какова вероятность того, что в случайном соединении трех волокон два окажутся вискозными?

3.19. Студент - прогульщик может подняться в библиотеку либо на лифт, либо пешком. Вероятность встретиться с преподавателем в лифте 0,6, а на лестнице - 0,7. Найти вероятность того, что он избежит нежелательной встречи с преподавателем.

3.20.В порту ожидается прибытие трех судов с фруктами. Известно, что в 1% случаев груз начинает портиться в дороге. Найти вероятность того, что в порт прибудут с испорченным грузом а) два судна; б) менее двух судов.

Библиографический список

1. Пискунов Н.С.Дифференциальное и интегральное исчисления. Т. 2. - М.: Наука, 2005.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2008.

3. Письменный Д.Т. Конспект лекций по высшей математике, т. 1 – 2.– М: АЙРИС ПРЕСС, 2011.

4. Письменный Д.Т. Сборник задач по высшей математике, 2 курс. – М: АЙРИС ПРЕСС, 2007.

5. Письменный Д.Т. Сборник задач по высшей математике, 1 курс. – М: АЙРИС ПРЕСС, 2008.

6. Минорский В.П. Сборник задач по высшей математике. – М: ФМ, 2006.

7. Сазонов А.Л., Шифф В.К. Статистический анализ. – М: СПБГУТД, 2007.

8. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: ВШ, 2007.

Вопросы к экзамену.

1. Определение первообразной, свойства первообразной, определение неопределенного интеграла.

2. Свойства неопределенного интеграла, вытекающие из определения. Линейные свойства неопределенного интеграла.

3. Замена переменой в неопределенном интеграле. Простейшие замены.

4. Метод интегрирования по частям.

5. Площадь криволинейной трапеции. Определение определенного интеграла.

6. Свойства определенного интеграла, вытекающие из определения. Линейные свойства определенного интеграла.

7. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

8. Вычисление площадей фигур. Вычисление объемов тел при помощи определенного интеграла.

9. Дифференциальные уравнения первого порядка. Основные определения.

10. Дифференциальные уравнения первого порядка с разделенными переменными.

11. Однородные дифференциальные уравнения первого порядка.

12. Линейные дифференциальные уравнения первого порядка.

13. Дифференциальные уравнения второго порядка. Основные определения.

14. Линейные однородные дифференциальные уравнения второго порядка.

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

16. Линейные неоднородные дифференциальные уравнения второго порядка.

17. Ряды. Основные определения.Правила действия с рядами.

18. Признаки сходимости рядов с положительными членами.

19. Знакочередующиеся ряды. Теорема Лейбница.

20. Степенные ряды. Основные определения.

21. Теорема Абеля сходимости степенных рядов ( без доказательства).

22. Радиус сходимости, интервал и область сходимости степенного ряда.

23. Ряды Тейлора и МакЛорена.Основные определения теории вероятностей. Случайное событие. Классическая вероятность.

24. Алгебра событий. Совместные и несовместные события. Теоремы сложения вероятностей. Зависимые и независимые события. Теоремы умножения вероятностей. Вероятность хотя бы одного события.

25. Априорная и апостериорная вероятность (формула полной вероятности и формула Байеса).

МАТЕМАТИКА

Методические указания и контрольные задания 3 и 4

для студентов-заочников 1-го курса

Методические указания и контрольные задания 3 и 4 для студентов заочной сокращенной формы обучения РИНПО

по направлениям:

26200062 - Технология изделий легкой промышленности по профилю «Технология швейных изделий»

262200.62 - Конструирование изделий легкой промышленности по профилю «Конструирование швейных изделий»

100800.62 - Товароведение

Составители Г. П. Мещерякова Е.В. Наумова

Санкт-Петербург

УТВЕРЖДЕНО

на заседании методической комиссии

Регионального института непрерывного обучения

протокол № 1 от 14. 09. 2012

Рецензент

Н. В. Дробатун

Оригинал подготовлен составителями и издан в авторской редакции

Подписано в печать11.10.12. Формат 60х84 1/16.

Усл. печ. л. 1,7_. Тираж _100_. Заказ 281/12

Электронный адрес: http://alt-rinpo.sutd.ru/

Отпечатано в типографии СПГУТД.

191028, Санкт - Петербург, ул. Моховая, 26

При выполнении контрольной работы на титульном листе указывается:

фамилия, имя, отчество;

номер студенческого билета;

название дисциплины, номер контрольной работы, номер варианта.

Номер варианта соответствует последней цифре номера студенческого билета.

Перечень контрольных заданий по методичке кафедры математики

КОНТРОЛЬНАЯ РАБОТА N 3 (методичка к/р 3,4)

Нечетный год поступления N 1(1 -10), 2(1 – 10), 3(1 – 10), 4(1 – 10).

Четный год поступления N 1(11 -20), 2(11 – 20), 3(11 – 20), 4(11 – 20).

КОНТРОЛЬНАЯ РАБОТА N 4 (методичка к/р 3,4)

Нечетный год поступления N 1 (1 -10), 2 (1 - 10), 3 (1 - 10), 4 (1 - 10), 5(1 - 10).

Четный год поступления N 1 (11 -20), 2 (11 - 20), 3 (11 - 20), 4 (11 - 20), 5(11 - 20).

Контрольная работа № 3

Неопределенный интеграл

Определение и свойства неопределенного интеграла

Литература. [1], гл. Х, §1-3, упр. 2, 5, 7, 9, 11, 14, 16, 17, 25, 41, 46, 49, 58, 60, 66.