Предел и непрерывность функции
Практически предел функции находят не на основании определения предела функции, а на основании теорем о пределе функции.
Теорема. Если при 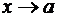 существуют пределы функций
существуют пределы функций 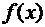 и
и 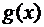 , то:
, то:
1. 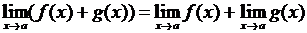 ;
;
2. 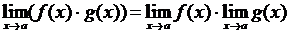 ;
;
3. 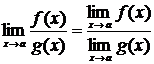 , где
, где 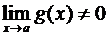 ;
;
4. 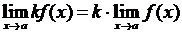 , где
, где 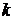 - постоянный множитель.
- постоянный множитель.
Пример 7.Вычислить 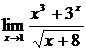 .
.
Решение. Так как
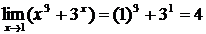 , а
, а 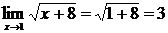 ,
,
то по теореме о пределе частного получаем, что 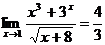 .
.
Но не всегда можно применять теоремы о пределах без предварительного преобразования функций, стоящих под знаком предела. При этом возможны следующие неопределенные ситуации: 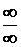 ,
, 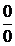 ,
, 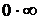 ,
, 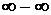 ,
, 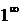 .
.
Приемом раскрытия неопределенности вида 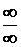 является деление числителя и знаменателя на наивысшую степень x.
является деление числителя и знаменателя на наивысшую степень x.
При неопределенности вида 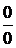 требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
Неопределенности же вида 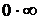 и
и 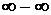 путем преобразований приводят к одному из рассмотренных случав
путем преобразований приводят к одному из рассмотренных случав 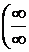 или
или 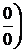 . Поясним сказанное на примерах.
. Поясним сказанное на примерах.
Пример 8. Вычислить 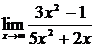 .
.
Решение. Наивысшая степень x вторая, делим числитель и знаменатель на 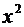 . Получим
. Получим
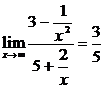 , так как
, так как 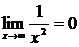 и
и 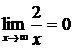 .
.
Пример 9. Вычислить 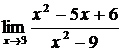 .
.
Решение. Имеет место неопределенность вида 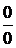 . Разложим числитель и знаменатель дроби на множители. Получим
. Разложим числитель и знаменатель дроби на множители. Получим
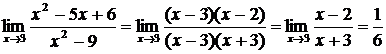 .
.
Пример 10. Вычислить 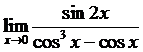 .
.
Решение. Числитель и знаменатель дроби при 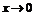 стремятся к нулю. Преобразуем функцию, выделим общий множитель
стремятся к нулю. Преобразуем функцию, выделим общий множитель
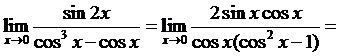
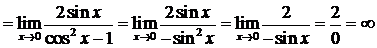 .
.
Пример 11. Вычислить 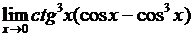 .
.
Решение. Так как 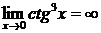 , а
, а 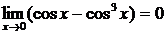 , то имеет место неопределенность вида
, то имеет место неопределенность вида 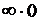 .
.
Выполним преобразования
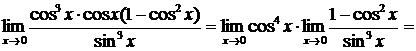
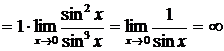 .
.
Пример 12. Найти точки разрыва функции.
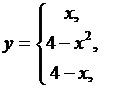 если
если 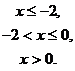
Решение. На интервалах 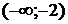 ,
, 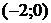 и
и 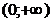 функция непрерывна. Проверке подлежат только точки
функция непрерывна. Проверке подлежат только точки 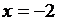 и
и 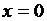 .
.
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке. Рассмотрим точку 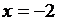 .
. 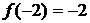 .
.
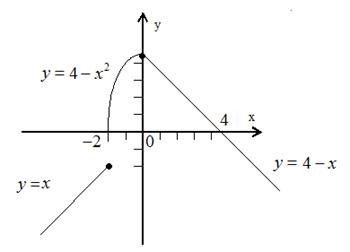
Рис. 4.
Вычислим односторонние пределы
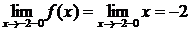 ,
, 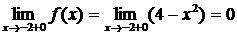 .
.
Так как односторонние пределы не совпадают, 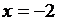 - точка разрыва функции.
- точка разрыва функции.
Рассмотрим точку 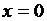 .
. 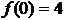 ,
,
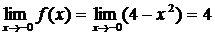 ,
, 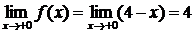 ,
,
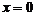 - точка непрерывности функции, выполнены все условия непрерывности.
- точка непрерывности функции, выполнены все условия непрерывности.
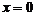 - точка непрерывности функции, выполнены все условия непрерывности (рис. 4).
- точка непрерывности функции, выполнены все условия непрерывности (рис. 4).
Производная
Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
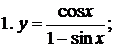
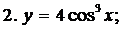
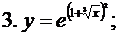 4.
4. 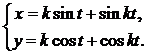
Решение.
1. 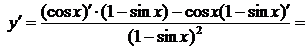
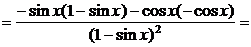
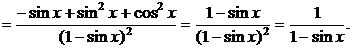
2. 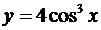 есть сложная функция.
есть сложная функция.
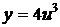 , где
, где 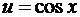 .
.
Производная сложной функции имеет вид
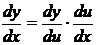 или
или 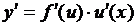 .
.
Следовательно,
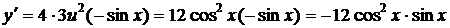 .
.
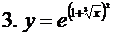 - сложная функция.
- сложная функция.
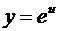 , где
, где 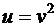 , а
, а 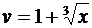 ,
,
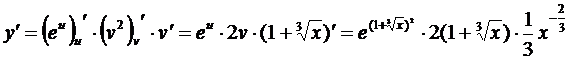 . 4.
. 4.
4. 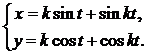
Функция 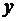 от независимой переменной
от независимой переменной 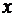 задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от 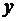 по
по 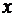 определяется формулой
определяется формулой
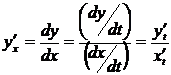 .
.
Находим производные от 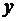 и
и 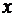 по параметру t:
по параметру t:
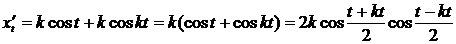 ,
, 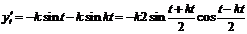 ,
,
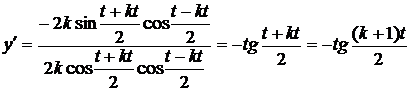 .
.
Пример 2. Составить уравнение касательной и нормали к кривой 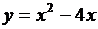 в точке, где
в точке, где 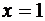 .
.
Решение. Уравнение касательной к кривой в точке 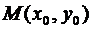
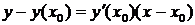 ,
,
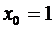 ,
, 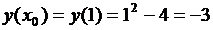 .
.
Для определения углового коэффициента касательной 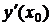 находим производную
находим производную
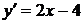 ,
,
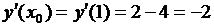 .
.
Подставляя значения 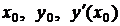 в уравнение, получим
в уравнение, получим
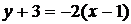 или
или 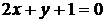 .
.
Уравнение нормали
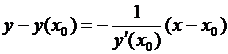 ,
,
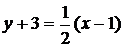 или
или 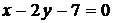 .
.
Пример 3. Точка совершает прямолинейное колебательное движение по закону 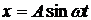 . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени 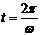 .
.
Решение. Найдем скорость 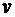 и ускорение а движения в любой момент времени t
и ускорение а движения в любой момент времени t
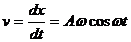 ;
; 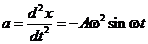 .
.
При 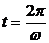
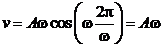 ,
, 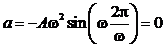 .
.
