Определители второго и третьего порядков.
МАТЕМАТИКА
Методические указания и контрольные задания 1 и 2 для студентов заочной формы обучения
Направления:
29.03.01 (262000.62) - Технология изделий легкой промышленности.
29.03.05 (262200.62) - Конструирование изделий легкой промышленности.
29.03.02 (261100.62) – Технология и проектирование текстильных изделий.
29.03.04 (261400.62) – Технология художественной обработки материалов.
29.03.06 (100700.62) – Торговое дело.
38.03.07 (100800.62) - Товароведение.
20.03.01 (280700.62) - Техносферная безопасность
| Мещерякова Г. П. Наумова Е. В. Мажара С. Ф. |
Санкт-Петербург
УТВЕРЖДЕНО
на заседании методического семинара
кафедры математики
протокол № от
Рецензент
Н. В. Дробатун
 |
Оригинал подготовлен составителями и издан в авторской редакции
Подписано в печать______ Формат 60х80 1/16.
Печать трафаретная. Усл. печ. л. 1,3_. Тираж _100_. Заказ ___
Электронный адрес: http://alt-rinpo.sutd.ru/ Отпечатано в типографии СПГУТД.
191028, Санкт - Петербург, ул. Моховая, 26
При выполнении контрольной работы на титульном листе указывается:
фамилия, имя, отчество;
номер студенческого билета;
название дисциплины, номер контрольной работы, номер варианта.
Номер варианта соответствует последней цифре номера студенческого билета. Например, номер кончается на 5, то для четного года поступления делаются 1.15, 2.15, 3.15, 4.15 задания, а при нечетном годе – 1.5, 2.5, 3.5, 4.5.
Перечень контрольных заданий по методичке кафедры математики
КОНТРОЛЬНАЯ РАБОТА N 1 (методичка к/р 1,2)
Нечетный год поступления N 1(1 -10), 2(1 – 10), 3(1 – 10), 4(1 – 10).
Четный год поступления N 1(11 -20), 2(11 – 20), 3(11 – 20), 4(11 – 20).
КОНТРОЛЬНАЯ РАБОТА N 2 (методичка к/р 1,2)
Нечетный год поступления N 1 (1 -10), 2 (1 - 10), 3 (1 - 10), 4 (1 - 10), 5(1-10).
Четный год поступления N 1 (11 -20), 2 (11 - 20), 3 (11 - 20), 4 (11 - 20), 5(11 - 20).
Контрольная работа № 1
Определители второго и третьего порядков.
Для матрицы A размером 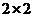 определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
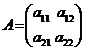 det(A) =
det(A) = 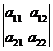 = a11 a22 – a12 a21.
= a11 a22 – a12 a21.
Для матрицы А размером 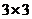 определитель находится по формуле
определитель находится по формуле
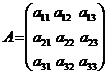 det(A) =
det(A) = 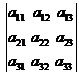 = a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
= a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
- a12 a21 a33 - a11a23 a32.
Системы координат
Пример. Найти расстояние между точками М1(1, -2, -3) и М2(-3, 1, 1). Определить координаты точки С, делящей отрезок М1М2 в отношении 2:3.
Решение.
Используя формулу
М1М2 = 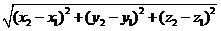
 ,
,
получим М1М2 = 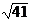 .
.
2. Координаты точки С определим по формуле вида
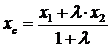 ,
,
где 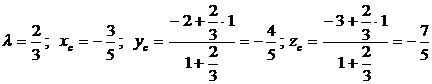 .
.
Векторная алгебра
Пример 1. Даны точки М1(1, -2, -3), М2(-3, 1, 1). Найти длину вектора 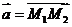 .
.
Решение.Вектор 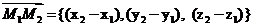 . Следовательно
. Следовательно 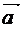 = {-3-1, 1+2, 1+3} ={-4, 3, 4}. Длина вектора находится по формуле ça ç=
= {-3-1, 1+2, 1+3} ={-4, 3, 4}. Длина вектора находится по формуле ça ç= 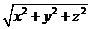 .
. 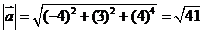
Пример 2.Найти угол φ между векторами 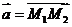 и
и 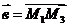 , если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
, если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
Решение. Для нахождения cosφ используем формулу
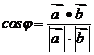
где 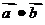 - скалярное произведение векторов
- скалярное произведение векторов 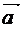 и
и 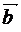 .
.
Определим координаты векторов 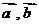 и cosφ:
и cosφ:
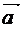 = (-3-1, 1+2, 1+3) =(-4, 3, 4),
= (-3-1, 1+2, 1+3) =(-4, 3, 4), 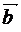 = (3-1, 2+2, 2+3) = (2, 4, 5),
= (3-1, 2+2, 2+3) = (2, 4, 5),
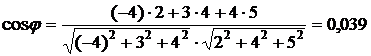 ,
,
φ = 87045'54".
Пример 3. Даны координаты вершин пирамиды А1(1, -2, -3), А2(-3, 1, 1), А3(4, 3, -1), А4(3, 2, 2). Найти площадь грани А1 А2 А3 и объем пирамиды.
Решение. Площадь треугольника А1А2А3 найдем, используя геометрический смысл векторного произведения векторов
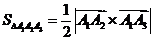 ,
,
где 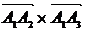 - векторное произведение векторов.
- векторное произведение векторов.
Вначале находим 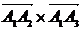
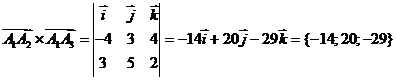 ,
,
а затем
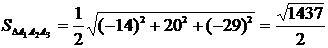 ед2.
ед2.
Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
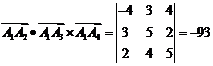 ,
,
следовательно, 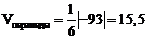 ед3.
ед3.
Уравнения линий на плоскости
Прямая на плоскости
Прямую на плоскости можно задать многими способами. При решении задач на прямую часто используются следующие типовые уравнения и соотношения:
1. Уравнения прямой с угловым коэффициентом 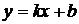 , где k – угловой коэффициент (
, где k – угловой коэффициент ( 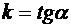 ,
, 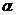 - угол наклона прямой к оси Ox), b – величина отрезка, отсекаемого прямой на оси Oy.
- угол наклона прямой к оси Ox), b – величина отрезка, отсекаемого прямой на оси Oy.
2. Уравнение прямой, проходящей через данную точку М(x0, y0) c данным угловым коэффициентом k
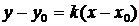 .
.
3. Уравнение прямой, проходящей через две данные точки M1(x1, y1) и M2(x2, y2)
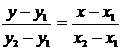 .
.
Заметим, что в случае 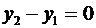 , уравнение принимает вид
, уравнение принимает вид 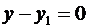 . Аналогично, если
. Аналогично, если 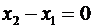 , уравнение прямой записывается
, уравнение прямой записывается 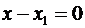 .
.
4. Расстояние d от точки М0 до прямой 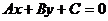 определяется по формуле
определяется по формуле
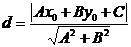 .
.
5. Угол j, отсчитываемый против часовой стрелки от прямой 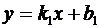 до прямой
до прямой 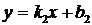 , определяется по формуле
, определяется по формуле
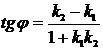 .
.
Из формулы следует:
1) прямые l1 и l2 параллельны, если 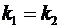 ;
;
2) прямые l1 и l2 перпендикулярны, если 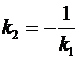 .
.
6. Уравнения биссектрис углов между прямыми 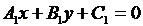 и
и 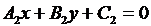 имеют вид
имеют вид
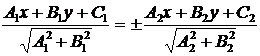 .
.
7. Точка пересечения медиан делит любую из них на части в отношении 2:1 (считая от вершины).
Пример. Даны вершины треугольника А(-3,-3), В(2,7) и С(5,1). Требуется написать уравнения сторон треугольника, определить угол А треугольника, найти уравнение медианы АК и высоты АМ.
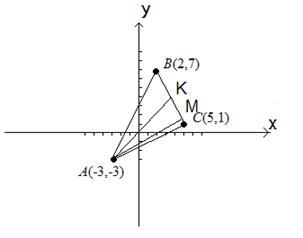
Рис. 1.
Решение. Чтобы написать уравнение стороны АВ треугольника, используем вид уравнения прямой, проходящей через две точки:
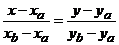
AВ: 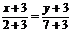 или у = 2х + 3.
или у = 2х + 3.
Аналогично
АС: 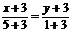 или у = 0,5х -1,5
или у = 0,5х -1,5
СВ: 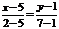 или у = -2х +11.
или у = -2х +11.
Тогда тангенс угла А определяется по формуле:
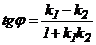 , k1=2, k2 = 0,5. Следовательно
, k1=2, k2 = 0,5. Следовательно 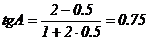
Ищем уравнение медианы АК. Для этого определяем координаты точки К, учитывая, что отрезок ВС в точке К делится пополам и, следовательно,
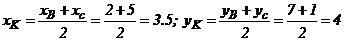
АК 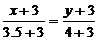 или
или 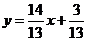
Ищем уравнение высоты АМ, опущенного из вершины А на сторону ВС :
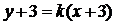 , где
, где 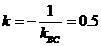 .
.
Следовательно, уравнение АМ: 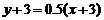 или у - 0,5х +1,5 =0
или у - 0,5х +1,5 =0
Линии второго порядка
Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С(x0, y0) (случай В).
А В
| Окружность | 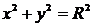 | 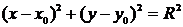 | |
| Эллипс | 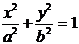 | 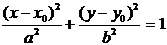 | |
| Гипербола | 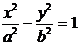 | 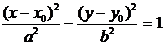 | |
| Парабола | 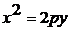 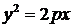 | 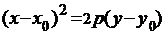 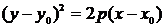 |
Пример 1. Пусть задано уравнение х2 + y2 - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра?
Приведем данное уравнение к виду 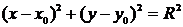 . Выделим полный квадрат относительно х, прибавляя и вычитая число 4
. Выделим полный квадрат относительно х, прибавляя и вычитая число 4
x2 + y2 - 4x = (x2 - 4x + 4) + y2 - 4 = 0 или (x - 2)2 + y2 = 22. х0 = 2, у0 = 0, R = 2.
Пример 2.Дано уравнение кривой второго порядка 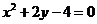 . Определить тип кривой, найти ее параметры и сделать чертеж.
. Определить тип кривой, найти ее параметры и сделать чертеж.
Решение.Сравнивая с табличными данными находим, что это парабола, вершига которой находится в точке С(x0, y0) . приводим уравнение параболы к виду 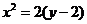 .
.
х0 = 0, у0 = 2, р = 1. Чертеж
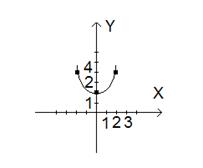
Рис. 2.
Контрольная работа 1. Задания.
1. Решить систему методами Крамера и последовательных исключений
| 1.1. | 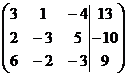 . . | 1.11. | 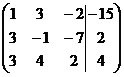 . . |
| 1.2 | 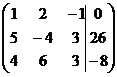 . . | 1.12. | 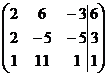 . . |
| 1.3. | 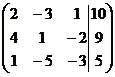 . . | 1.13. | 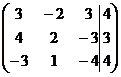 . . |
| 1.4. | 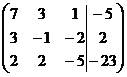 . . | 1.14. | 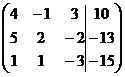 . . |
| 1.5. | 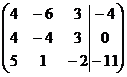 . . | 1.15. | 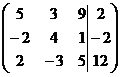 . . |
| 1.6. | 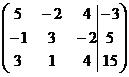 . . | 1.16. | 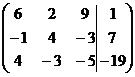 . . |
| 1.7. | 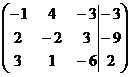 . . | 1.17. | 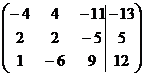 . . |
| 1.8. | 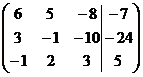 . . | 1.18. | 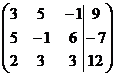 . . |
| 19. | 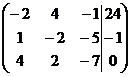 . . | 1.19. | 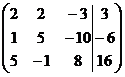 . . |
| 1.10. | 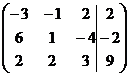 . . | 1.20. | 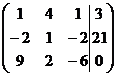 . . |
2. Даны координаты вершин пирамиды 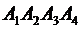 . Средствами векторной алгебры найти:
. Средствами векторной алгебры найти:
1) длину ребра 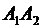 ;
;
2) угол между ребрами 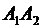 и
и 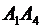 ;
;
3) уравнение плоскости 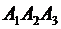 ;
;
4) уравнение перпендикуляра, опущенного из вершины 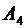 на грань
на грань 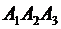 ;
;
5) площадь грани 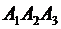 ;
;
6) объем пирамиды.
| 2.1. | 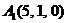 , , | 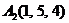 , , | 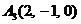 , , | 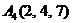 . . |
| 2.2. | 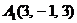 , , | 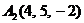 , , | 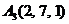 , , | 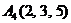 . . |
| 2.3. | 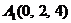 , , | 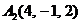 , , | 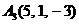 , , | 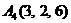 . . |
| 2.4. | 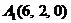 , , | 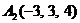 , , | 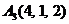 , , | 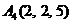 . . |
| 2.5. | 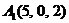 , , | 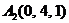 , , | 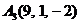 , , | 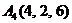 . . |
| 2.6. | 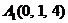 , , | 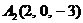 , , | 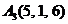 , , | 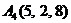 . . |
| 2.7. | 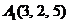 , , | 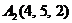 , , | 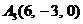 , , | 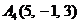 . . |
| 2.8. | 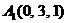 , , | 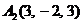 , , | 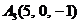 , , | 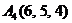 . . |
| 2.9. | 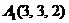 , , | 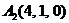 , , | 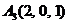 , , | 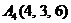 . . |
| 2.10. | 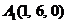 , , | 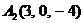 , , | 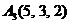 , , | 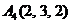 . . |
| 2.11. | 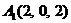 , , | 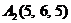 , , | 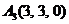 , , | 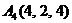 . . |
| 2.12. | 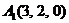 , , | 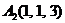 , , | 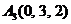 , , | 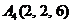 . . |
| 2.13. | 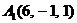 , , | 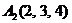 , , | 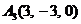 , , | 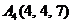 . . |
| 2.14. | 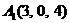 , , | 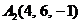 , , | 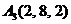 , , | 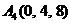 . . |
| 2.15. | 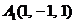 , , | 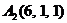 , , | 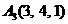 , , | 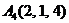 . . |
| 2.16. | 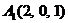 , , | 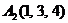 , , | 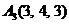 , , | 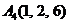 . . |
| 2.17. | 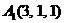 , , | 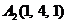 , , | 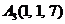 , , | 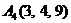 . . |
| 2.18. | 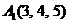 , , | 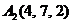 , , | 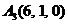 , , | 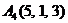 . . |
| 2.19. | 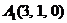 , , | 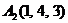 , , | 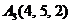 , , | 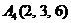 . . |
| 2.20. | 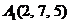 , , | 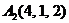 , , | 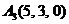 , , | 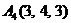 . . |
В задачах 3.1 – 3.20 по аналитической геометрии сделать чертеж.
3. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж
| № | А | В | С | № | А | В | С |
| 3.1. | (-5, 3) | (1,6) | (5, 1) | 3.11 | (1, 5) | (4, 0) | (-5,-4) |
| 3.2. | (-7, 1) | (5, 0) | (2, 5) | 3.12 | (4, 2) | (2, 0) | (-1, 2) |
| 3.3. | (5, 1) | (0, 4) | (-2, 2) | 3.13 | (0, -2) | (-2, 1) | (3, 4) |
| 3.4. | (5, 2) | (-1, 0) | (3, 4) | 3.14 | (-1, 2) | (1, 1) | (-5, 3) |
| 3.5. | (2, -2) | (3, -4) | (2, -1) | 3.15 | (4, 2) | (-3, 3) | (2, -1) |
| 3.6. | (1, 0) | (2, 5) | (-1, 1) | 3.16 | (4, 4) | (5, 1) | (-1, 0) |
| 3.7. | (0, -3) | 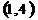 | (-2, -1) | 3.17 | (-2, 4) | (5, 1) | (0, -3) |
| 3.8. | (-2, 1) | (3, 1) | (0, -2) | 3.18 | 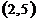 | (-1, 1) | (0,3) |
| 3.9. | (-3, 3) | (7, 5) | (4, 1) | 3.19 | (1, 5) | (-5, 3) | (1,3) |
| 3.10 | (2, 0) | (5, -2) | (8, 2) | 3.20 | 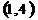 | (-2,1) | (0, -3) |
4. Указать тип кривой второго порядка, найти ее параметры и сделать чертеж.
4.1. 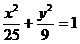 . . | 4.11. 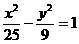 |
4.2. 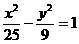 | 4.12. 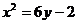 |
4.3. 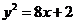 | 4.13. 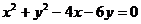 |
4.4. 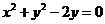 | 4.14. 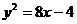 |
4.5. 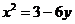 | 4.15. 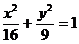 |
4.6. 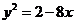 | 4.16. 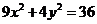 |
4.7. 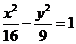 | 4.17. 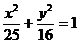 |
4.8. 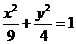 | 4.18. 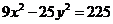 |
4.9. 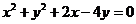 | 4.19. 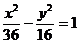 |
4.10. 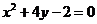 | 4.20. 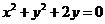 |
Контрольная работа №2
Производная
Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
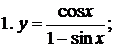
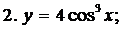
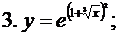 4.
4. 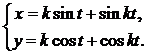
Решение.
1. 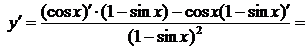
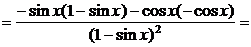
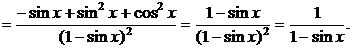
2. 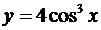 есть сложная функция.
есть сложная функция.
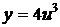 , где
, где 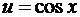 .
.
Производная сложной функции имеет вид
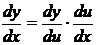 или
или 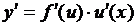 .
.
Следовательно,
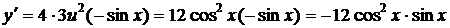 .
.
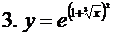 - сложная функция.
- сложная функция.
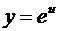 , где
, где 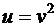 , а
, а 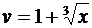 ,
,
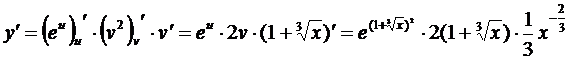 . 4.
. 4.
4. 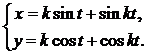
Функция 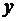 от независимой переменной
от независимой переменной 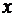 задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от 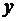 по
по 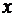 определяется формулой
определяется формулой
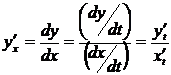 .
.
Находим производные от 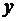 и
и 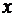 по параметру t:
по параметру t:
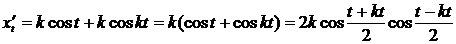 ,
, 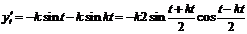 ,
,
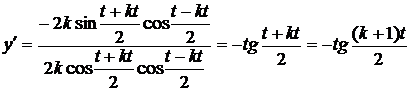 .
.
Пример 2. Составить уравнение касательной и нормали к кривой 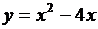 в точке, где
в точке, где 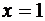 .
.
Решение. Уравнение касательной к кривой в точке 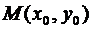
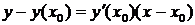 ,
,
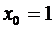 ,
, 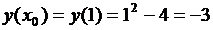 .
.
Для определения углового коэффициента касательной 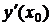 находим производную
находим производную
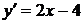 ,
,
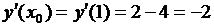 .
.
Подставляя значения 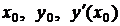 в уравнение, получим
в уравнение, получим
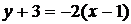 или
или 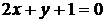 .
.
Уравнение нормали
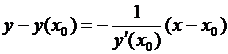 ,
,
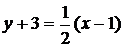 или
или 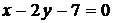 .
.
Пример 3. Точка совершает прямолинейное колебательное движение по закону 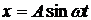 . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени 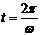 .
.
Решение. Найдем скорость 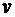 и ускорение а движения в любой момент времени t
и ускорение а движения в любой момент времени t
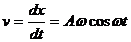 ;
; 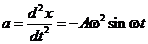 .
.
При 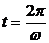
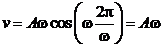 ,
, 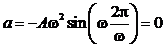 .
.
Рис. 5.
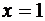 есть точка максимума,
есть точка максимума, 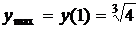 .
.
6. Исследуем график функции на выпуклость и вогнутость
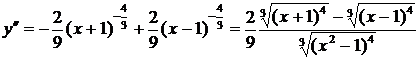 .
.
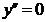 в точке
в точке 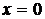 ;
; 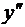 не существует в точках
не существует в точках 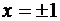 . Эти точки могут быть абциссами точек перегиба.
. Эти точки могут быть абциссами точек перегиба.
Исследуем знак второй производной на интервале [0; ∞) (рис.6)









 0 1
0 1
Рис. 6
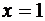 не является точкой перегиба.
не является точкой перегиба.
Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0) (рис.7)
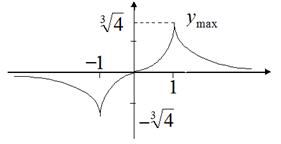
Рис. 7
Пример 2. Найти наибольшее и наименьшее значения функции
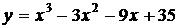 на отрезке [-4; 4].
на отрезке [-4; 4].
Решение. 1. Найдем критические точки функции 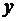 , лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:
, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках: 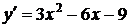 ;
; 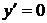 в точках
в точках 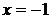 и
и 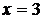 . Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:
. Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках: 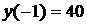 и
и 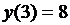 .
.
2. Вычислим значения функции на концах отрезка [-4; 4]: 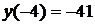 и
и 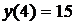 .
.
3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции 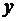 на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке
на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке 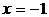 , а ее наименьшее значение равно -41 и достигается на левой границе отрезка
, а ее наименьшее значение равно -41 и достигается на левой границе отрезка 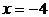 .
.
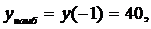
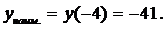
Функции нескольких переменных
Литература. [1], гл.VШ, § 1 - 4.
1. Частные производные.
Литература. [1], гл. VIII, § 5, 6, упр. 1-10.
Пример. 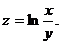
1. Найти область определения функции.
2. Проверить, что 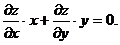
3. Проверить, что 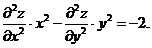
Решение.
1. Под знаком логарифма может стоять только положительное выражение, следовательно
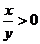
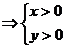 или
или 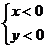 .
.
Сделаем чертеж
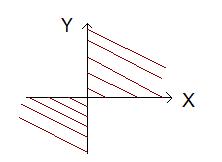
Рис. 3.
2. При вычислении частной производной по 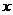 рассматриваем функцию
рассматриваем функцию 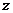 как функцию только от переменной
как функцию только от переменной 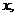 а при дифференцировании по
а при дифференцировании по 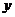 - как функцию только от
- как функцию только от 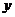 :
:
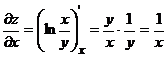 ,
,
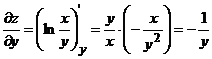 ,
,
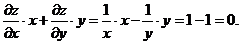
3. При вычислении второй производной по 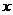 также рассматриваем функцию
также рассматриваем функцию 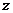 как функцию только от переменной
как функцию только от переменной 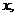 а при дифференцировании по
а при дифференцировании по 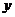 - как функцию только от
- как функцию только от 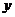 :
:
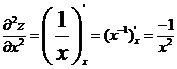 ,
,
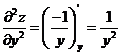 ,
,
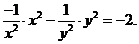
Контрольная работа 2. Задания
1. Найти точки разрыва функции, если они существуют. Сделать чертеж функции.
1.1. 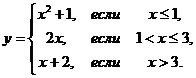 | 1.11. 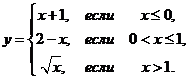 |
1.2. 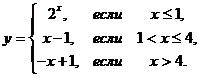 | 1.12. 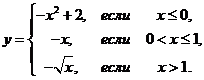 |
1.3. 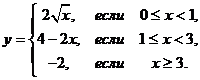 | 1.13. 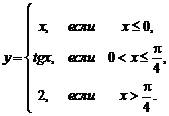 |
1.4. 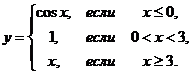 | 1.14. 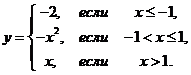 |
1.5.  | 1.15. 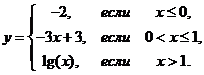 |
1.6.  | 1.16. 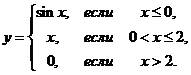 |
1.7. 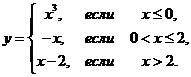 | 1.17.  |
1.8. 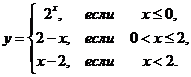 | 1.18. 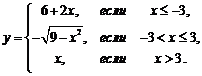 |
1.9. 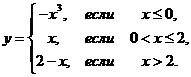 | 1.19. 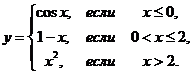 |
1.10. 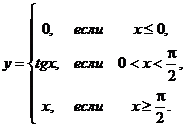 | 1.20. 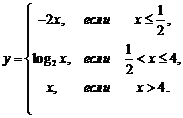 |
2. Найти производные 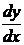 данных функций.
данных функций.
| № | а | б | в | г |
| 2.1 | 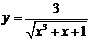 | 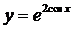 | 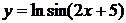 | 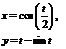 |
| 2.2 | 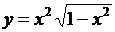 | 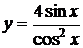 | 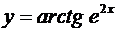 | 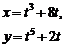 |
| 2.3 | 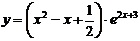 | 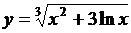 | 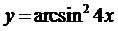 | 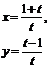 |
| 2.4 |  | 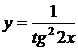 | 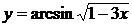 | 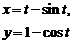 |
| 2.5 | 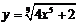 | 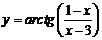 | 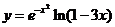 | 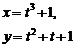 |
| 2.6 | 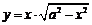 | 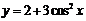 | 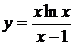 | 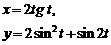 |
| 2.7 | 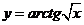 | 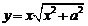 | 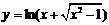 | 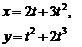 |
| 2.8 | 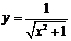 | 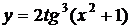 | 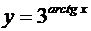 | 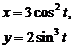 |
| 2.9 |  | 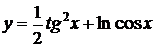 | 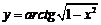 | 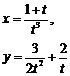 |
| 2.10 | 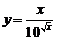 | 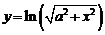 | 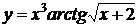 | 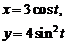 |
| 2.11 | 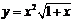 | 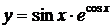 | 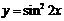 | 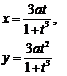 |
| 2.12 | 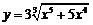 | 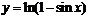 | 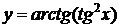 | 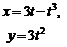 |
| 2.13 | 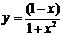 | 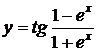 | 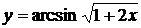 | 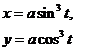 |
| 2.14 | 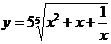 | 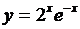 | 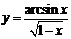 | 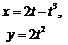 |
| 2.15 | 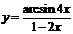 | 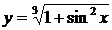 | 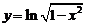 | 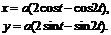 |
| 2.16 | 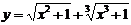 | 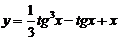 | 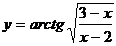 | 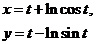 |
| 2.17 | 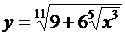 | 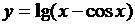 | 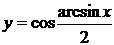 | 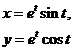 |
| 2.18 | 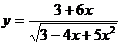 | 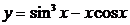 | 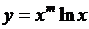 | 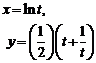 |
| 2.19 | 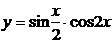 | 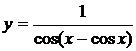 | 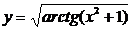 | 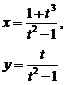 |
| 2.20 | 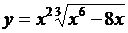 | 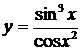 | 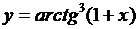 |
