Производная функции и её приложения
Приращение функции
Определение 1.Приращением величины называется разность между новым значением величины и старыми обозначается буквойΔ.
ΔN = N2 – N1.
Другими словами, приращение величины показывает на сколько изменилась величина.
Определение 2. Приращением аргумента (функции) называется разность между новым значением аргумента (функции) и старым и обозначается буквой Δ.
Δх = х2 – х1 - приращение аргумента;
Δу = у2 – у1 - приращение функции.
Если известны начальное значение величины N и ее ΔN, то можно найти ее новое (наращенное) значение N2 = N + ΔN.
Примеры
1. Найти приращение функции у=2х2 – 1, если х изменился от 3 ед. до 3,5 ед.
Решение
Найдем значение функции у1 при х1=3: у1=2∙32 – 1=17 ед,
затем найдем у2 при х2 = 3,5: у2 = 2∙3,52 – 1 = 23,5 ед.
Тогда Δу = у2 – у1 = 23,5 – 17 = 6,5 ед.
Производная функции
ОпределениеПроизводной функции называется предел отношения приращения функции Δy к приращению аргумента Δx, когда приращение аргумента стремится к нулю, и обозначается 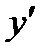 .
.
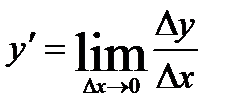 |
Производная производной первого порядка называется производной второго порядка.
y’’=(y’)’
Формулы дифференцирования
1. (С)′ = 0 11. (sin x)′ = cos x
2. (х)′ = 1 12. (cos x)′ = - sin x
3. (u + v – w)′ = u′ + v′ - w′ 13. (tg x)′ = 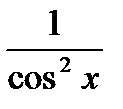
4. (u∙v)′ = uv′ +vu′ 14. (ctg x)′ = 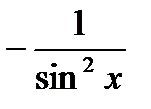
5. (Cx) = C 15. (ln x)′ = 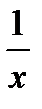
6. (Cu)′ = C(u)′ 16. (lg x)′ = 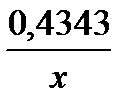
7. (x m)′ = m∙x m – 1 17. (a x)′ = a x∙ln x
8. 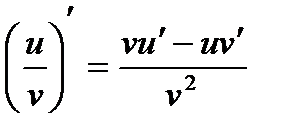 18. (e x)′ = e x
18. (e x)′ = e x
9. 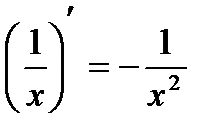 19. (arcsin x)′ =
19. (arcsin x)′ = 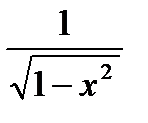
10. ( 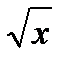 )′ =
)′ = 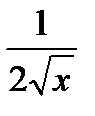 20. (arctg x)′ =
20. (arctg x)′ = 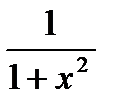
Замечание.Нахождение производной функции называется дифференцированием функции.
Примеры
Продифференцировать функции:
1. у = 2х3 – 4х2 + 5х – 3
Решение.По правилу (3) имеем:
у′ =(2х3)′ - (4х2)′ + (5х)′ – (3)′
Применяя к первым трем слагаемым правило (6), а к последнему – правило (1), получим:
у′ =2(х3)′ - 4(х2)′ + 5(х)′ – 0.
По правилу (5) и (2) имеем:
у′ =2∙3х2 - 4∙2х + 5 ∙1 = 6х2 - 8х + 5.
2. у = (х2 + 1)(2х + 3)
Решение.По правилу (4) имеем:
у′ = ((х2 + 1)(2х + 3))′ = (х2 + 1)(2х + 3)′ + (х2 + 1)′ (2х + 3)
По правилу (3) имеем:
у′ =(х2 + 1)((2х)′ + (3)′) + ((х2)′ + (1)′) (2х + 3)
По правилам (6), (2), (1) и (7)
у′ =(х2 + 1)(2 + 0) + (2х + 0)(2х + 3) =2х2 + 2 + 4х2 + 6х = 6х2 +6х + 2.
3. 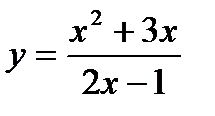
Решение. По правилу (8) имеем:
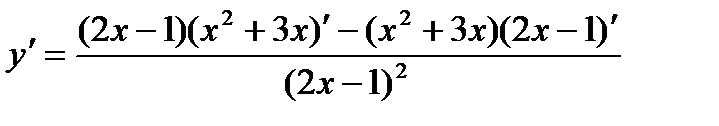
По правилам (7), (5), (1):
= 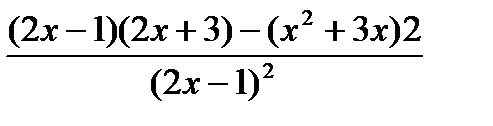
раскроем скобки и приведем подобные: 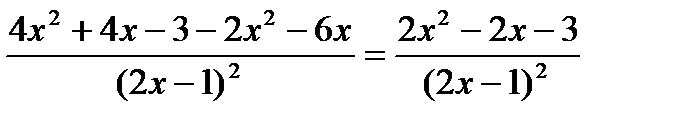 .
.
4. 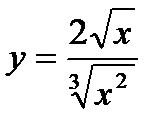
Решение.Упростим функцию:
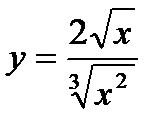 =
= 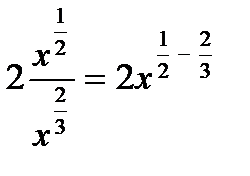 =
= 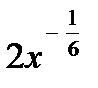
по правилу дифференцирования степенной функции (8) получим
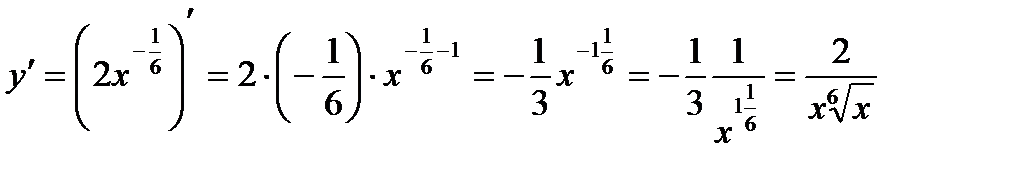
5. 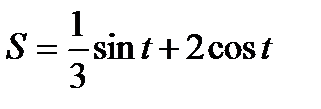
Решение.По правилу (8) имеем:
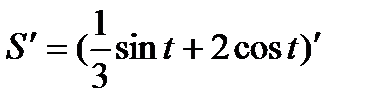 =
= 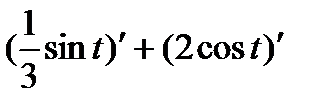 =
=
По правилу (6), (11), (12) имеем:
= 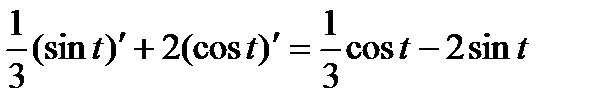
Практическая работа 1
"Дифференцирование функций и построение графиков"
Цель работы: формировать умения по выполнению дифференцирования функций и применению ее к решению задач
Основные понятия
Определение 1.Функция называется простой, если над аргументом выполняется одно функциональное действие.
Определение 2. Функция называется сложной, если над аргументом выполняется более одного функционального действия.
Замечание.Путем замены переменной сложную функцию можно свести к простой, но уже относительно новой переменной.
Например
Простая функция Сложная функция Замена Простая функция
y = x5 y =(3x – 2)5 u = 3x – 2 y = u5
y = sin x y = sin 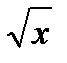 u =
u = 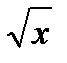 y = sin u
y = sin u
y = ln x y = ln cosx u = cosx y = ln u
y = 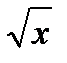 y =
y = 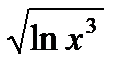 u = ln x3 y =
u = ln x3 y = 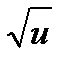
y = f(x) y = f(φ(x)) u = φ(x) y = f(u)
Производная сложной функции
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу (замене) на производную промежуточного аргумента (замены) по основному.
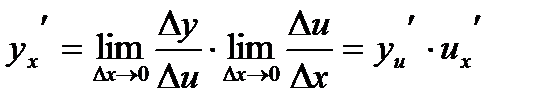 |
(1)
Например. Найти производную функции y = (3x2 – 5)3.
Решение. y’ = ((3x2 – 5)3) ’ Функция сложная.
Заменой переменной обозначимu = (3x2 – 5).
Тогда функция примет вид y = u3.
По (1) ищем ее производную в таком виде: y’ = (u3) ’=3u2∙u’.
Вернемся к старой переменной: y’ = (u3) ’=3u2∙u’ = 3(3x2 – 5)2(3x2 – 5)’
Взяв производную скобки, окончательно получим:
y’ = 3(3x2 – 5)2∙6х = 18х(3x2 – 5)2.
Замечание.
1) Для введения промежуточной переменной u необходимо помнить, что функция должна стать простой, т.е. иметь одно действие. Для этого необходимо разобраться в порядке действий в данной функции, найти последнее и оставить его, т.е. обозначить за u все, что есть, до последнего действия.
2)За u не обозначается постоянное число, помнить, что u – это функция.
3) За u не обозначается все выражение, т.к. тогда не будет ни одного действия.
Например.
1) y = 2(x – 1)5, u = (x – 1)  у = 2u5
у = 2u5
2) y = 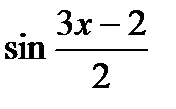 , u =
, u = 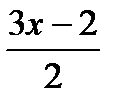
 y = sin u
y = sin u
3) 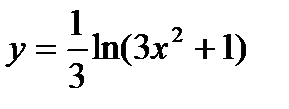 , u =
, u = 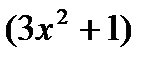
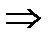 y =
y = 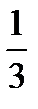 ln u
ln u
Примеры
Продифференцировать функции
1) y = (x3 – 4x + 1)3
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = (x3 – 4x + 1), сводящую данную функцию к простой y = u3.
И тогда, по формуле степенной функции (7) получим:
y’ =(u3)’=3u2∙u’ = 3 (x3 – 4x + 1)2(x3 – 4x + 1)’ =3 (x3 – 4x + 1)2(3х2 – 4)
2) 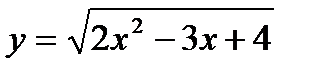
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = 2x2 – 3x + 4,сводящую данную функцию к простой: 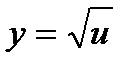 .
.
Тогда, по формуле (10):
( 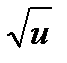 )′ =
)′ = 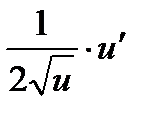 , получим:
, получим:
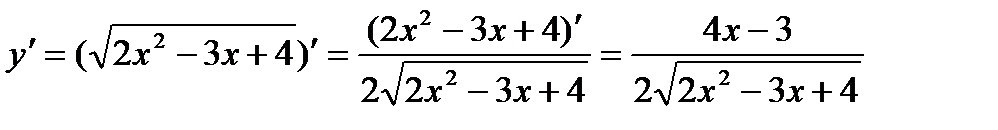
3) 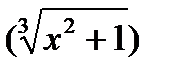
Если дан корень другой степени, то его нужно преобразовать в степень с дробным показателем и затем применить формулу (7).
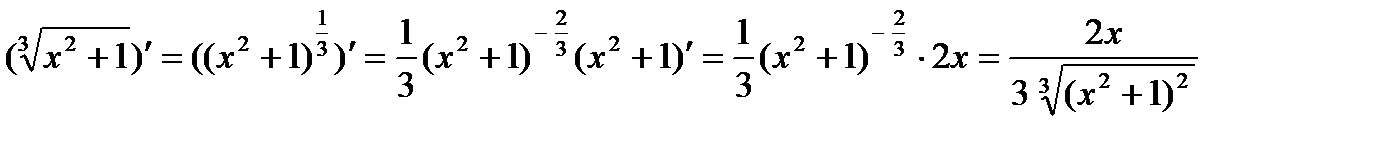
4) 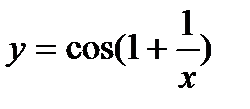
Решение
Функция сложная, введем промежуточную переменную 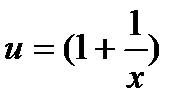 .
.
И по формуле (12):
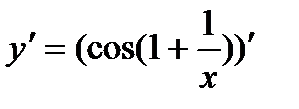
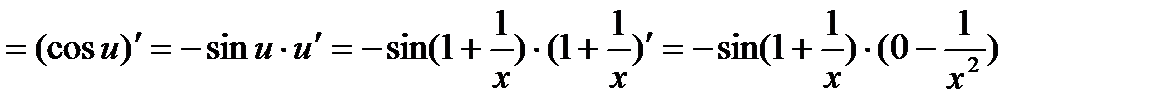 =
=
=