Понятие фундаментальной последовательности.

Понятие фундаментальной последовательности.

Последовательность { 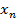} называется фундаментальной, если для любого ε>0 найдется номер N(ε) такой, что при n≥ N(ε) и для любого натурального ряда p(p=1,2,3…) выполняется неравенство 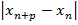<ε

Теорема24(о сходимости ограниченной последовательности с совпадающими нижним и верхним пределами.)

Для того, чтобы последовательность { 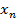} была сходящейся, необходимо и достаточно, чтобы она была ограничена и чтобы ее верхний 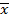и нижний 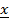пределы совпадали(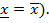

Док-во. Необходимость-считается, что последовательность { 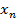} является сходящейся. Надо доказать, что она ограничена или 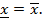в соответствии со свойством(теорема8) сходящаяся последовательность ограничена. А в соответствии с леммой5 сходящаяся последовательность имеет лишь одну предельную точку, совпадающую с пределом последовательности, т.е. 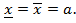Достаточность-считается, что последовательность { 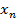} ограничена и 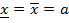. Надо доказать, что { 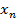} сходится. Выберем произвольное ε>0, и воспользуемся следствием1 из теоремы23. В соответствии с этим следствием интервал интервал ( 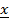- ε, 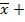ε) содержит все элементы последовательности, начиная с некоторого номера, т.е. этот интервал содержит бесконечно много элементов последовательности { 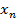}. Т.к. 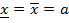, то этот интервал запишем в виде: (a- ε, 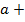ε). Этот интервал есть ε-окрестность точки a. он содержит бесконечно много элементов последовательности { 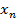}. Тогда в соответствии с 1-м определением предельной точки, число а является предельной точкой этой последовательности. Т.к. 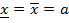то последовательность { 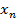}. Является сходящейся.

Критерий Коши сходимости числовой последовательности(теорема25).

Для того, чтобы последовательность { 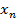} сходилась, необходимо и достаточно, чтобы она была фундаментальна.

Необходимость-считается, что последовательность { 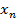} сходится. Надо доказать, что она является фундаментальной. По определению сход. последовательности для любого ε найдется N(ε) такой, что 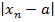< ε, n≥ N(ε). Номера n+p>n, поэтому при n≥ N(ε) выполняется неравенство 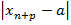<ε оценим 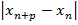. 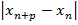= 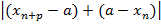≤ 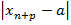+ 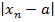<2ε. 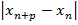< ε при n≥ N(ε).

Достаточность-считается, что последовательность фундаментальная, надо доказать, что она сходится. Воспользуемся теоремой 24. Надо доказать, что фундаментальная последовательность ограничена и 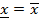. Ограниченность последовательности очевидна, т.к. выполняется 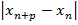< ε, при n≥ N(ε) и любом p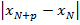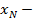. < ε -> ε< 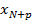< 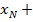ε. A=max {x1, x2, …x_n-1, x_n+ε}, тогда для всех n выполняется 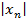<A. В соответствии с ним интервал ( 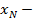ε, 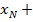ε) содержит в себе интервал ( 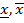) т.е. выполняется неравенство 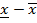≤ 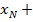ε-( 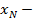ε)=2ε. 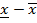<2ε, => 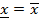, тогда по теореме24 фундаментальная последовательность является сходящейся.

Понятие производной функции, ее геометрический смысл.

Производной функции y’(x), f’(x) называетсяпредельное значение приращения функции к приращению аргумента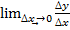

Геометрический смысл-tg угла наклона касательной к графику функции.

Правая и левая производные.

Правой(левой) производной функции y=f(x) называется правое(левое) предельное значение отношения приращения функции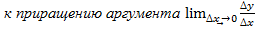

F’(x+0) правая производная, F’(x-0) левая производная.

Дифференциал функции.

Дифференциалом функции dy в точке x₀ называется главное приращение функции в этой точке dy=y’(x)*dx

Формула Лейбница.

Y=u(x)*v(x). (uv)⁽ⁿ⁾=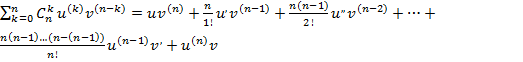

Дифференциал высшего порядка. Пусть функция y=f(x) дифференцируема в точке x. dy=f’(x)dx. Если функция f’(x) дифференцируема, то можно записать d(dy)=d²y=d(f’(x)dx)=d(f’(x)dx=f’’(x)dxdx=f’’(x)(dx)²

Если функция n-раз дифференцируема, то можно записать dⁿy=f⁽ⁿ⁾(x)(dx)ⁿ=f⁽ⁿ⁾(x)=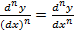

Дифференцирование функции, заданной параметрически. ,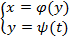

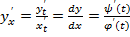
Правило Лопиталя(теорема30).Пусть функция f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀, пусть кроме того, 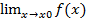= =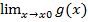0, 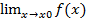= =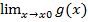∞ и производная g’(x) отлична от 0 в рассматриваемой окрестности. Тогда если существует предельное значение 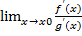, то существует и предельное значение 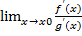и справедливо равенство: 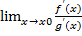= 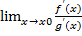. Замечание-если условие теоремы выполняется для f’(x) и g’(x), то справедливо 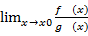=…… 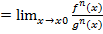. Данное правило используется для раскрытия неопределенностей вида , , .

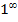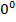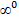Формула Тейлора(теорема31).

Пусть функция у=f(x) дифференцируема n-раз в точке x₀ и некоторой окрестности этой точки. Тогда для любой точки x из этой окрестности справедлива формула:

f(x)=f(x0)+ 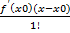+ +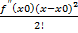…+ + 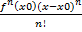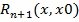, остаточное слагаемое.

В форме Пеана o((x-x0)’), в форме Лагранжа * .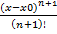

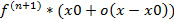Частный вид формулы Тейлора при x0 носит название формулы Маклорена.

Теорема 34.

Пусть функция y=f(x)имеет локальный экстремум в точке и дифференцируема в этой точке. Тогда f’( )=0.

Док-во: так как точка локального экстремума не является ни точкой возрастания ни точкой убывания функции, значит не выполняется равенство f’( )>0,f’( )<0,то очевидно, что f’( )=0.

Теорема 35(Ролля).

Пусть функция y=f(x) непрерывна на сегменте 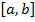и дифференцируема в любой внутренней точке этого сегмента. Пусть кроме того f(a)=f(b).Тогда внутри 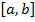найдется точка d , такая, что f’(d)=0.

Док-во: так как функция непрерывна на сегменте 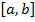,то она достигает на этом сегменте своих наибольшего M и наименьшего m значения. Могут реализоваться 2 случая:

a)значения m и M достигается на краях сегмента. Тогда из условия f(a)=f(b)следует, что M=m,но такое возможно только при f(x)=const.значит найдется точка d такая,что f’(d)=0.

Б)одно из значений m или M достигается на краю отрезка а другое внутри него в некоторой точке d,значит d-точка экстремума и f’(d)=0.

Теорема 36(Логранжа).

Пусть функция f(x) непрерывна на 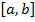и дифференцируема в любой точке внутри сегмента:f(b)-f(a)=f’(d)(b-a)-формула Логранжа. d- точка внутри .

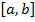Док-во: Построим вспомогательную функцию F(x)=f(x)-f(a)- 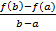(b-a).Эта функция удовлетворяет условиям теоремы Ролля. Действительно, функция непрерывна на 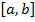.F(a)= 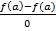- 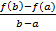(a-a)=0;F(b)=f(b)-f(a)- 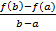(b-a)=0 таким образом F(a)=F(b) Вычислим F'(x):по теореме Ролля найдется точка d такая, что F’(d)=0=f’(d)= 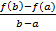àf(b)-f(a)=(b-a)f’(d).

Теорема 42

Пусть функция y=f(x) дважды дифференцируема в т. x₀ и пусть т. М (x₀,y₀) является точной точкой перегиба графика функции. Тогда y``(x₀)=0

Теорема 43

(1 условие) пусть функция y=f(x) дважды дифференцируема в некоторой окрестности т. x₀ и пусть f``(x₀)=0, тогда есди вторая производная функции f(x) слева и справа от точки x₀ в пределах выбранной окрестности имеет различный знак, то график функции в т. М (x₀,y₀) имеет перегиб.

Теорема 44

Пусть функция y=f(x) – трижды дифференцируема в т. x₀ , и пусть выполняется f``(x<sub>0</sub>)=0, f``(x₀)≠0. Тогда график функции f(x) в т. М (x₀,y₀) имеет перегиб.

Теорема 45

Пусть функция y=f(x) – n-раз дифференцируема в окрестности т. x₀ и (n+1) раз дифференцируема в самой т. x₀ .Пусть кроме того выполняется

f``(x₀)= f```(x₀)=… f⁽ⁿ⁾(x₀)=0, f⁽ⁿ⁺¹⁾(x₀)≠0 , тогда 1) если число n-четное, то график функции f(x) в т. М (x₀,y₀) имеет перегиб.2) если n-нечетное число и кроме того f`(x₀)=0, f⁽ⁿ⁺¹⁾(x₀)<0 (f⁽ⁿ⁺¹⁾(x₀)>0) , то фунуция f(x) в т. x₀ имеет локальный максимум ( ЛОКАЛЬНЫЙ МИНИМУМ)

Понятие фундаментальной последовательности.

Последовательность { 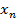} называется фундаментальной, если для любого ε>0 найдется номер N(ε) такой, что при n≥ N(ε) и для любого натурального ряда p(p=1,2,3…) выполняется неравенство 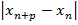<ε

Теорема24(о сходимости ограниченной последовательности с совпадающими нижним и верхним пределами.)

Для того, чтобы последовательность { 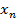} была сходящейся, необходимо и достаточно, чтобы она была ограничена и чтобы ее верхний 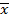и нижний 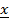пределы совпадали(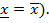

Док-во. Необходимость-считается, что последовательность { 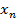} является сходящейся. Надо доказать, что она ограничена или 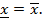в соответствии со свойством(теорема8) сходящаяся последовательность ограничена. А в соответствии с леммой5 сходящаяся последовательность имеет лишь одну предельную точку, совпадающую с пределом последовательности, т.е. 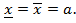Достаточность-считается, что последовательность { 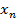} ограничена и 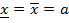. Надо доказать, что { 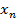} сходится. Выберем произвольное ε>0, и воспользуемся следствием1 из теоремы23. В соответствии с этим следствием интервал интервал ( 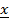- ε, 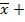ε) содержит все элементы последовательности, начиная с некоторого номера, т.е. этот интервал содержит бесконечно много элементов последовательности { 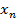}. Т.к. 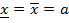, то этот интервал запишем в виде: (a- ε, 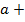ε). Этот интервал есть ε-окрестность точки a. он содержит бесконечно много элементов последовательности { 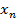}. Тогда в соответствии с 1-м определением предельной точки, число а является предельной точкой этой последовательности. Т.к. 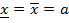то последовательность { 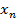}. Является сходящейся.

Критерий Коши сходимости числовой последовательности(теорема25).

Для того, чтобы последовательность { 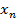} сходилась, необходимо и достаточно, чтобы она была фундаментальна.

Необходимость-считается, что последовательность { 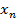} сходится. Надо доказать, что она является фундаментальной. По определению сход. последовательности для любого ε найдется N(ε) такой, что 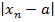< ε, n≥ N(ε). Номера n+p>n, поэтому при n≥ N(ε) выполняется неравенство 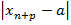<ε оценим 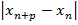. 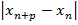= 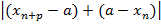≤ 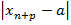+ 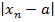<2ε. 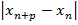< ε при n≥ N(ε).

Достаточность-считается, что последовательность фундаментальная, надо доказать, что она сходится. Воспользуемся теоремой 24. Надо доказать, что фундаментальная последовательность ограничена и 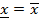. Ограниченность последовательности очевидна, т.к. выполняется 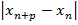< ε, при n≥ N(ε) и любом p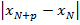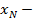. < ε -> ε< 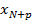< 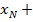ε. A=max {x1, x2, …x_n-1, x_n+ε}, тогда для всех n выполняется 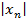<A. В соответствии с ним интервал ( 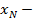ε, 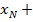ε) содержит в себе интервал ( 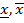) т.е. выполняется неравенство 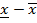≤ 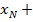ε-( 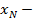ε)=2ε. 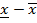<2ε, => 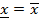, тогда по теореме24 фундаментальная последовательность является сходящейся.