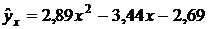Построение квадратичной регрессионной модели по методу наименьших квадратов

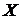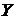Предположим, что СВ и связаны следующим уравнением 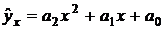. Система линейных уравнений относительно неизвестных параметров для нахождения оценок коэффициентов аппроксимирующего многочлена, полученная методом наименьших квадратов, имеет вид:

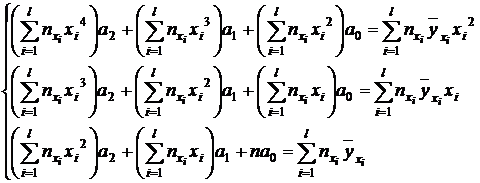(22)

Найденные из этой системы выборочные параметры 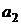, , 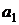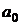подставляют в выборочное уравнение регрессии 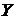на 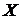: 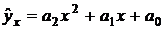и в итоге получают искомое уравнение регрессии.

Составим расчетную таблицу

№
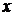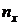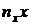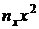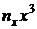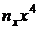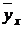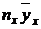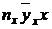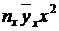	4,055 4,525 4,995 5,465 5,935 6,405 6,875 7,345 7,815 8,285		12,165 31,675 64,935 76,51 89,025 115,29 82,5 80,795 15,63 41,425	49,329 143,329 324,350 418,127 528,363 738,433 567,187 593,439 122,148 343,206	200,029 648,565 1620,129 2285,064 3135,836 4729,659 3899,414 4358,811 954,590 2843,464	811,119 2934,76 8092,55 12487,88 18611,19 30293,47 26808,47 32015,47 7460,12 23558,09	35,11 39,333 52,164 64,67 78,465 94,23 111,473 127,820 153,35 165,174	105,33 275,330 678,129 905,38 1176,971 1696,14 1337,679 1406,029 306,7 825,87	427,113 1245,869 3387,256 4947,901 6985,318 10863,77 9196,547 10327,28 2396,860 6842,333	1731,94 5637,56 16919,35 27040,28 41457,87 69582,49 63226,26 75853,94 18731,46 56688,73
S			609,95	3827,91	24675,57	163073,1	921,789	8713,56	56620,27	376869,9

Получим систему уравнений:

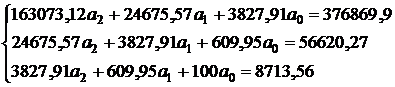
Решим полученную систему:

;

;

;

;

;

;

.

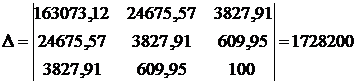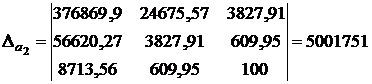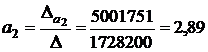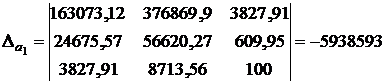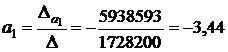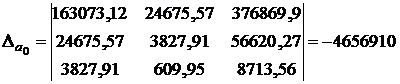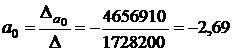Получаем выборочное уравнение регрессии 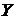на :

.

Рисунок 2 – Квадратичная линия регрессии

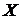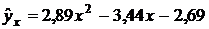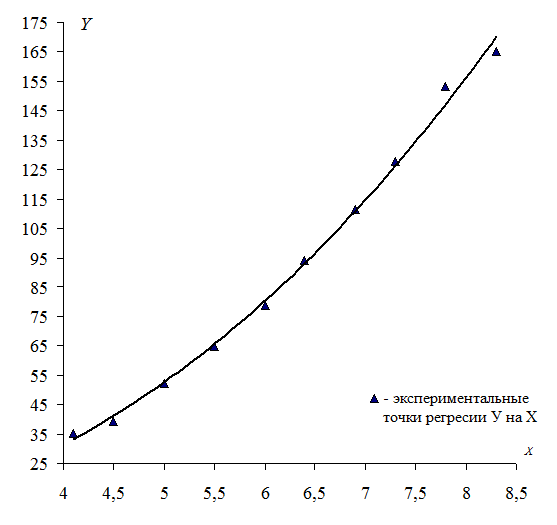
Точечные оценки параметров уравнения регрессии 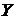на 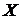генеральной совокупности.

; ; .

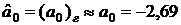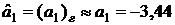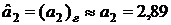Нахождение средней квадратической ошибки уравнения

Так как значения 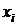известны без ошибок, а значения независимы и равноточны, то оценка дисперсии вычисляется по формуле:

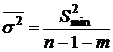, где 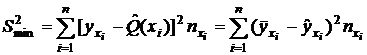, (23)

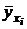– фактические значения результативного признака, полученного по данным наблюдений, 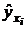– значения результативного признака, рассчитанного по уравнению регрессии и полученного подстановкой значений факторного признака в уравнение регрессии: 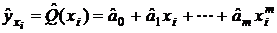. В нашем примере .

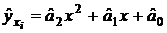Средняя квадратическая ошибка уравнения регрессии: .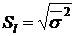

Для нахождения оценки дисперсии 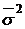величины составим таблицу:

№
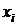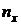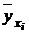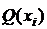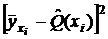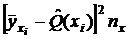	4,055 4,525 4,995 5,465 5,935 6,405 6,875 7,345 7,815 8,285		35,11 39,3329 52,1638 64,67 78,4647 94,23 111,4733 127,8209 153,35 165,174	30,8811 40,9186 52,2328 64,8238 78,6916 93,8362 110,2547 127,9559 146,9309 167,1827	17,8832 2,5143 0,0048 0,0236 0,05149 0,1551 1,4778 0,01822 41,2047 4,0350	53,6497 17,6001 0,0618 0,3311 0,7723 2,7918 17,7335 0,2004 82,4094 20,1752

.

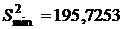
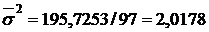Средняя квадратическая ошибка уравнения регрессии

.

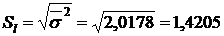Сравним полученную величину со средним квадратическим отклонением результативного признака 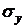, получим 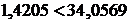, т.е. 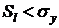, следовательно, использование уравнения регрессии является целесообразным.

Интервальные оценки параметров квадратичной линии регрессии генеральной совокупности

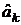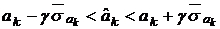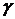Доверительные интервалы для коэффициентов при заданной доверительной вероятности имеют вид: , где определяется из таблицы для закона распределения Стьюдента по выходным величинам и числу степеней свободы .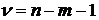

В данном случае 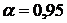, , 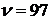отсюда .

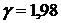Оценки 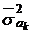коэффициентов 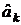определяются формулами

,

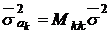где 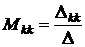, 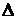– определитель системы (22), 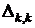– алгебраическое дополнение элемента 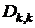в определителе .

;

;

;

; ;

;

.

;

;

;

;

;

;

.

;

;

;

;

;

;

.

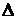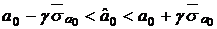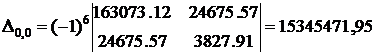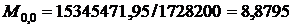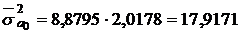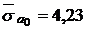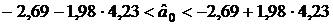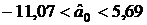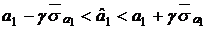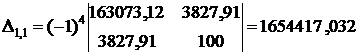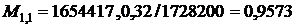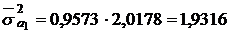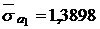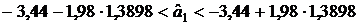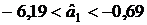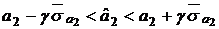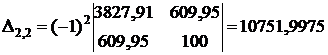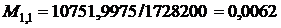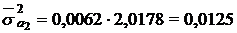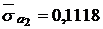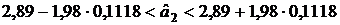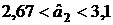Нахождение коэффициента детерминации

Коэффициент детерминации, интегрально характеризующий точностные свойства уравнения регрессии, определяем по формуле (21).

, , ,

.

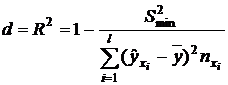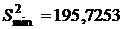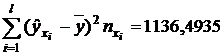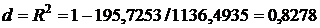Сравним 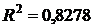с 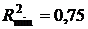. 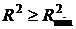– следовательно, полученная регрессионная модель работоспособна.