После этого из второго уравнения определим

5.2. Непрерывно распределенная нагрузка из параллельных сил.

На практике, кроме сил, действие которых сосредоточено в одной точке, часто встречаются силовые нагрузки, действие которых распределено вдоль линии, по поверхности или по объему тела. Такие силовые воздействия называются непрерывно распределенными нагрузками. Их действие на тело характеризуется интенсивностью q, которая в зависимости от вида нагрузки в системе СИ выражается в н/м, или Далее ограничимся рассмотрением простейшего вида непрерывно распределенной нагрузки: нагрузки из параллельных сил, непрерывно распределенной вдоль отрезка прямой линии. Пусть нагрузка распределена вдоль отрезка АВ. Направим вдоль этого отрезка ось x и построим график интенсивности действующей нагрузки q(x) (см. рис. 74). Стрелками под графиком покажем направление сил нагрузки. Получившуюся геометрическую фигуру называют эпюрой непрерывно распределенной нагрузки.

Рис. 74.

Докажем теперь одну из важных теорем статики.

Теорема Вариньона.

Если система сил имеет равнодействующую, то векторный момент равнодействующей силы относительно любого центра равен геометрической сумме векторных моментов всех сил системы, вычисленных относительно того же центра.

Доказательство.

Пусть система сил имеет равнодействующую силу . Это можно выразить соотношением эквивалентности

Добавим к системе сил силу равную по величине и направленную в противоположную сторону вдоль линии действия Тогда соотношение эквивалентности для полученной системы сил перепишется в виде

Это означает, что система сил является уравновешенной. Для такой системы сил справедливо уравнение равновесия (117):

Учитывая, что отсюда получим

(119)

Это равенство выражает утверждение теоремы.

Если векторное равенство (119) записать в проекциях на выбранные оси координат, то получим, что аналогичная теорема справедлива не только для векторных моментов сил, но и для моментов сил относительно осей, а также для алгебраических моментов сил в случае рассмотрения плоской системы сил.

Покажем теперь, как рассматриваемую непрерывно распределенную нагрузку заменить равнодействующей силой. Из школьного курса физики известно, что две одинаково направленные параллельные силы имеют равнодействующую, равную по величине сумме этих сил и направленную в ту же сторону.

Рис. 75.

Разобьем отрезок длиной l , на котором распределена нагрузка, на элементарные участки длиной dx. Действие нагрузки на каждом из таких участков может быть выражено силой (см. рис. 75). Суммируя такие силы и переходя к пределу при для величины равнодействующей силы получим

(120)

Для нахождения точки приложения равнодействующей силы применим теорему Вариньона для алгебраических моментов относительно точки О. После предельного перехода при получим (см. рис. 75)

Отсюда найдем расстояние от точки О до точки приложения равнодействующей силы

(121)

Рассмотрим далее на простейших примерах, как с помощью формул (120), (121) можно непрерывно распределенную нагрузку заменить равнодействующей силой.

1. Найдем равнодействующую силу для нагрузки с постоянной интенсивностью q=const, непрерывно распределенной на отрезке длиной l (см. рис. 76)

Рис. 76.

Величину равнодействующей силы вычислим по формуле (120)

Расстояние h найдем из (121)

2. Рассмотрим непрерывно распределенную нагрузку, интенсивность которой на отрезке возрастает по линейному закону от 0 до (см. рис. 77).

Рис. 77.

Величина равнодействующей найдется по формуле (120)

Для расстояния h из (121) получим

5.3. Равновесие системы тел.

Пусть в равновесии находится составная конструкция, состоящая из n твердых тел определенным образом соединенных друг с другом. Для того, чтобы составить полную систему независимых уравнений равновесия такой конструкции, нужно поочередно в качестве объекта равновесия выбрать каждое из тел конструкции, в соответствии с видом действующей системы сил записать для каждого тела независимые уравнения равновесия (см. табл. 1) и после этого все полученные уравнения равновесия объединить в одну общую систему уравнений.

В процессе решения задачи при обозначении на рисунках реакций внутренних связей (сил взаимодействия между телами конструкции) следует учитывать аксиому равенства действия и противодействия.

Обозначим через m число независимых уравнений равновесия составной конструкции. Пусть в местах соединения тел, входящих в конструкцию, во внешних опорах имеется k независимых компонент реакций внутренних и внешних связей. В зависимости от соотношения между m и k в механике принята следующая классификация конструкций.

Если m=k, то конструкция называется статически определимой. Для статически определимой конструкции все реакции внешних и внутренних связей можно найти из уравнений статики. Число независимых уравнений совпадает с числом неизвестных реакций.

Если m<k, то конструкция называется статически неопределимой. Для статически неопределимой конструкции из уравнений статики реакции связей найти не удается, так как число независимых уравнений равновесия меньше числа неизвестных реакций. Для изучения равновесия таких конструкций к уравнениям равновесия статики добавляют k-m уравнений совместности деформаций, изучаемых в сопротивлении материалов.

Если m>k, то конструкция называется механизмом с (m-k) степенями свободы. Равновесие механизма всегда будет шатким (неустойчивым). Для его реализации внешние активные силы не могут быть произвольными, а должны удовлетворять m-k условиям, вытекающим из уравнений равновесия.

Приведем примеры, поясняющие введенную классификацию составных конструкций.

Рассмотрим находящуюся в равновесии конструкцию, состоящую из двух стержней АС

и ВС, соединенных в точке С с помощью шарнира (см. рис. 78). В качестве внешних опор

Рис. 78.

выступают жесткая заделка в точке А и подвижная шарнирная опора в точке В. Внешними нагрузками являются сила 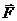, приложенная к стержню АС и пара сил с моментом М , приложенная к стержню ВС. В соответствии с изложенной методикой выберем в качестве объектов равновесия поочередно стержни АС и ВС, обозначив действующие на каждый из них внешние силы, включая реакции связей (см. рис. 79, 80).

Рис. 79.

.

Рис. 80.

Отметим, что соединительный шарнир в точке С эквивалентен неподвижному, поэтому его реакцию раскладываем на две составляющих. В соответствии с аксиомой равенства действия и противодействия силы действующие в точке С на стержень АС со стороны стержня ВС (см. рис. 79), и такие же по величине силы действующие на стержень ВС со стороны стержня АС (см. рис. 80), направлены в противоположные стороны.

На каждое из тел конструкции действует произвольная плоская система сил, поэтому общее число независимых уравнений равновесия составной конструкции будет m=3+3=6. Независимыми компонентами реакций связей здесь являются их количество k=6. Таким образом, в данном случае m=k и конструкция, изображенная на рис. 78, является статически определимой.

Рассмотрим далее конструкцию, в которой, по сравнению с ранее рассмотренной (см. рис. 78), подвижная шарнирная опора в точке В заменена неподвижным цилиндрическим шарниром, а остальные элементы конструкции и внешние нагрузки остались неизменными (см. рис. 81).

Рис. 81.

Выбрав в качестве объектов равновесия стержни АС и ВС, обозначим действующие на них внешние силы (см. рис. 82,83). Силы, приложенные к стержню АС, остались такими

Рис. 82.

Рис. 83.

же. Для стержня ВС изменится реакция в опоре В, которую в данном случае следует разложить на две составляющих На каждое из тел конструкции по-прежнему действует произвольная плоская система сил. Общее число независимых уравнений равновесия будет m=6. Независимыми компонентами реакций связей в данном случае будут их количество k=7. Получили m<k, следовательно, конструкция, изображенная на рис. 81, будет статически неопределимой.

Рассмотрим третий вариант составной конструкции, в которой по сравнению с исходной конструкцией, изображенной на рис. 78, жесткая заделка в точке А заменена неподвижным цилиндрическим шарниром, а остальные элементы конструкции и внешние нагрузки остаются без изменения (см. рис. 84). Считаем, что конструкция находится в равновесии.

Рис. 84.

Выбрав в качестве объектов равновесия стержни АС и ВС, обозначим действующие на них внешние силы (см. рис. 85,86). Как и в двух предыдущих случаях на каждое из тел

Рис. 85.

Рис. 86.

действует плоская произвольная система сил и общее число независимых уравнений равновесия этой конструкции будет m=6. Независимыми компонентами реакций связей здесь являются их количество k=5. Получили m>k и m-k=1, следовательно, изображенная на рис. 84 конструкция является механизмом с одной степенью свободы.