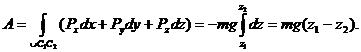Тогда из формулы (83) для кинетической энергии тела получим

Поступательное движение.

При поступательном движении все точки тела в любой момент времени имеют одинаковые скорости

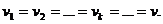
Тогда из формулы (83) для кинетической энергии тела получим

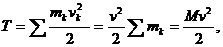(84)

где М – масса тела; v – общая скорость всех точек тела.

Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для точки, масса которой равна массе всего тела.

Вращательное движение.

При вращательном движении тела скорость каждой точки тела можно вычислить по формуле (см. рис. 14)

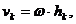
где 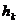- расстояние от k-й точки до оси вращения. Тогда из формулы (83) для кинетической энергии тела получим

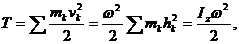(85)

где 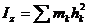- момент инерции тела относительно оси вращения.

Формулы (84) и (85) имеют одинаковую структуру. Сравнивая их, можно сделать вывод, что, если масса тела М является мерой инертности тела при поступательном движении, то осевой момент инерции тела 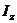является мерой инертности тела при вращении вокруг неподвижной оси.

Плоское движение.

При вычислении кинетической энергии тела в этом случае удобно с центром масс тела мысленно связать поступательно перемещающуюся подвижную систему координат 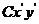(см. рис. 67) и разложить плоское движение на два более простых:

- поступательное со скоростью ,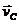

- вращательное с угловой скоростью ω относительно подвижной оси 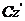, перпендикулярной плоскости рисунка.

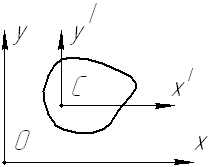
Рис. 67.

Тогда кинетическая энергия тела при плоском движении может быть вычислена по формуле

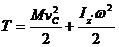(86)

где 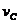- скорость центра масс тела, 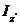- момент инерции тела относительно оси проведенной через центр масс перпендикулярно плоскости движения, ω – угловая скорость тела при плоском движении.

4.4.2. Работа и мощность силы.

Элементарной работой силы 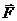на бесконечно малом перемещении и ds ее точки приложения называется скалярная величина

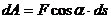, (87)

где α – угол между вектором силы и вектором скорости точки (см. рис. 68).

Рис. 68.

В зависимости от величины угла α элементарная работа может быть как положительной, так и отрицательной. При dA>0 сила ускоряет движение точки, при dA<0 – замедляет движение.

Учитывая, что

ds=dr=v∙dt,

для элементарной работы можно записать несколько эквивалентных выражений:

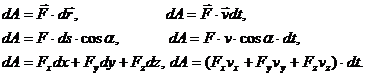(88)

Полной работой (или просто работой) силы на конечном перемещении (см. рис. 68) ее точки приложения называется скалярная величина

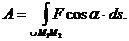(89)

Согласно формулам (88) для полной работы силы можно также записать эквивалентные выражения

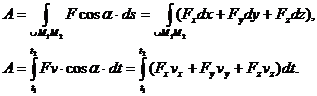(90)

Здесь 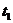и 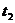- моменты времени, когда точка находится в положениях 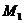и 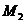, соответственно.

Отметим частный случай, когда вычисление работы существенно упрощается. Если проекция силы на направление скорости при движении не изменяется 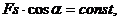то из (89) получим

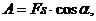(91)

где s – путь, пройденный точкой.

Мощностью силы называется отношение элементарной работы к промежутку времени, за который эта работа совершена

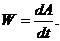(92)

Учитывая, что 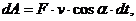выражение для мощности можно переписать в виде

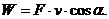(93)

Формула (93) удобна при практических вычислениях. Поясним физический смысл введенного понятия: мощность характеризует работоспособность источника силы за единицу времени.

4.4.3. Примеры вычисления работы силы.

Работа силы в общем случае вычисляется достаточно сложно. Для ее вычисления надо знать характеристики движения точки приложения силы и вычислить соответствующий интеграл. Рассмотрим далее несколько примеров, когда работа силы вычисляется сравнительно просто.

Сила тяжести.

Сила тяжести 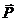тела приложена в его центре тяжести и направлена вертикально вниз. Вблизи поверхности Земли центр тяжести совпадает с центром масс, а сила тяжести постоянна и равна mg. Выберем систему координат Oxyz так, чтобы ось Oz была направлена вертикально вверх (см. рис. 69). Тогда проекции силы тяжести на оси координат будут равны

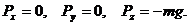
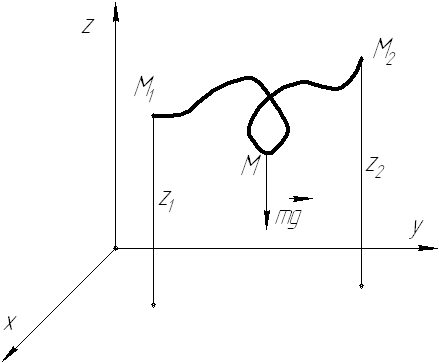
Рис. 69.

Вычислим работу силы тяжести при произвольном перемещении тела, когда его центр тяжести С перемещается по некоторой траектории из положения 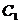в положение :

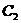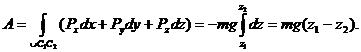
Линейная сила упругости.

Линейной силой упругости называется сила, действующая со стороны какого-либо упругого тела (например, пружины), величина которой изменяется по закону Гука:

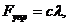
где 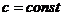- коэффициент жесткости, λ – деформация упругого тела.

Приведем без вывода формулу для работы линейной силы упругости на произвольном перемещении ее точки приложения

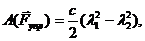(95)

где 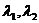– деформация упругого тела в начальном и конечном положении, соответственно.

В двух приведенных примерах работа силы не зависит от формы траектории точки приложения, а полностью определяется ее начальным и конечным положениями. Такие силы называются потенциальными (или консервативными). К числу потенциальных сил также относятся сила всемирного тяготения, сила Кулона, действующая на заряд, помещенный в электрическое поле и др.

Идеальные связи.

Связи, для которых суммарная работа их реакций равна нулю на любом перемещении несвободного тела, называются идеальными.

Рассмотрим несколько примеров идеальных связей.

а) Гладкая поверхность при скольжении по ней несвободного тела.

Реакция такой поверхности 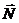перпендикулярна касательной плоскости, проведенной в точке контакта с несвободным телом, а скорость точки контакта лежит в этой касательной плоскости, то есть, реакция всегда перпендикулярна скорости ее точки приложения. Тогда

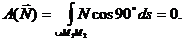
б) Шероховатая поверхность при качении по ней колеса без проскальзывания и отсутствии сопротивления качению.

Реакцию такой поверхности удобно раскладывать на две составляющие: нормальную реакцию 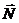и силу трения 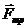(см. рис. 70). Точка приложения этих реакций в данном

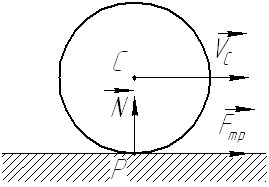
Рис. 70.

случае является мгновенным центром скоростей и имеет нулевую скорость 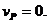Тогда

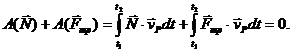
К числу идеальных связей относятся также гибкая нерастяжимая нить, шарнирные опоры при отсутствии в них трения и др.

Поступательное движение.

При поступательном движении все точки тела в любой момент времени имеют одинаковые скорости

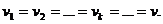
Тогда из формулы (83) для кинетической энергии тела получим

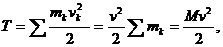(84)

где М – масса тела; v – общая скорость всех точек тела.

Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для точки, масса которой равна массе всего тела.

Вращательное движение.

При вращательном движении тела скорость каждой точки тела можно вычислить по формуле (см. рис. 14)

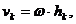
где 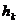- расстояние от k-й точки до оси вращения. Тогда из формулы (83) для кинетической энергии тела получим

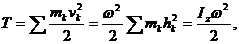(85)

где 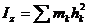- момент инерции тела относительно оси вращения.

Формулы (84) и (85) имеют одинаковую структуру. Сравнивая их, можно сделать вывод, что, если масса тела М является мерой инертности тела при поступательном движении, то осевой момент инерции тела 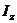является мерой инертности тела при вращении вокруг неподвижной оси.

Плоское движение.

При вычислении кинетической энергии тела в этом случае удобно с центром масс тела мысленно связать поступательно перемещающуюся подвижную систему координат 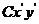(см. рис. 67) и разложить плоское движение на два более простых:

- поступательное со скоростью ,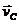

- вращательное с угловой скоростью ω относительно подвижной оси 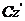, перпендикулярной плоскости рисунка.

Рис. 67.

Тогда кинетическая энергия тела при плоском движении может быть вычислена по формуле

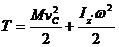(86)

где 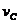- скорость центра масс тела, 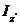- момент инерции тела относительно оси проведенной через центр масс перпендикулярно плоскости движения, ω – угловая скорость тела при плоском движении.

4.4.2. Работа и мощность силы.

Элементарной работой силы 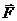на бесконечно малом перемещении и ds ее точки приложения называется скалярная величина

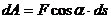, (87)

где α – угол между вектором силы и вектором скорости точки (см. рис. 68).

Рис. 68.

В зависимости от величины угла α элементарная работа может быть как положительной, так и отрицательной. При dA>0 сила ускоряет движение точки, при dA<0 – замедляет движение.

Учитывая, что

ds=dr=v∙dt,

для элементарной работы можно записать несколько эквивалентных выражений:

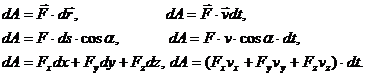(88)

Полной работой (или просто работой) силы на конечном перемещении (см. рис. 68) ее точки приложения называется скалярная величина

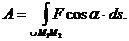(89)

Согласно формулам (88) для полной работы силы можно также записать эквивалентные выражения

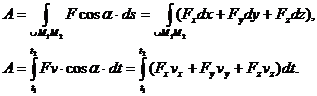(90)

Здесь 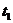и 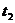- моменты времени, когда точка находится в положениях 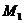и 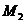, соответственно.

Отметим частный случай, когда вычисление работы существенно упрощается. Если проекция силы на направление скорости при движении не изменяется 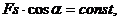то из (89) получим

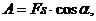(91)

где s – путь, пройденный точкой.

Мощностью силы называется отношение элементарной работы к промежутку времени, за который эта работа совершена

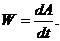(92)

Учитывая, что 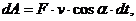выражение для мощности можно переписать в виде

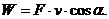(93)

Формула (93) удобна при практических вычислениях. Поясним физический смысл введенного понятия: мощность характеризует работоспособность источника силы за единицу времени.

4.4.3. Примеры вычисления работы силы.

Работа силы в общем случае вычисляется достаточно сложно. Для ее вычисления надо знать характеристики движения точки приложения силы и вычислить соответствующий интеграл. Рассмотрим далее несколько примеров, когда работа силы вычисляется сравнительно просто.

Сила тяжести.

Сила тяжести 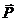тела приложена в его центре тяжести и направлена вертикально вниз. Вблизи поверхности Земли центр тяжести совпадает с центром масс, а сила тяжести постоянна и равна mg. Выберем систему координат Oxyz так, чтобы ось Oz была направлена вертикально вверх (см. рис. 69). Тогда проекции силы тяжести на оси координат будут равны

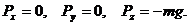
Рис. 69.

Вычислим работу силы тяжести при произвольном перемещении тела, когда его центр тяжести С перемещается по некоторой траектории из положения 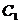в положение :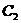