Характеристическое уравнение и собственный вектор линейного оператора.

Определение. Характеристическим уравнением линейного оператора f называется уравнение вида 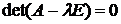, где λ –любое действительное число, А – матрица линейного оператора, Е – единичная матрица того же порядка.

Многочлен 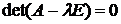называется характеристическим многочленом 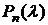матрицы А (линейного оператора f). В матричном виде характеристическое уравнение имеет следующий вид:

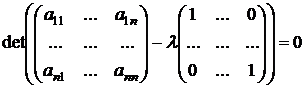или

.

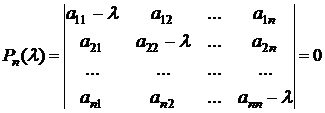Следовательно, приравнивая характеристический многочлен к нулю, получаем уравнение степени n, где в качестве неизвестного выступает λ, получаем значения его корней – характеристических чисел данной матрицы. Характеристические корни играют большую роль во многих разделах математики. Рассмотрим одно из применений характеристических корней – очень важный инструмент при исследовании линейных пространств, а также при решении многих прикладных задач линейной алгебры.

Набор всех корней характеристического уравнения называют спектром оператора f (каждый корень рассматривают с той кратностью, которую он имеет в характеристическом уравнении).

Пример. Найти характеристические корни матрицы .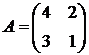

Составим матрицу

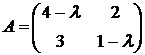
Приравнивая характеристический многочлен к нулю, получаем квадратное уравнение

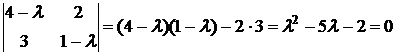. Тогда корни уравнения равны .

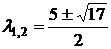Определение. Пусть f линейный оператор пространства 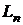и 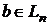- некоторый ненулевой вектор, для которого справедливо равенство

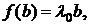
где 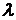- действительное число. Тогда вектор 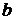называют собственным вектором оператора и матрицы его задающего, 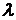- собственным значением, или собственным числом преобразования. При этом говорят, что собственный вектор 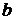относится к собственному значению .

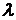Собственные векторы играют большую роль, как в самой математике, так и в ее приложениях. Например, резонанс, при котором собственные частоты колебаний системы, совпадают с частой колебаний внешних сил. В математике собственные векторы полезны при решении систем дифференциальных уравнений.

Теорема. Если линейный оператор f в базисе 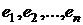(первый базис) имеет матрицу А и в базисе 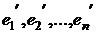(второй базис) – матрицу В, то имеет место равенство: .

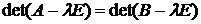Следовательно, при переходе к новому базису характеристический многочлен линейного оператора не меняется.

◌ Если Т – матрица перехода от первого базиса ко второму, то 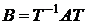. Тогда преобразуем правую часть равенства ●

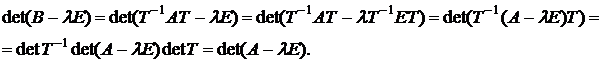Теорема. Для того чтобы число λ₀ из поля Р было собственным значением вектора пространства L_n над Р необходимо и достаточно, чтобы число λ₀ являлось характеристическим корнем оператора f.

Док-во. I. Необходимость. Пусть λ₀ собственное значение оператора f, тогда вL_n существует собственный вектор 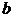, такой, что .

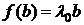Пусть 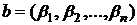– его координатная строка в некотором базисе, тогда

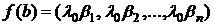(1)

С другой стороны, т.к. 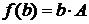, где 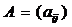– матрица линейного оператора в заданном базисе, то

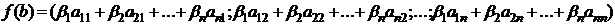(2)

Приравняв правые части (1) и (2) получим:

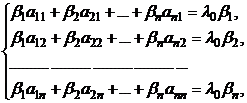(3)

Равенства (3) означают, что числовой вектор с координатами 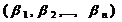является решением следующей системы уравнений 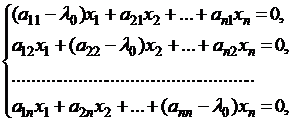(4).

(4)

Вектор 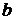отличен от нулевого (т.к. он собственный), поэтому система (4) имеет ненулевое решение, следовательно ее определитель равен 0.

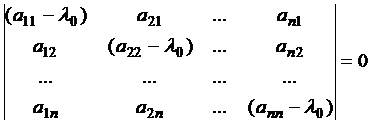(5)

а значит и транспонируемый определитель равен 0.

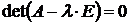(6)

Таким образом, λ₀ – корень характеристического уравнения.

II. Достаточность. Пусть λ₀ – характеристический корень оператора 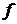в некотором базисе 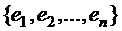. Докажем, что λ₀ является собственным значением оператора A.

Действительно, если λ₀ – характеристический корень, то будет выполняться равенство (6), а следовательно, равенство (5), а это будет означать, что система (4) имеет ненулевые решения.

Выберем какое-нибудь ненулевое решение системы(4): числовой вектор 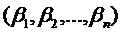. Тогда выполняются равенства (3).

Рассмотрим вектор 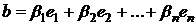, а для него будет выполняться равенство (2) и, в силу формулы 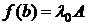, справедливо равенство (1), где 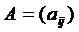– матрица оператора 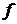в базисе В. Отсюда следует равенство 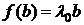, которое означает, что вектор 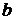является собственным вектором оператора 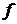, которому соответствуют собственное значение λ₀. Это и требовалось доказать. Теорема доказана.

Замечание.Для того чтобы найти собственные значения оператора, надо составить и решить уравнение (5). Чтобы найти собственные векторы оператора нужно составить систему уравнений (4) и найти фундаментальный набор решений этой системы.

Для контроля за правильностью вычисления собственных значений (они могут быть совпадающие, комплексные) используются два факта:

1) 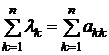, где последняя сумма след матрицы – сумма диагональных элементов.

2) .

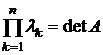Пример.Найти собственные значения и собственные векторы .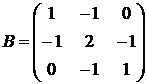

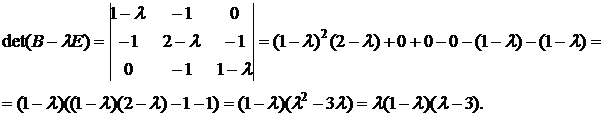Приравнивая к нулю получаем .

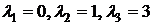Найдем собственные векторы.

1) . , .

.

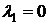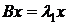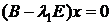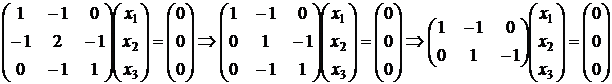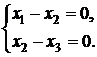
Пусть 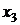- свободная переменная, тогда 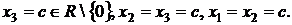Получаем вектор .

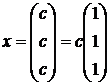2) . , .

.

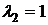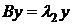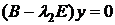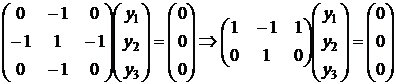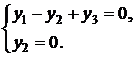
Пусть 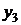- свободная переменная, тогда

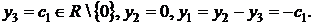Получаем вектор .

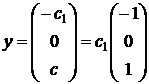3) . , .

.

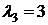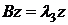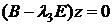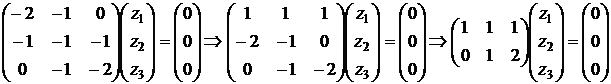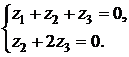
Пусть 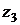- свободная переменная, тогда 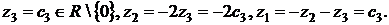Получаем вектор .

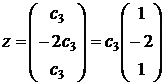Упражнение. Сделать проверку для вектора .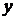

.
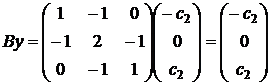