Диагональный вид матриц линейного оператора.

Пусть имеется некоторый линейный оператор с матрицей А.

Теорема (условие диагональности матрицы). Матрица линейного оператора имеет диагональный вид тогда и только тогда, когда каждый базисный вектор является собственным вектором этого оператора.

□ если матрица линейного оператора имеет диагональный вид

,

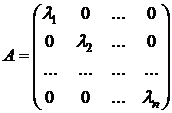то векторы соответствующего базиса 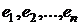могут быть представлены в виде 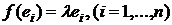, что означает, что они являются собственными векторами. И обратно, если векторы базиса являются собственными, т. е. имеет место равенство 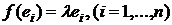, то матрица А имеет диагональный вид. ■

Определение.Приводимой к диагональному виду называется такая матрица А, для которой существует невырожденная матрица Т, для которой матрица 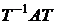является диагональной. Чтобы построить матрицу Т, надо определить собственные числа 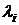из характеристического уравнения для матрицы А.

Теорема. Матрица А линейного оператора f n-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного оператора.

Доказательство основывается на предыдущей теореме и определении.

Матрица будет приводиться к диагональному виду, если все ее собственные числа 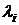попарно различны.

Действия над линейными операторами.

Определение. Произведением (композицией) линейного оператора f на линейный оператор g называется оператор, являющийся последовательным применением операторов f и g, обозначается 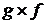, т. е. для вектора x имеем .

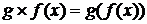Произведение линейных операторов само является линейным оператором. Действительно, для любых векторов 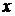и и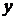сходя из определения линейного оператора имеем: .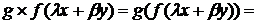

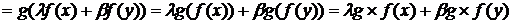Теорема. Если в некотором базисе линейные операторы f и g имеют соответственно матрицы А и В, то их произведение 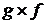имеет матрицу ВА.

Определение. Сумма линейных операторов f и g некоторого линейного пространства – это такой оператор h, что для любого вектора x выполняется равенство 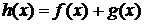. Обозначается .

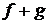Справедливо 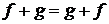. Сумма линейных операторов является линейным оператором.

Теорема. Если линейные операторы f и g в некотором базисе имеют соответственно матрицы А и В, то их сумма 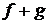в том же базисе имеет матрицу В+А.

Линейные операторы могут быть вырожденными (имеют вырожденную матрицу) и невырожденные.

Теорема. Произведение двух линейных невырожденных операторов есть невырожденный линейный оператор.

□ Если А и В матрицы операторов f и g, то матрица произведения операторов равна ВА, ее определитель равен 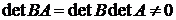, поскольку 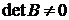и .■

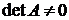Ортогональные матрицы.

Пусть имеется евклидово n-мерное пространство .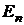

Определение. Матрица ортонормированной системы векторов 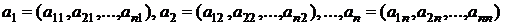называется ортогональной. Для таких ортонормированных векторов имеем

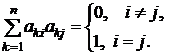
Единичные матрицы ортогональны. Например, ортогональными являются следующие единичные матрицы:

.

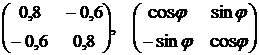Теорема. Для того чтобы матрица А была ортогональной, необходимо и достаточно, чтобы выполнялось равенство .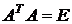

□ Если обозначить 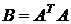, то элементы этой матрицы будут равны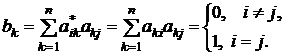

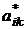элементы транспонированной матрицы. Но это означает, что 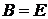или 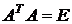. И обратно, если 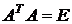, имеем равенство

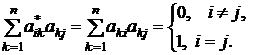
Что означает ортогональность матрицы А. ■

Следствия.

1. Модуль определителя ортогональной матрицы равен1.

2. Ортогональная матрица – невырожденная.

3. Произведение двух ортогональных матриц – ортогональная матрица.

4. Необходимым и достаточным условием ортогональности матрицы А является .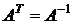

5. При транспонировании ортогональной матрицы получается ортогональная матрица.

6. Матрица, обратная ортогональной, тоже ортогональна.

Но сумма ортогональных матриц не является ортогональной.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Определение. Ортогональный оператор – это оператор евклидова пространства, матрица которого ортогональна в некотором ортонормированном базисе.

Теорема. Линейный оператор евклидова пространства является ортогональным тогда и только тогда, когда оно переводит ортонормированный базис в ортонормированный.

□ По предыдущей теореме матрица перехода от одного ортонормированного базиса к другому является ортогональной, следовательно, линейный оператор, соответствующий данной матрицы, ортогонален. И обратно, если имеется линейный оператор в некотором ортонормированном базисе с ортогональной матрицей, то из ортогональности следует, что

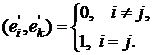
Где каждый из векторов второго базиса 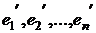равен 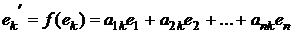( 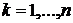), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса . ■

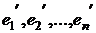Известно, что ортогональный оператор не меняет скалярного произведения векторов (следует из выражения скалярного произведения через координаты векторов в ортонормированном базисе), а следовательно, не меняется норма вектора и угол между двумя векторами.