Погрешности вычислительных операций

Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел. Если

u = ± x₁ ± x₂ ±...± x _n ,

то Du = ± D x₁ ± Dx₂ ±...± Dx _n ,

и ï Du ï£ï D x₁ï + ïDx₂ï +...+ï Dx _nï.

Предельная абсолютная погрешность

D_u =D_x1 + D_x2 +...+D_{x n}. (1)

Отсюда следует, что нельзя увеличить точность суммы за счет увеличения точности отдельного слагаемого.

Правила сложения приближенных чисел:

– выделить слагаемое (слагаемые), десятичная запись которого обрывается ранее других, и оставить его без изменения;

– остальные слагаемые округлить по образцу выделенного, сохраняя один или два запасных знака;

– произвести сложение, учитывая все сохраненные знаки;

– результат округлить на один знак.

Потеря точности при вычитании близких приближенных чисел. Определим предельную относительную погрешность разности двух приближенных чисел. Пусть u = x₁ – x₂. Используя (1.7), получим

D_u = D_x1 + D_x2.

Предельная относительная погрешность

d _u = D _u / A, (2)

где А – точное значение абсолютной величины разности u.

Если уменьшаемое и вычитаемое – близкие числа, то А будет мало и сильно увеличит предельную относительную погрешность разности.

Рассмотрим пример.

Пусть x₁ = 47,132 и x₂ = 47,111 заданы с пятью верными знаками.
Разность u = x₁ – x₂ = 0,021. Предельные абсолютные погрешности
D_x1 = D_x2 = 0,0005. Предельная абсолютная погрешность разности по (1) равна D_u = D_x1 + D_x2 = 0,001.

Предельные относительные погрешности:

d _x1 = 0,0005/47,132 » 0,00001;

d _x2 = 0,0005/47,111 » 0,00001;

d _u = 0,001/0,021 » 0,05.

Предельная относительная погрешность разности примерно в 5000 раз больше предельной относительной погрешности исходных данных этого примера.

Отсюда следуют правила для вычислений:

– следует по возможности избегать вычитания близких приближенных чисел;

– при необходимости такого вычитания следует уменьшаемое и вычитаемое брать с достаточным числом запасных верных знаков.

Определим предельную относительную погрешность произведения нескольких приближенных чисел. Относительная погрешность произведения нескольких приближенных чисел не превышает суммы относительных погрешностей этих чисел:

d £ d₁ + d₂ +...+ d _n ,

отсюда предельная относительная погрешность произведения u = x₁ x ₂...x _n следующая:

d _u= d _x1 + d _x2 + ... + d _xn, (3)

а предельная абсолютная погрешность

D_u = ïuï d _u. (4)

В частном случае умножения точного числа k на приближенное число х

u = kx,

d _u = d _x ,

D_u = ï k ïD_x.

В этом частном случае относительная предельная погрешность не изменяется, а абсолютная предельная погрешность увеличивается в ïkï раз.

Практические правила при умножении приближенных чисел:

– округлить приближенные числа так, чтобы каждое содержало на одну значащую цифру больше, чем число верных цифр в наименее точном сомножителе;

– в результате умножения сохранить столько значащих цифр, сколько верных цифр имеется в наименее точном из сомножителей.

Для частного u = x/y также верно соотношение типа (3), т.е. d_u = d_x + d_y.

Если делимое и делитель имеют по меньшей мере m верных цифр, то запредельную относительную погрешность может быть принята величина

d _u = 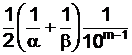, (5)

где a и b – первые значащие цифры делимого и делителя соответственно.

При возведении приближенного числа в степень m предельная относительная погрешность возрастает в m раз. При извлечении корня
m-й степени из приближенного числа предельная относительная погрешность уменьшается в m раз.

Общая формула для вычисления погрешности.

Если задана дифференцируемая функция u = f (x₁, x₂, ... x _n) и ï Dx _i ï (i = 1, 2, ...n) – абсолютные погрешности аргументов, то предельная погрешность функции

Du = 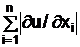Dx_i , (6)

а предельная относительная погрешность

du = Dx_i . (7)