Понятие системы счисления. Классификация систем счисления. Характеристика непозиционных систем счисления.

Понятие системы счисления. Классификация систем счисления. Характеристика непозиционных систем счисления.

Система счисления - Совокупность символов (цифр) и правил их использования для представления чисел.

Число – это последовательность цифр. Цифра – это условный знак, который используется для записи числа.

Существует два вида СС: Позиционные (Значение цифры зависит от ее положения в числе) и непозиционные (не зависит).

Непозиционные СС – значение цифр не зависит от ее положение в числе. Примером такой СС является римская СС, в ней в качестве цифр используются некоторые буквы: I-1, V-5, X-10, L-50, C-100, D-500, M-1000. Значение числа берется как сумма представляющих его цифр. Если меньшая цифра встречается перед большей, то в качестве значений берется разность этих цифр. Разность между меньшими и большими цифрами должна быть не более одного порядка. Пример: 32 -> XXXII. Операций в римской СС нет.

Понятие систем счисления. Запись чисел в позиционных системах счисления. Алгоритмы перевода целой части между системами счисления с различными основаниями.

Система счисления - Совокупность символов (цифр) и правил их использования для представления чисел.

Число – это последовательность цифр. Цифра – это условный знак, который используется для записи числа.

В позиционной СС количественное значение цифры зависит от ее позиции в числе. Позиция цифры называется разрядом. Разряд числа возрастает с право на лево.

Для задания любой СС нужно указать:

· Базис – это последовательность чисел каждое из которых задает значение цифры по ее положению в числе.

· Алфавит – это совокупность различных цифр, которая используется для записи чисел.

· Основание – это знаменатель геометрической прогрессии числа, который образует базис.

(10-ая СС: Алфавит: 0, 1, 2, …, 9; Базис: … , 10^-2, 10^-1, 1, 10¹, 10², … ; Основание: 10.)

Правила:

1. В СС с основание р в алфавите ровно р цифр, в качестве цифр выступают символы от 0 до (р-1).

2. если СС имеет основание <= 10 , то тогда используются арабские цифры.

3. Если основание >= 10 по <=36, то к арабским цифрам добавляются символы латинского алфавита.

4. Если > 36, то правило однозначно не определенно.

5. Для того что бы различить числа в разных СС, после записи числа в качестве индекса указывается основание СС, основание десятичной СС может не указываться.

Для записи любых чисел позиционной СС используется свернутая и развернутая форма:

X_p=a_n-1, a_n-2… a₂a₁a₀ – Свернутая.

X_p=a_n-1*p^n-1+a_n-2*p^n-2+ … +a₂*p²+a₁*p¹+a₀ – Развернутая.

Правила проведения операций сложения и вычитания в позиционных системах счисления.

Сложение двух чисел в системе счисления с основанием N осуществляется поразрядно от младших разрядов к старшим (“справа налево”, если смотреть на запись числа). Когда сумма данного разряда S не превышает значение N, результат сложения является окончательным. Если же S >N, то происходит перенос в старший (“более левый”) разряд, причём каждая единица переноса уменьшает значение S на величину N.

+

Составляем таблицу сложения (Сложение каждой цифры алфавита с каждой другой цифрой алфавита). Пример двоичная СС:

Понятие смешанной системы счисления, их назначение. Алгоритмы перевода между смешанными системами счисления.

СС с основаниями P и Q, называются смешанными, если P^m=Q, где m – некоторое натуральное число. СС P-Q это позиционная СС, в которой каждая цифра в записи числа, записана в СС Q заменяется на m-числовой эквивалент с СС с основанием P.

Алгоритм перевода из P->Q:

1. Нужно разбить запись числа в СС с основанием P на группы по m цифр, начиная с правого края числа.

2. Если при таком разбиение с лева не достаточно цифр, для формирования группы из m, то с лева дописываются не значимые 0.

3. Каждая группа из m цифр заменяется на 1 цифру в СС с основанием Q.

1011001₂=А₈ 111 100 111₂=747₈

001 011 001₂=131₈ 0001 1110 0111₂=1E7₁₆

10-ая

2-ая

8-ая

16-ая

A

B

C

D

E

F

Перевод из Q->P

1. Заменить каждую цифру числа в СС с основанием Q, на m цифровой эквивалент в СС с основанием P.

2. Если с лева при записи образуется не значимые 0, то их можно вычеркнуть.

73₁₆=0111 0011₂

Машина Тьюринга.

В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Машина имеет головку для чтения записей информации, эта головка, обозревает некоторую ячейку в результате, либо считывается либо записывается информация в ячейку. М – это считывающая головка.

М

Машина обладает внутренней памятью, она может иметь К-состояний. Состояние внутреннее памяти = состоянию машины Тьюринга.

Машина имеет собственную программу для функционирования (набор команд = программа). Какой символ прочитан с ленты? В каком состоянии находится машина?

Результат: - Символ, который записывается в ячейку;

- Возможное изменение состояний машины;

- Возможное перемещение читающей головки.

Команда имеет вид: a q₁ b q₂ D

a – Символ который читается с ленты, q₁ – начальное состояние, b – символ, который записывается, q₂ – новое состояние, D – возможное перемещение читающей головки. D={L, R, S} L – переместится на одну ячейку в лево, R – вправо, S – остаться на месте.

Символы, это символы из некоторого алфавита, которые остаются вместе с программой. A={a₁, … , a_n, e}, где e – пустое значение. Q={q₁, …, q_k}, k возможных состояний.

Для того что бы определить машину Тьюринга, нужно определить: Алфавит; Состояние; Программу.

Способы записи машины Тьюринга:

1. Двумерная таблица. По строкам таблицы записываются все символы алфавита, по столбцам – состояние машины. Внутри это результат работы, если не входе определен символ и определено состояние.

	q1	…	qk
a1	bq2D
…
an

2. Граф. Строиться из точек и дуг направления: Точки – Состояние машины Тьюринга, Дуги – Переход машины из одного состояния в другое, причем все дуги являются помеченными.

Обозначение: - Начальный символ

- Конечный символ

- Направления перемещения читающей головки.

a:bD

q₁ q₂

Дополнительные условия машины Тьюринга:

1. Для некорректных исходных данных программы для машины Тьюринга должны зациклиться.

· Данные считаются корректными, если в начальный момент времени читающая головка находиться на единице, входные данные.

· Исходные данные должны состоять только из алфавита машины

· Входные данные должны отвечать дополнительным условиям задачи.

2. После завершения работы алгоритма машины Тьюринга, читающая головка должна вернуться под первый символ результата.

Тезис Тьюринга – Любой не формальный алгоритм может быть записан с помощью машины Тьюринга, которая дает один и тот же результат при одинаковых исходных данных.

Композиции машин Тьюринга.

По другому их можно назвать операции над машиной Тьюринга.

ü ИТЕРАЦИЯ, последовательное соединение.

Имеются две машины Тьюринга, Т1 и Т2, задается некоторое начальное состояние Т1 и некоторая комбинация на ленте. Эта программа выполняется и в один этап, мы получаем результат. Результат исходные данные для Т2 и после этого выполниться машина Т2.

Алгоритм работы последовательного соединения.

1. Механически объединить в одну таблицу две программы.

2. Заменить конечное состояние Т1 на начальное состояние Т2.

3. Нужно заменить клетки Т1, которые означают завершение первой программы, команды следующего вида. i p₁ S

i – Символ который стоит в строке, p₁ – Начальное состояние, S – движение остаться на месте.

ü ПОВТОРЕНИЕ машины Тьюринга.

1. В тех машинах где встречается конечное состояние, нужно указать начальное состояние этой же машины.

2. В пустых клетках указать i q₁ S

i – Символ который соответствует строке, где записана команда, q₁ – Начальное состояние, S – движение остаться на месте.

Алгорифмы Маркова.

Нормальные алгорифмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгорифма состоит из двух частей: определения алфавита алгорифма (к словам в котором алгорифм будет применяться) и определения его схемы. Схемой нормального алгорифма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгорифма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгорифма. При этом предполагается, что вспомогательные буквы и не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгорифма в пятибуквенном алфавите | * abc может служить схема

15. Композиция Маркова

Композиции алг Маркова

Правила объединения: 1) сегм.кот выполняет операции М2 должен идти первым в записи объединеного алг. 2) строка должна защищена от обработки М2 пока не кончит М1 3) в М1 надо заменить кажд.правило вида α→.β на α→a’β а последним правилом добавить λ→a’. 4) в М2 надо заменить все λ на с’ все строки вида S₁,S₂.. на с’S₁,с’S₂.. α→β меняем на α→D’β а последним правилом добавить с’→D’

Целочисленные типы

---------------------------------------------------------------

Предопределенные целочисленные типы Таблица 4.1

---------------------T--------------------T---------------------

¦ Тип ¦ Диапазон ¦ Формат ¦

+--------------------+--------------------+---------------------+

¦ целое ¦ -32768 .. 32767 ¦ 16 бит со знаком ¦

¦ (Integer) ¦ ¦ ¦

+--------------------+--------------------+---------------------+

¦ длинное целое ¦ -2147483648 .. ¦ 32 бита со знаком ¦

¦ (Longint) ¦ ..2147483647 ¦ ¦

L--------------------+--------------------+----------------------

_____ _____

--->¦знак ¦--->¦число¦--->

¦_________¦ ¦_________¦

Операции:

· DIV, MOD

· Арифметич. (+,-,*,/)

· Сравнения (<,>,=,>=,<=,<>)

Процедуры и функции:

· математические (sqr, sqrt)

· тригонометрич. (sin, cos)

· прочие (

o pred – пред знач.

o succ – след.знач

o odd – true if nech

o inc - ++

o dec - --

33. Real

Вещественные типы

-----------------------------------------------------------------

Диапазон представления

и десятичные цифры для вещественных типов Таблица 4.2

------------------------T---------------------------T-----------

¦ Тип ¦ Диапазон ¦ Цифры ¦

+-----------------------+---------------------------+-----------+

¦ вещественное ¦2.9x10^-39 .. 1.7x10^38 ¦от 11 до 12¦

¦ (Real) ¦ ¦ ¦

L-----------------------+---------------------------+------------

[±]Z.[C]

±mE±p

Вещ.число _____ _________ ________ _____ _________

--------->¦знак ¦--->¦цел.часть¦-->.-->¦др.часть¦--->E-->¦знак ¦-->¦цел.часть¦--->

¦_________¦ ¦________________¦¦__________________________¦

Операции:

· Сравнения (<,>,=,>=,<=,<>)

· Арифметические(+,-,*,/)

Процедуры и функции:

· Все математич.

· Все тригонометрич.

· Прочие()

o Trunc – отсек. Др.часть

o Round – округл.до ближ.целого

34. Char Boolean

Логический тип

-----------------------------------------------------------------

True, False

Операции:

· логические (or, and, not)

· Сравнения (<,>,=,>=,<=,<>)

Процедуры и функции:

- False < True

- Ord(False) = 0

- Ord(True) = 1

- Succ(False) = True

- Pred(True) = False

Символьный тип (char)

-----------------------------------------------------------------

Кодировка: расположение символов по кодам их представляемых.

Условия:

· Кажд. Символ имеет свой числовой эквивалент

· Коды символов, изображ.арабские цифры идут строго последовательно, и упорядочены по возрастанию

· Любая кодировка должна содерж.символ пробела

ACSII – 256 символов

Операции:

· Сравнения (<,>,=,>=,<=,<>)

Процедуры и функции:

· Ord(A)=152

· Chr(152)=A

35. Перечисление, отрезок, множество

Отрезки типа

-----------------------------------------------------------------

ЗАПРЕЩЕНО! Использовать для Real

Type имя = min..max

pul=10..50;

color=red..black;

type matrix = array[1..m,1..n] of real;

Перечислимые типы

-----------------------------------------------------------------

имя знач.1

имя знач.2

Type имя = . . . . .

имя знач.N-1

имя знач.N

var x:имя;

Операции:

· Сравнения (<,>,=,>=,<=,<>)

Процедуры и функции:

· Pred

· Succ

· Ord

I/O – НЕТ!

Множественные типы

-----------------------------------------------------------------

Type имя = set of базовый тип

M1 = set of color;

Var x:M1;

Присваивания: x:=[red,black,green]

x:=[white]

x:=[]

Операции:

· Сложение

· Умножение

· Вычитание

· In

Проц. и Функц.: НЕТ!

I/O: НЕТ!

36. Массив Запись

Типы массив

-----------------------------------------------------------------

Type имя = array [T1] of T2

T1 – тип индекса (кроме вещ.)

T2 – тип элементов (кроме file)

Тип запись

-----------------------------------------------------------------

Type имя = record {как begin}

имя поля₁: тип₁;

имя поля₂: тип₂;

End;

Пример:

type day=1..31;

month=(янв,фкв,матр,..,дек);

data=record

d:day;

m:month;

y:integer;

end;

var x:data;

begin

x.d:=15;

x.m:=май;

x.y:=2007;

Все действия только по составляющим полям

Проц., Функций – НЕТ!!!

I/O – по полям!

37. Тип Файл

-----------------------------------------------------------------

Файлы:

Текстовые

Типизированные

Нетипизированные

s1 s2 s3 s4 s5¶ <--- мкс

p1 p2 p3 p4 p5

. . . . . . .

z1 z2 z3 z4 z5¶ <---мкф

assign(F,’c:\nyana.mp3’);

reset(F)

rewrite(F)

eof(F)

eoln(F)

read(F,I)

readln(F) – переводит указатель на новую строку

append(F)

close(F)

rename(F,<new name>)

erase(F)

flush(F) – очистка буфера

fsearch(‘file.txt’,’\sub;\subd’);

seekeoln(F) – пропускает все пробелы и tab

38. Ссылки в Pascal

Type

mas = array[1..20] of integer; {базовый тип}

pm = ^mas; {тип-указатель на массив}

pin = ^integer; {тип-указатель на целое число}

Базовым типом для ссылочного типа может быть любой тип, в том числе и ещё необъявленный, что является исключением для Turbo Pascal. То есть ссылочный тип может быть объявлен раньше, чем объявлен базовый тип.

Например:

Type

pm = ^mas;

mas = array[1..20] of integer;

Имея в программе определения ссылочного типа, можно по общим правилам описать переменные этого типа (указатели). Ссылочные типы в описаниях можно задавать как посредством идентификаторов, так и явно, например:

Var

p1, p2: pin;

mm: ^mas;

После объявления переменной ссылочного типа (указателя), значение её неопределено. Значением ссылочной пременной может быть адрес переменной базового типа. Для того, чтобы определить значение ссылочной переменной, необходимо занести в неё (присвоить) адрес переменной базового типа.

Операция взятия указателя.

--------------------------

Если в программе объявлена некоторая переменная, например:

Var

i: integer;

то, как вам уже давно известно, при обращении к этой переменной по её имени мы получим содержимое этой переменной. Если же, при обращении к этой переменной, перед её именем (идентификатором) поставить специальный символ '@', то мы получим не значение данной переменной, а её адрес. Такую запись в Turbo Pascal называют операцией взятия указателя, и используют для определения ссылочных переменных:

p1 := @i; В результате образуется следующая связь:

p1 i

+-----------+ +------------+

¦указатель ------------------->¦целое ¦

+-----------+ +------------+

Операция взятия указателя допустима для любых переменных, в том числе для элементов массивов, полей записи и т.д. Например, если есть описание

var

A: array[1..10] of integer;

то обращение @A[i] имеет смысл указателя на i-ое целое в массиве A и также может учавствовать в присваивании:

p1 := @A[i];

Массивы

Массивы - это группа элементов одинакового типа (double, float, int и т.п.). Из объявления массива компилятор должен получить информацию о типе элементов массива и их количестве.

В языке СИ определены только одномерные массивы, но поскольку элементом массива может быть массив, можно определить и многомерные массивы. Они формализуются списком константных-выражений следующих за идентификатором массива, причем каждое константное-выражение заключается в свои квадратные скобки.

Каждое константное-выражение в квадратных скобках определяет число элементов по данному измерению массива, так что объявление двухмерного массива содержит два константных-выражения, трехмерного - три и т.д. Отметим, что в языке СИ первый элемент массива имеет индекс равный 0.

Примеры:

int a[2][3]; /* представлено в виде матрицы

a[0][0] a[0][1] a[0][2]

a[1][0] a[1][1] a[1][2] */

double b[10]; /* вектор из 10 элементов имеющих тип double */

int w [3][3] = { { 2, 3, 4 },

{ 3, 4, 8 },

{ 1, 0, 9 } };

В последнем примере объявлен массив w[3][3]. Списки, выделенные в фигурные скобки, соответствуют строкам массива, в случае отсутствия скобок инициализация будет выполнена неправильно.

Структуры-это составной объект, в который входят элементы любых типов, за исключением функций. В отличие от массива, который является однородным объектом, структура может быть неоднородной. Тип структуры определяется записью вида:

struct { список определений }

В структуре обязательно должен быть указан хотя бы один компонент.

Пример:

struct { double x,y; } s1, s2, sm[9];

struct { int year;

char moth, day; } date1, date2;

Объединения (смеси)

Объединение подобно структуре, однако в каждый момент времени может использоваться (или другими словами быть ответным) только один из элементов объединения. Тип объединения может задаваться в следующем виде:

union { описание элемента 1;

...

описание элемента n; };

Главной особенностью объединения является то, что для каждого из объявленных элементов выделяется одна и та же область памяти, т.е. они перекрываются.

Доступ к элементам объединения осуществляется тем же способом, что и к структурам. Тег объединения может быть формализован точно так же, как и тег структуры.

Память, которая соответствует переменной типа объединения, определяется величиной, необходимой для размещения наиболее длинного элемента объединения. Когда используется элемент меньшей длины, то переменная типа объединения может содержать неиспользуемую память. Все элементы объединения хранятся в одной и той же области памяти, начиная с одного адреса.

Пример: union { char fio[30];

char adres[80];

int vozrast;

int telefon; } inform;

union { int ax;

char al[2]; } ua;

Поиск с барьером

Барьер – дополнительный фиктивный элемент который располагается в начале или в конце массива

Const n=10;

Type vector: array [ 1..n + 1] of integer;

…

Function line_search ( a: vector; x: integer): integer;

Var I : integer;

Begin

A [ n+1] := x;

I:= 1;

While a[i] <> x do i:= i+1;

If I < n+1 then line_search:= I

Else line_search := -1 ;

End;

Двоичный поиск ( методом деления пополам)

Const n =10 ;

Type vector: array [ 1..n] of integer;

…

Function binary_search ( a: vector; x: integer ): integer;

Var I, r ,m : integer; Q: Boolean;

Begin

I:= 1;

R:= n;

Q:= false;

While ( i< r ) and ( not q ) do

Begin

M:= ( l + r ) div 2;

If a [m] = x then q:= true

Else if a[m] < x then L:= m

Else r:= m;

End;

If q then binary_search :=m

Else binary_search := -1;

End;

Списки

type Spisok=record

inf:real;

next:TSpisok;

end;

TSpisok=^Spisok;

Списки.Обход(нерекурс.вар.):

procedure Browse(head:TSpisok);

begin while head<>nil do begin

write(head^.inf);head:=head^.next;

Списки.Обход (рекурс.вар.):

procedure browse(head:TSpisok);

begin if head<>nil then begin

write(head^.inf);browse(head^.next);

Списки.Подсчёта кол-ва элем-ов:

function ength(head:TSpisok):integer;

begin if head<>nil then length:=1+length(head^.next)

else length:=0; end;

Списки.Поиск по значению:

function Find(x:real;head:TSpisok): TSpisok; begin if head<>nil then begin while (head<>nil) and (head^.inf<>x)do head:=head^.next; Find:=head;end

else Find:=nil;end;

function find(x:real; head:TSpisok): TSpisok; begin if head<>nil

then if head^.inf<>x then find:=find(x;head^.next) else find:=head; else find:=nil;end;

Списки.Вставка в список:

procedure Insert(p:TSpisok;x:real;var head:TSpisok); var q:TSpisok; begin

new(q); g^.inf:=x; if head<>nil then begin q^.next:=p^.next; p^.next:=q;

end else begin g^.next:=nil;head:=q;

Списки.Вставка в начало:

procedure Insert1(var head:TSpisok; x:real); var q:TSpisok; begin new(q);

q^.inf:=x; if head<>nil then begin

q^.next:=head; head:=q; end else begin g^.next:=nil; head:=q; end;

Списки.Вставка в конец:

procedure Insert2(var head:TSpisok; x:real); var p,q:TSpisok; begin

new(q); q^.inf:=x; if head<>nil

then begin q^.next:=nil; p:=head;

while p^.next<>nil do p:=P^.next;

p^.next:=q end else begin

g^.next:=nil; head:=q; end; end;

Списки.Удаление из списка:

procedure delete(var head:TSpisok; var p,q:TSpisok); begin if head<>nil

then begin q^.next:=p^.next;

dispose(p); end; end;

Списки.Удаление из начала:

procedure delete1(var head:TSpisok);

var q:TSpisok; begin if head<>nil

then begin q:=head; head:=head^.next; despose(q); end;

Списки.Удаление из конца:

procedure delete2(var head:TSpisok);

var p,q:TSpisok; begin if head<>nil

then begin q:=head; while q^.next<>nil do begin p:=q;

q:=q^.next; end; p^.next:=nil;

dispose(q); end; end;

Списки.Удал. из любого места:

procedure Delete(var head:TSpisok; q:TSpisok); var p:TSpisok; begin

if q=head then head:=q^.next

else begin p:=head;while p^.next<>q do p:=p^.next; p^.next:=q^.next;

end; dispose(q); end;

Списки.Уничтожение списка:

procedure Destroy(head:TSpisok);

var d:TSpisok; begin while head<>nil do begin d:=head^.next;

dispose(head); head:=d; end;

head:=nil; end;

procedure destroy(head:TSpisok);

var d:TSoisok; begin if head<>nil do

begin d:=head^.next; dispose(head);

destroy(d); head:=nil; end; end;

Стек - такой последовательный список с переменной длиной, включение и исключение элементов из которого выполняются только с одной стороны списка, называемого вершиной стека. Применяются и другие названия стека - магазин и очередь, функционирующая по принципу LIFO (Last - In - First- Out - "последним пришел - первым исключается").

Основные операции над стеком - включение нового элемента (английское название push - заталкивать) и исключение элемента из стека (англ. pop - выскакивать).

Полезными могут быть также вспомогательные операции:

· определение текущего числа элементов в стеке;

· очистка стека;

· неразрушающее чтение элемента из вершины стека, которое может быть реализовано, как комбинация основных операций:

x:=pop(stack); push(stack,x).

Для наглядности рассмотрим небольшой пример, демонстрирующий принцип включения элементов в стек и исключения элементов из стека. На рис. 4.1 (а,б,с) изображены состояния стека:

· а). пустого;

· б-г). после последовательного включения в него элементов с именами 'A', 'B', 'C';

· д, е). после последовательного удаления из стека элементов 'C' и 'B';

· ж). после включения в стек элемента 'D'.

Рис 4.1. Включение и исключение элементов из стека.

Очереди с приоритетами

В реальных задачах иногда возникает необходимость в формировании очередей, отличных от FIFO или LIFO. Порядок выборки элементов из таких очередей определяется приоритетами элементов. Приоритет в общем случае может быть представлен числовым значением, которое вычисляется либо на основании значений каких-либо полей элемента, либо на основании внешних факторов. Так, и FIFO, и LIFO-очереди могут трактоваться как приоритетные очереди, в которых приоритет элемента зависит от времени его включения в очередь. При выборке элемента всякий раз выбирается элемент с наибольшим приоритетом.

Очереди с приоритетами могут быть реализованы на линейных списковых структурах - в смежном или связном представлении. Возможны очереди с приоритетным включением - в которых последовательность элементов очереди все время поддерживается упорядоченной, т.е. каждый новый элемент включается на то место в последовательности, которое определяется его приоритетом, а при исключении всегда выбирается элемент из начала. Возможны и очереди с приоритетным исключением - новый элемент включается всегда в конец очереди, а при исключении в очереди ищется (этот поиск может быть только линейным) элемент с максимальным приоритетом и после выборки удаляется из последовательности. И в том, и в другом варианте требуется поиск, а если очередь размещается в статической памяти - еще и перемещение элементов.

Наиболее удобной формой для организации больших очередей с приоритетами является сортировка элементов по убыванию приоритетов частично упорядоченным деревом, рассмотренная нами в п.3.9.2.

Логическая структура дека

Дек - особый вид очереди. Дек (от англ. deq - double ended queue,т.е очередь с двумя концами) - это такой последовательный список, в котором как включение, так и исключение элементов может осуществляться с любого из двух концов списка. Частный случай дека - дек с ограниченным входом и дек с ограниченным выходом. Логическая и физическая структуры дека аналогичны логической и физической структуре кольцевой FIFO-очереди. Однако, применительно к деку целесообразно говорить не о начале и конце, а о левом и правом конце.

Операции над деком:

· включение элемента справа;

· включение элемента слева;

· исключение элемента справа;

· исключение элемента слева;

· определение размера;

· очистка.

Сложение многочлена

коэффициент-k; степень-s; первый многочлен-p; второй многочлен-q; |-стрелочка

begin

q1:=q;

p:=p|.next;

q:=q|.next;

while (p|.k<>0) and (p|.s<>0) do

if p|.s<q|.s

then begin

q1:=q;

q:=q|.next;;

end

else

if p|.s>q|.s

then begin

new(q2);

q2|.k:=p|.k;

q2|.s:=p|.s;

q2|.next:=q;

q1|.next:=q2;

q1:=q2;

p:=p|.next;

end

else begin

q|.k:=q|.k+p|.k;

if q|.k=0

then begin

q2:=q;

q1|.next:=q|.next;

q:=q|.next;

dispose(q2);

end

else begin

q1:=q;

q:=q|.next;

end;

p:=p|.next;

q:=q|.next;

end;

end;

49.1 Дерево-рекурсивная, динамическая структура данных.

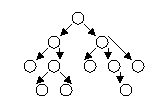Дерево с базовым типом T это либо пустое дерево, любо вершина типа Т с конечным числом связанных с ней деревьев, которые называются поддеревьями.

49.2 Способы изображения деревьев:

Граф – вершины соединяются дугами, согласно их подчинению.

Вложенные множества – любое дерево это множество

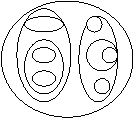
Вложенные скобки - (A, (B, (D), (E, (I), (J))), (C, (K), (M, (P)), (N)))

Отступы

A

B

D

E

I

J

C

K

M

P

N

Корень - самая верхняя вершина дерева.

Корень - вршина не имеющая родителей.

Лист – вершина, не имеющая потомков.

Деревья бывают упорядоченными.

Упорядоченное дерево – дерево, ветви которого упорядоченны по какому-либо признаку

Степень вершины – число поддеревьев, связанных с этой вершиной.(вершины степени 0 носят название концевые, терминальные вершины или листья)

Высота дерева – максимальный путь от корня до листьев дерева

49.3 Способы представления деревьев:

Стандартная форма – в каждой вершине ссылка на всех потомков;

Обратная форма – в каждой вершине ссылка на родительскую(ие) вершины;

Расширенная форма – в каждой вершине хранятся ссылки на потомков и на родителя(ей) этой вершины

49.4 Обход дерева- систематический просмотр всех вершин, при котором каждая вершина встречается один раз.

Прямой

1 попасть в корень

2 пройти левое поддерево

3 пройти правое поддерево

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

Write(root^.inf); 01(root^.left); 01(root^.right);

End;

End.

Обратный

1 пройти левое поддерево

2 попасть в корень

3 пройти правое поддерево

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

01(root^.left); Write(root^.inf); 01(root^.right);

End;

End.

Концевой

1 пройти левое поддерево

2 пройти правое поддерево

3 попасть в корень

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

01(root^.left); 01(root^.right); Write(root^.inf);

End;

End.

50.1 Идеально сбалансированное дерево – дерево, количество вершин в левом и правом поддеревьях которого отличается не более чем на 1.

Построение идеально сбалансированного дерева:

1) расположить 1е число в корне дерева;

2) построить аналитическим методом левое поддерево с кол-ом вершин «n div 2»

3) построить правое поддерево с кол-ом вершин «n - n div 2 – 1»

Function idealtree(n:integer):Ttree;

Var p:Ttree;

Begin

If n=0 then idealtree:=nill;

Else begin

New(p);

Read(p^.inf);

P^.left:=idealtree(n div 2);

P^.right:=idealtree(n - n div 2 - 1);

Idealtree:=p;

End;

End;

50.2

51.1 Алгоритм поиска по дереву с включением:

1.1) 1е значение разместить в корне

1.2) 2е значение сравнивается с тем, что расположено в вершине, если меньше, то вершина левого, если больше, то вершина правого поддерева.

2.1) если новое значение равно, то не выполняется,

2.2) если меньше, то к левому поддереву,

2.3) если больше, то к правому.

Procedure search1(var root:Ttree; x:real);

If root<>nil then begin

New (root);

With root^. Do

Inf:=x;

Left:=nil;

Right:=nil;

End;

Else

If x<root^.inf then search1(root^.left,x)

Else if x>root^.inf then search1(root^.right,x)

Else;

End;

52.1 Ident=record

Name:string;

S:sid

T:ref

Left,right:^Ident;

End;

TIdent=^Ident;

алгоритм идентификации:

1) рассмотреть минимальный блок прикладного вхождения идентификатора, если найдено – процесс завершается,

2) Иначе перейти к блоку, который непосредственно объемлет данный и повторить алгоритм.

Procedure search_ident(x:string;y:sid;z:ref;head:TScope);

Var p:Tscope;

Root:Tident;

Found:Boolean;

Begin

P:=head;

Found:=false;

Repeat

Root :=p^.first_id;

While (root<>nil) and (found=false) do

Begin

If (root^.name=x) and (root^.s:=y) and (root^.t:=z) then

Found:=true;

Else

Begin

If x>root^.name then root:=root^.right

Else if x<root^.name then root:=root^.left

End;

End;

If not found then p:=p^.top_scope;

Until (p=nil) or (found=true)

If not found then error (‘идентификатор не найден’);

End;

Удалить дерево:

procedure delete(var root:tree);

begin

if root<>nil

then begin

delete (root|.left);

delete(root|.right);

dispose(root);

end;

Удалить вершину:

procedure delete_element(var root:tree; x:integer);

var q:tree;

begin

if root<>nil

then

if x<root|.inf

then delete_element(root|.left,x)

else x>root|.inf then delete_element(root|.right,x)

else begin

q:=root;

if q|.right=nil

then root:=q|.left

else if q|.left=nil

then root:=q|.right

else del(q|.left);

dispose(q)

end;

end;

procedure del(var r:tree);

begin

if r|.right<>nil

then del(r|.right)

else begin

q|.inf:=r|.inf;

q:=r;

r:=r|.left;

end;

end;

Сравнение деревьев

function equal(root1,root2:tree):boolean;

begin

if (root1<>nil)and(root2<>nil)

then begin

equal:=(root1|.inf=root2|.inf)

end equal:=(root1|.left=root2|.left)

end equal:=(root1|.right=root2|.right)

else if (root1=nil)and(root2=nil)

then equal:=true

else equal:=false;

end;

Слияние деревьев:

procedure concat(var root1:tree; root2:tree);

begin

if root2<>nil

then begin

search_and_insert(root1,root2|.inf);

concat(root1,root2|.left)

concat(root1,root2|.right)

end;

end;

55.1 АВЛ-дерево — балансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ-деревья названы по первым буквам фамилий их изобретателей Адельсона-Вельского и Ландиса.

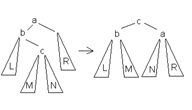
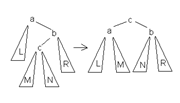
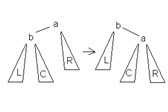
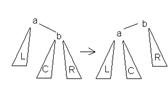
Большое левое вращение(BL) Большое правое вращение(BR) Малое левое вращение(LL) Малое правое вращение(LR)

55.2

Procedure searchavl(var root: avl_tree; x:real;var q:boulean);

Var p2,p1: avl_tree

Begin

If root = nil then

Begin

New(root);

Root^.inf:=x;

Root^.count:=1;

Root^.left:=nil;

Root^.right:=nil;

Root^.bal:=0;

Q:=true;

End;

Else if x<root^.inf then begin

Searchavl (root^.left,x,q);

If q then

Begin

Case root^.bal of

1: begin root^.bal:=0;

Q:=false;

End;

0: begin

Root^.bal:=-1

End;

-1: begin p1:=root^.left;

If p1^.bal=-1 then begin

LL(root,p1);

Root^.bal:=0;

Root:=p1;

End;

Else

Begin

P2:=p1^.left;

LR(root,p1,p2);

If p2^.bal=-1

Then root^.bal:=1;

Else root^.bal:=0;

If p2^.bal=1;

Then p1^.bal:=-1

Else p1^.bal:=0

Root:=p2;

End;

Q:=false;

End;

End;

End;

Else if x>root^.inf then

Begin searchavl(root^.right,x,q);

If q then begin case root^.bal of

-1: begin

root^.bal:=0;

q:=false;

end;

0: root^.bal:=1

1: begin p1:=root^.right;

If p1^.bal=1 then

Begin RR(root;p1);

Root^.bal:=0;

Root:=p1;

End;

Else begin

P2:=p1^.right;

RL(root,p1,p2);

If p2^.bal=1 then

Root^.bal:=1

Else root^.bal:=0

If p2^.bal=-1 then

P1^.bal:=1

Else p1^.bal:=0;

Root:=p2;

End;

Q:=false;

End;

End;

End;

Root^.count:=root^.count+1;

End;

56Сбалансированные деревья(АВЛ-деревья).Дерево называется сбалансированным если высоты его правого и левого деревьев отличны не более чем на 1.

АВЛ-деревья названы по первым буквам фамилий их изобретателей Адельсона-Вельского и Ландиса.

Большое левое вращение(BL) Большое правое вращение(BR) Малое левое вращение(LL) Малое правое вращение(LR)

56.2 procedure deleteavl(var root: avl_tree;x:real;var h:boulean);

var: q:avl_tree;

procedure del (var R:avl_tree; var h:boulean);

begin

if r^.right<>nil then

begin del(r^.right,h)

end;

if h then balanceR(r,h)

else

begin

q^.inf:=r^.inf;

q^.count:=r^.count;

q:=r;

r:=r^.left;

h:=true;

end;

end;

begin

if root=nil then write (‘дерева нет’);

else if x<root^.inf then

begin

deleteavl(root^.left;x;h);

if h then balanceL(root;h);

end;

else if x > root^.inf then

begin

deleteavl(root^.right;x;h);

if h then balanceR(root;h);

end;

else

begin

q:=root;

if q^.right=nil then

begin

root:=q^.left;

h:=true;

end;

else if q^.left=nil then

begin

root:=q^.right;

h:=true;

end;

else begin

del(q^.left;h);

if h then balanceL(root;h);

end;

dispose(q);

end;

end;

procedure balanceL(var root:avl_tree;var h:boulean);

var p1,p2:a