Интерполяция и аппроксимация функций
Постановка задачи
В дискретные моменты времени х1, х2, …, хn были проведены измерения некоторой физической величины Y. Результаты эксперимента представлены в таблице.
Таблица
| Х | |||||
| Y |
Требуется определить значения физической величины на всем временном интервале x1<=x<=xn.
Задача определения значений физической величины на всем временном интервале сводится к задаче о приближении функции Y(x). Заданную таблицей функцию Y(x) заменим на функцию f(x; a1, …,an) таким образом, чтобы отклонение функции Y(x) от приближающей функции f(x; a1, …,an) на указанном множестве х1, х2, …, хn было наименьшим. При этом функция f(x; a1, …,an) в общем случае называется аппроксимирующей функцией. Если параметры a1, …,an определяются из условия совпадения функции Y(x) и приближающей функции в точках х1, х2, …, хn , т.е. из условия равенства f(xi; a1, …,an)=Y(xi), то такую функцию f(xi; a1, …,an) называют интерполирующей.
Рассмотрим случаи линейной, квадратичной интерполяции и общий случай интерполирования полином Qm(x)=a0+a1x+…+amxm степени m, а также выполним аппроксимацию заданной экспериментальной зависимости полиномом 1-ой степени.
Для решения задачи будем использовать возможности, предоставляемые электронными таблицами Microsoft Excel. Перенесем исходную таблицу экспериментальных данных в рабочий лист книги Microsoft Excel для определенности располагая в ячейках A3:F4 (см. рис. 11).
Линейная интерполяция.
В случае линейного интерполирования искомая функция f(x) представляет собой ломаную линию. Уравнения каждого отрезка ломаной определяются из условия прохождения прямой через данную соседнюю пару точек. Например, неизвестные коэффициенты а0, а1 уравнения прямой y=a0+a1*x, проходящей через первую и вторую точки, могут быть найдены из системы линейных уравнений:
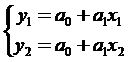 |
Первое уравнение системы - это условие прохождения прямой через точку с координатами (x1,y1), второе уравнение - условие прохождения прямой через точку с координатами (x2,y2). Таким образом, задача нахождения искомой функции, описывающей заданную табличную зависимость в случае линейного интерполирования сводиться к нахождению уравнений прямых, соединяющих точки 1 и 2, 2 и 3, 3 и 4, 4 и 5 соответственно.
Выполним линейную интерполяцию средствами электронных таблиц Excel. Для этого вначале построим график заданной экспериментальной зависимости. Для этого будем использовать Мастер диаграмм (см. кнопка Мастера диаграмм на панели инструментов Стандартная или пункт меню Вставка - Диаграмма). Экспериментальные данные будем отображать точками, для этого на первом шаге Мастера диаграмм необходимо выбрать точечный тип диаграммы и нажать на кнопку <Далее>. На втором шаге Мастера диаграмм необходимо перейти на вкладку Ряд и добавить ряды данных, по которым будет строиться диаграмма. Для этого необходимо нажать на кнопку <Добавить> и затем ввести значения Х и Y, соответствующие данному ряду значений. В случае линейной интерполяции мы имеем четыре ряда данных: Ряд1 формируется из координат точек 1 и 2, Ряд2 - из координат точек 2 и 3, Ряд3 - из координат точек 3 и 4, Ряд4 - из координат точек 4 и 5. Рассмотрим более подробно формирование Ряда 1. Диапазон значений Х и Y (ячейки, содержащие координаты х и у точек 1 и 2) может быть указан с помощью манипулятора мышь путем простого выделения соответствующего диапазона ячеек (если окно Мастера диаграмм загораживает необходимый диапазон ячеек, его можно отбуксировать, уцепившись "мышью" за заголовок окна). Результат представлен на рис.9. Проверьте, Ряд 1 имеет Значения Х - =Лист1!$B$3:$C$3, Значения Y - =Лист1!$B$4:$C$4.
Для того, чтобы начать формирование Ряда 2 необходимо нажать на кнопку Добавить. Значения Х и Y Ряда 2 - это диапазон ячеек с координатами x и y точек 2 и 3 (Значения Х – =Лист1!$C$3:$D$3, Значения Y - =Лист1!$C$4:$D$4). Аналогично формируются Ряды 3 и 4.
Сформировав ряды данных необходимо нажать на кнопку <Далее>. В третьем окне Мастера диаграмм необходимо указать название диаграммы и осей, во вкладке Легенда снять флажок Добавить легенду и нажать на кнопку <Готово>. На рабочем листе должна появиться диаграмма, отображающая заданную табличную зависимость.
Далее для выполнения линейного интерполирования по заданным точкам необходимо выполнить Меню Диаграмма - Добавить линию тренда. Пункт Диаграмма присутствует в меню Microsoft Excel, если построенная диаграмма выделена - вокруг области диаграммы должна быть черная рамка, если ее нет - по области диаграммы необходимо щелкнуть левой кнопкой мышки. В появившемся окне Линия тренда во вкладке Тип необходимо выбрать Линейная,
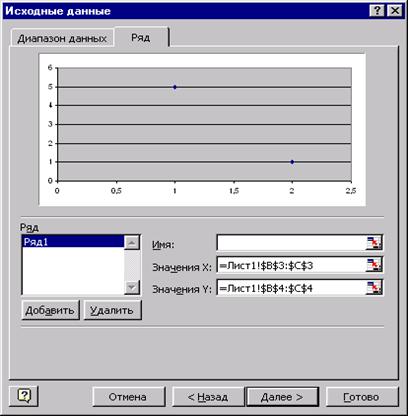
Рис. 9
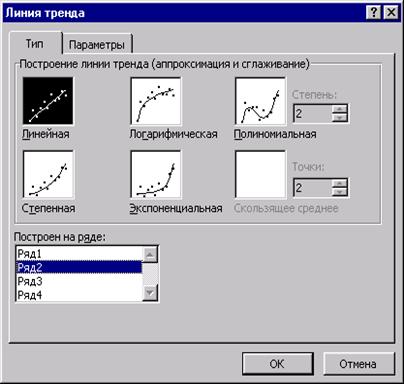
Рис. 10
затем перейти на вкладку Параметры и установить флажок Показывать уравнение на диаграмме и нажать <ОК>. В результате на диаграмме должна появиться прямая линия, соединяющая точки 1 и 2 и ее уравнение. Далее необходимо снова выполнить Меню Диаграмма - Добавить линию тренда, во вкладке Тип в окошке Построен на ряде необходимо щелкнуть мышкой по Ряд2 (см. рис. 10) и проделать все вышеописанные действия. В результате на диаграмме должна появиться прямая, соединяющая точки 2 и 3 и ее уравнение.
Аналогично нужно построить линейный тренд, используя Ряд3 и Ряд4 данных. Результат представлен на рис. 11.
Квадратичная интерполяция
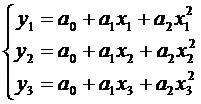 |
В случае квадратичной интерполяции исходная функция заменяется отрезками параболы, проходящих через три соседних точки. Неизвестные коэффициенты а0, а1, а3 в уравнении параболы y=a0+a1*x+a2*x2, проходящей через точки с координатами (x1,y1), (x2,y2) и (x3,y3) может быть найдено из системы уравнений:
Выполним квадратичное интерполирование заданной табличной зависимости, используя возможности электронных таблиц Excel. Для этого необходимо снова построить график экспериментальной зависимости, выбрав точечный тип диаграммы. Последовательность построения графика аналогична приведенной для случая линейного интерполирования, только в рассматриваемом случае необходимо сформировать только 2 ряда данных. Ряд1 формируется из координат точек 1, 2, 3; Ряд2 формируется из координат точек 3, 4, 5. (Проверьте, Ряд1 - Значения Х - = Лист1!$B$3:$D$3, Значения Y - =Лист1!$B$4:$D$4; Ряд2 - Значения Х - = Лист1!$D$3:$F$3, Значения Y - =Лист1!$D$4:$F$4).
Далее для выполнения квадратичного интерполирования по заданным точкам необходимо выполнить Меню Диаграмма - Добавить линию тренда. В появившемся окне Линия тренда во вкладке Тип необходимо выбрать Полиномиальная, Степень 2; затем перейти на вкладку Параметры и установить флажок Показывать уравнение на диаграмме и нажать <ОК>. В результате на диаграмме должна появиться парабола, соединяющая точки 1, 2 и 3 и ее уравнение. Затем необходимо снова выполнить Меню Диаграмма - Добавить линию тренда, во вкладке Тип в окошке Построен на ряде необходимо щелкнуть мышкой по Ряд2 и проделать все действия, описанные выше. В результате на диаграмме должна появиться еще одна парабола, построенная на точках 3, 4 и 5 и ее уравнение. Результат представлен на рис.11.
