По заданному расположению корней

Цель работы

1. Определение коэффициентов обратной связи, обеспечивающее заданное расположение корней характеристического уравнения замкнутой системы и, следовательно, заданный вид переходного процесса.

2. Определение для многомерного объекта коэффициентов обратной связи, обеспечивающее заданное расположение корней характеристического уравнения замкнутой системы и заданный вид переходного процесса.

Теоретическое обоснование

В координатах пространства состояний поведение линейной системы описывается следующими матричными уравнениями:

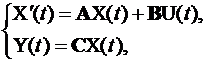(10.1)

где А – матрица коэффициентов состояния; В – матрица коэффициентов управления; С – матрица коэффициентов наблюдения системы.

Если известна передаточная функция системы

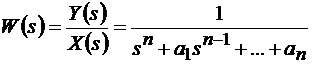, (10.2)

то матрицы А и В записывается в следующем виде

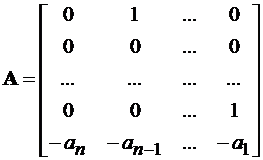; . (10.3)

Такое представление матриц называется каноническим.

Качество переходного процесса определяется корнями характеристичес-кого уравнения замкнутой системы.

Одним из вариантов оптимального переходного процесса является обеспечение одинаковости всех корней характеристического уравнения, причем, корни должны быть действительными и отрицательными со значением модуля w₀. Тогда характеристическое уравнение замкнутой системы обращается в бином Ньютона (s + w₀)ⁿ. Другим вариантом является предложенное Баттервортом расположение корней по окружности радиуса w₀ в левой полуплоскости комплексной плоскости.

Можно задавать корни характеристического уравнения замкнутой системы и по ним получить желаемую передаточную функцию

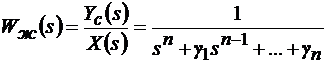(10.4)

для которой записана желаемая матрица состояния А_ж:

. (10.5)

Матрица состояния А и желаемая матрица состояния А_ж должны быть записаны в одном и том же каноническом базисе.

Доказано, что стационарная система 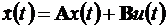с характеристи-ческим многочленом sⁿ + a₁s^n-1 +…+ a_n может быть приведена к желаемой системе 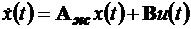с желаемым характеристическим многочленом sⁿ + γ₁s^n-1 +…+ γ_n, сформированным путем выбора коэффициентов K обратной связи.

Так как матрицы А и А_ж записаны в одном базисе, то можно записать в уравнение, позволяющее определять коэффициенты обратной связи K

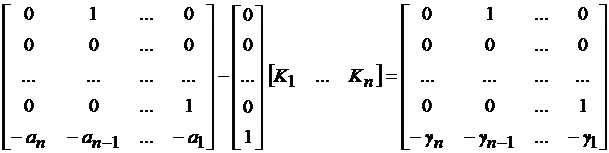.(10.6)

Решение матричного уравнения (10.6) позволяет определить неизвестные коэффициенты обратной связи K₁, …, K_n

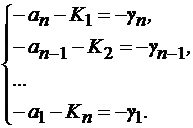(10.7)

Из уравнения (10.7) составляющие вектора K равны

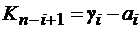. (10.8)

Определение коэффициентов обратных связей возможно с помощью матричных передаточных функций. Для этого выражению (10.1) необходимо применить преобразование Лапласа

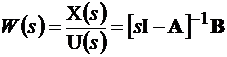. (10.9)

После преобразования матриц А и В матричную передаточную можно получить в виде

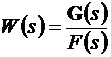. (10.10)

где G(s) - матрица-столбец, а 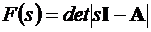– характеристический поли-ном объекта располагаемой системы.

Структурная схема замкнутой системы, образуемая в результате присоединения к объекту (рис. 10.1) САУ (рис. 10.2) (матрицы коэффициен-тов обратных связей K), приведена на рис. 10.3.

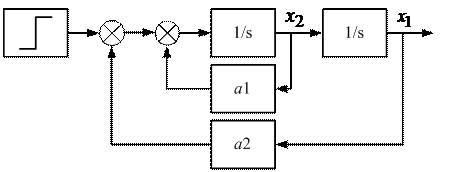
Рис. 10.1. Cтруктурная схема исходной системы

Характеристическое уравнение замкнутой системы получено суммиро-ванием передаточной функции разомкнутой системы с единицей

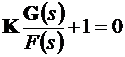или K×G(s) + F(s) = 0. (10.11)

Считая полином H(s) желаемым характеристическим полиномом замкнутой системы, получаем

K×G(s) = H(s) – F(s). (10.12)

В этом выражении неизвестной является только матрица-строка K.

Матрица-столбец G(s) вместе с полиномами F(s) и H(s) определены соответственно параметрами объекта и желаемым расположением корней характеристического уравнения замкнутой системы. Приравнивая коэффици-енты левой и правой частей (10.12) при одинаковых степенях s, получаем систему алгебраических уравнений, из которой можно найти все элементы матрицы регулятора K.

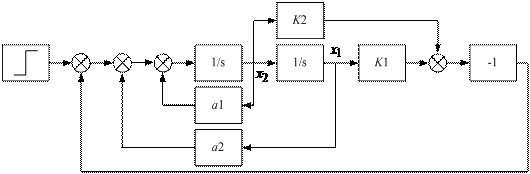
Рис. 10.2. Структурная схема скорректированной системы

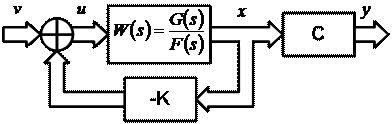
Рис. 10.3 Структурная схема замкнутой системы

Синтез САУ многомерных объектов

Для многомерного объекта матрица управления В имеет больше одного столбца. Задача управления состоит в нахождении такой ( 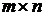) - матрицы K-регулятора, при которой замкнутая многомерная система получает наперед заданное расположение корней.

Характеристическое уравнение замкнутой системы, структурная схема которой изображена на рис.10.4, имеет вид

det(sI + BK) = 0. (10.13)

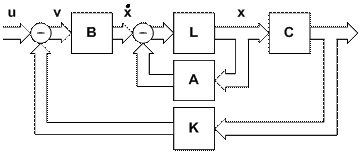
Рис. 10.4 . Структурная схема системы с многомерным регулятоpом

Задачу синтеза многомерного регулятора (регулятора с несколькими выходами) можно свести к рассмотрению одномерной задачи (регулятора с одним выходом). Для этого K-матрицу ( 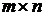) представляют в виде

K = QL,

где Q – матрица-столбец ( 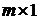), а L – матрица-строка ( 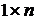), C – единичная матрица.

Тогда уравнение (10.13) можно переписать

det(sI – A + BQL).

Введем обозначения BQ = b и получим

det(sI – A + bL). (10.14)

Замена BQ = b позволяет заменить многомерный регулятор (матрица B), представленный в виде произведения двух одномерных матриц – матрицы регулятора L ( 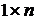) и матрицы Q ( 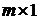), одномерным регулятором (матрица b). Преобразованная структурная схема приведена на рис. 10.5.

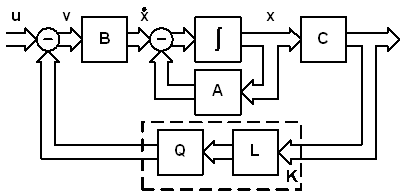
Рис. 10.5. Преобразованная структурная схема замкнутой многомерной системы

Корни характеристического уравнения с многомерным регулятором (рис. 10.4) совпадают с корнями характеристического уравнения с одномер-ным регулятором (рис. 10.5), поэтому синтез многомерного регулятора может быть выполнен по следующей методике:

1. Выбирают матрицу Q размером 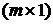( 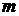– число строк матрицы управления). Матрица Q преобразует входной сигнал размерности ( 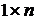) в выходной сигнал размерности ( 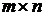). Матрица Q определяет глубину обратной связи по компонентам матрицы. Например, если 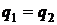, то влияние обратных связей по входу один и два одинакова, а если 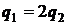, то обратная связь по входу один в 2 раза глубже, чем обратная связь по входу два.

2. При выбранной матрице Q и известной матрице B можно из уравнения (10.14) определить матрицу L одномерного объекта, обеспечиваю-щее желаемое расположение корней замкнутой системы.

3. Матрицу многомерного регулятора для многомерного объекта определяем согласно выражению

K = QL. (10.15)

Описание работы

Определим коэффициенты обратной связи для системы регулирования, передаточная функция которой задана уравнением

.

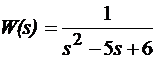Для этого с помощью пакета Simulink построим модель и сохраним ее под именем «mod10_1» (рис. 10.6)

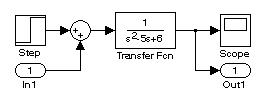
Рис. 10.6. Модель звена

Используя передаточную функцию определим матрицу состояния, соответствующую выбранной системе

[A,B,C,D]=linmod('mod10_1'), откуда

, , , .

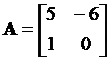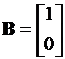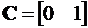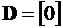Желаемая матрица состояния определяется заданным расположением корней характеристического уравнения замкнутой системы

; ; .

.

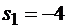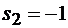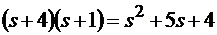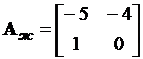Подставляя значение матриц А и А_ж в (10.6), получаем А – B × K = А_ж или

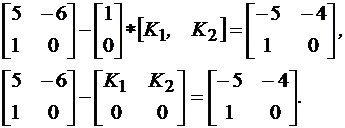(10.16)

Из уравнения (10.13) получим соотношения

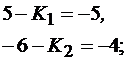
решение которых позволяет получить значения обратных связей , .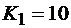

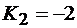Предыдущий пример можно решить, используя понятие передаточной функции. Передаточная функция разомкнутой системы имеет вид

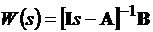
F=inv([Is]-[A])

W=F*B

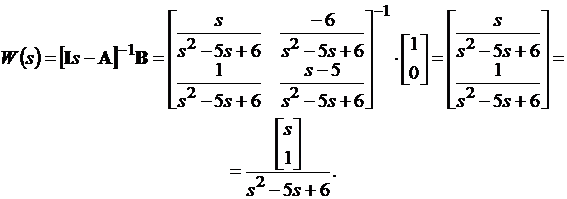
С учетом матрицы регулятора K и желаемого характеристического уравнения 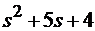получаем соотношение

.

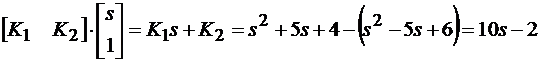Из последнего выражения находим, что , .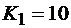

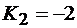Рассмотренную задачу, определения вектора K коэффициентов обрат-ных связей, можно решить в пакете MatLab с помощью команд acker и place.

Приведем решение вышеприведенной задачи. Известны матрицы A и B. Матрицей P задаём желаемое расположение полюсов замкнутой системы.

A=[5,-6;1,0] %Матрица коэффициентов состояния А

B=[1;0] %Матрица коэффициентов управления B

P=[-4;-1] %Задание полюсов замкнутой системы

K1=acker(A,B,P) %Определение коэффициентов обратной связи

K2=place(A,B,P) %Определение коэффициентов обратной связи.

MatLab определят коэффициенты матрицы K: K₁ = 10, K₂ = –2.

Функция acker применима только для одномерных систем.

Функция place имеет более широкие возможности и рассчитывает матрицу K коэффициентов обратных связей, как для одномерных, так и для многомерных систем.

В пакете MatLab, поставленную задачу также можно решить, используя формулу Аккермана.

A=[5,-6;1,0] %Матрица коэффициентов состояния А

B=[1;0] %Матрица коэффициентов управления B

Ak=A*B %Определение составляющих

Ak1=[B,Ak] %формулы Аккермана

Ak2=inv(Ak1) %Определение обратной матрицы.

I=[1,0;0,1] %Ввод единичной матрицы.

syms w a1 a2 %Ввод символьных переменных

a1=1 %Ввод чисел, определяющих

a2=4 %характеристическое уравнение

w=A^2+(a1+a2)*A+a1*a2*I %Определение матричного полинома

k=[0,1]*Ak2*w %Определение матрицы коэффициентов

%обратных связей формулой Аккермана.

Применим изложенную методику при решении примера.

Матричные уравнения нескорректированного многомерного объекта:

,

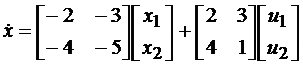где , .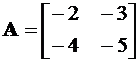

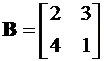Требуется определить многомерный регулятор, обеспечивающий заданное расположение корней замкнутой системы.

Введем матрицу Q, обеспечивающую относительную глубину обратных связей q₁ = 2q₂ = q , и матрицу L

.

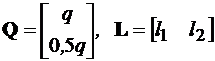Определим передаточную функцию эквивалентной одномерной системы W(s) = (sI – A)^-1BQ.

F=inv([Is]-[A])

W=F*B*Q.

.

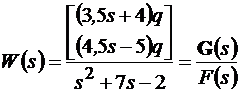Корни характеристического уравнения синтезируемой замкнутой систе-мы расположены в точках s₁ = –7; s₂ = –9. Так как желаемый характерис-тический многочлен известен

,

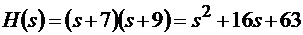то условие для определения матрицы В

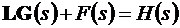, (10.17)

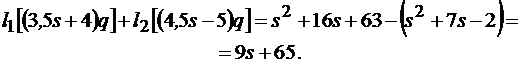(10.18)

где l₁ и l₂ -компоненты матрицы L.

Приравнивая составляющие уравнения (10.18) при одинаковых степенях 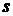, получим

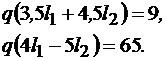(10.19)

Решение системы уравнений (10.19) позволяет определить l₁ и l₂

, .

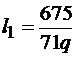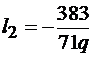Подставляя значение матриц Q и L в уравнение (10.15), получим матрицу двумерного регулятора

.

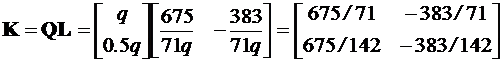С учетом q₁ = 1, q₂ = 0,5 можно изобразить структурную схему скорректированной системы, которая приведена на pис.10.7.

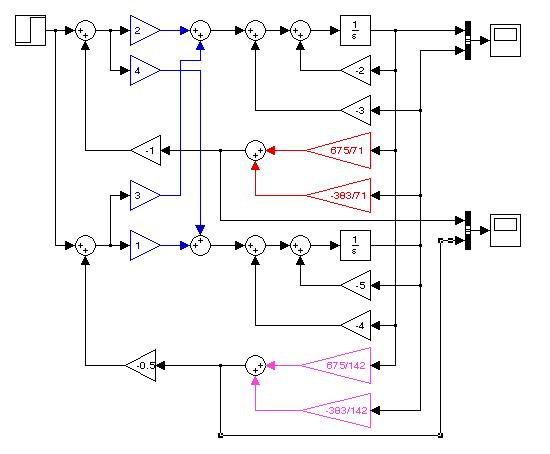
Рис. 10.7.Структурная схема системы с регулятором,

синтезированным методикой приведения многомерного регулятора к одномерному

По приведенной методике синтезируются переходные характеристики не по фазовым координатам системы, а по выходным координатам матрицы L. На рис. 10.8 приведены результаты моделирования скорректированной системы: а) параметры состояния x₁, x₂; б) выходные координаты матрицы L. При этом переходные процессы по фазовым координатам 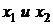не отвечают заданному расположению корней замкнутой системы, а заданным требованиям отвечают выходные координаты матрицы L.

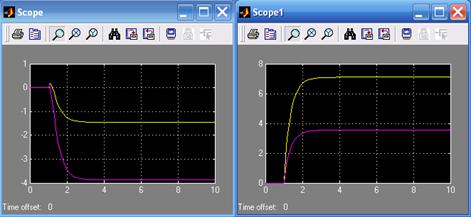
a) б)

Рис. 10.8. Результаты моделирования скорректированной системы

Поэтому синтез регулятора целесообразно выполнить в пакете MatLab командой place.

A=[-2,-3;-4,-5] %Задание матрицы коэффициентов состояния А системы

B=[2,3;4,1], %Задание матрицы коэффициентов управления B системы

P=[-7,-9]; %Вектор полюсов замкнутой системы

K=place(A,B,P) %Определение коэффициентов обратной связи.

В результате получена матрица многомерного регулятора

.

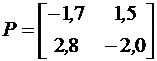Результаты моделирования оптимального управления представлены на рис. 10.9. Результаты моделирования структурной схемы с многомерным регулятором показывают, что переходные процессы по фазовым координатам соответствуют расположению корней характеристического уравнения замкнутой системы.

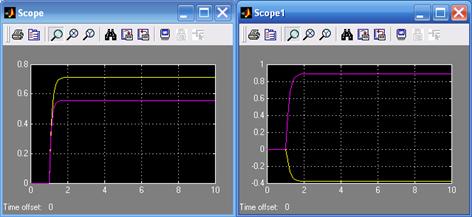
a) б)

Рис. 10.9. Результаты моделирования скорректированной системы с помощью команды place

На рис. 10.10 приведена структурная схема системы, синтезированная с помощью команды place.

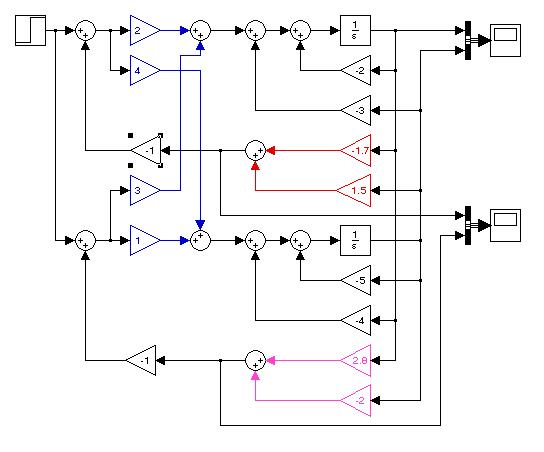
Рис. 10.10.Структурная схема системы с регулятором,

параметры которого определены командой place.

Задание

1. Исходя из заданного расположения корней характеристического уравнения замкнутой системы (табл. 1) определить коэффициенты обратной связи (параметры одномерного регулятора).

2. Составить структурные схемы системы (рис. 10.2) и системы с одномерным регулятором (рис. 10.3).

3. По заданному матричному уравнению исходной системы (табл. 2), заданной глубине обратных связей и корням характеристического уравнения желаемой системы определить параметры многомерного регулятора.

4. С учетом рассчитанных параметров многомерного регулятора составить структурную схему.

5. По заданному матричному уравнению исходной системы (табл. 2) и корням характеристического уравнения желаемой системы определить в пакете Control System Toolbox параметры многомерного регулятора.

6. С учетом параметров многомерного регулятора, определенного в пакете Control System Toolbox, составить структурную схему.

Содержание отчета

1. Расчет коэффициентов обратных связей для двух значений корней скорректированной системы с одномерным регулятором. Коэффициенты обратных связей определяют тремя методами:

- через матричные соотношения;

- через характеристическое уравнение замкнутой системы;

- через задание корней в пакете MatLab.

2. Структурная схема исходной системы и системы с одномерным регулятором.

3. Реакция исходной системы и системы с одномерным регулятором на ступенчатое воздействие.

4. Расчет параметров многомерного регулятора.

5. Структурная схема системы с многомерным регулятором.

6. Реакция системы с многомерным регулятором на ступенчатое воздействие.

7. Структурная схема с многомерным регулятором, параметры которого были определены в пакете Control System Toolbox.

8. Реакция системы с многомерным регулятором, параметры которого были определены в пакете Control System Toolbox, на ступенчатое воздейст-вие.

9. Анализ результатов моделирования и выводы.

Контpольные вопpосы

1. Как записать матрицу управления A по известной передаточной функции замкнутой системы?

2. Как по корням характеристического уравнения замкнутой системы получить передаточную функцию?

3. Как по корням характеристического уравнения замкнутой системы получить матрицу состояния?

4. Опишите методику определения коэффициентов обратной связи, используя матричные передаточные функции.

5. Какие функции используются в MatLab для определения коэффициентов обратной связей одномерных и многомерных систем.

6. Опишите методику определения параметров многомерного регулятора.

7. Какие объекты называются многомерными и приведите их примеры.

8. Какие исходные данные требуются для выполнения команды place.

9. Изменятся ли переходные характеристики системы, если поменять относительную глубину обратных связей.

10. В чем различие методик, по которым определены параметры многомерного регулятора, представленные на рис. 10.7 и рис. 10.10.

Лабораторная работа № 11