Тема: ПОЛУЧЕНИЕ КОЭФФИЦИЕНТОВ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ И ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ

Цель работы. Получение навыков построения линейной модели для множественной зависимости по данным экспериментов.

Краткие сведения из теории

Множественной регрессией называется взаимосвязь трех и более переменных, или влияние двух и более аргументов на функцию

.

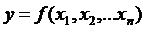Для простоты рассмотрим случай, когда ищется зависимость y от двух аргументов x ₁ и x ₂ . Такую зависимость графически можно представить в трехмерном пространстве {у, x ₁ , x ₂} Совокупность всех т точек представляет собой корреляционное пространство. Задача определения зависимости у от x₁ и x₂ состоит в том, чтобы подобрать такую плоскость, которая наилучшим, в смысле принципа наименьших квадратов, образом вписалась бы в данное корреляционное пространство. Зависимость ищется в виде:

.

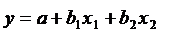Расстояние от точек корреляционного пространства до плоскости определяется выражением:

.

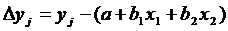Требуется найти значения коэффициентов a, b ₁ и b ₂.

Продифференцировав функцию суммы квадратов отклонений по коэффициентам a, b₁ и b₂ и приравняв производные к нулю, получим систему трех уравнений с тремя неизвестными:

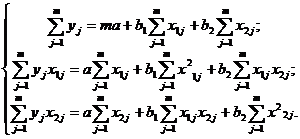(4.1)

Решение системы уравнений относительно коэффициентов a, b₁ и b₂, позволяет определить их численные значения. Величины Sy,Sx₁, Sx₁², S yx₁, Sy x₂, Sx₂, Sx₂², Sx₁ x₂ ^.находятся непосредственно по данным измерений.

Таким образом, найденное уравнение регрессии описывает совместное влияние x ₁ и x₂ на функцию у. Коэффициенты a, b₁ и b₂ при этом имеют следующий математический смысл.

Коэффициент а равен значению функции у при нулевых значениях аргументов x₁ и x₂. В геометрической интерпретации он соответствует ординате точки пересечения плоскости регрессии с осью y.

Коэффициент b₁ равен изменению функции у при изменении первого аргумента х₁ на единицу при неизменном втором аргументе x₂. Аналогично, коэффициент регрессии b₂ равен изменению функции у при изменении второго аргумента x ₂ на единицу при неизменном первом аргументе x ₁.

Из уравнения множественной линейной регрессии могут быть получены уравнения частной регрессии аргументов x₁ и x₂ на функцию у:

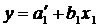; ( 4.2 )

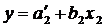. ( 4.3 )

При этом угловые коэффициенты регрессии b ₁ и b ₂ сохраняют те же числовые значения, что и в уравнении множественной регрессии. Свободные члены уравнений для yможно подсчитать следующим образом:

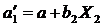; ( 4.4 )

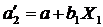. ( 4.5 )

где а— свободный член в уравнении множественной регрессии ;

X _1, X ₂—средние значения соответствующих аргументов.

Оценкой тесноты связи при множественной линейной регрессии служит коэффициент множественной корреляции R, определяемый по формуле:

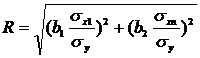. (4.6)

Величина коэффициента множественной корреляции всегда положительна и может меняться от 0 (при отсутствии связи) до 1 (при функциональной связи). С помощью коэффициента множественной корреляции оценивают совместное влияние на зависимую переменную всех включенных в расчет аргументов.

Задание

Решив систему уравнений (4.1), получить в аналитической форме, вычислить значения коэффициентов множественной линейной регрессии, получить с помощью формул (4.2) – (4.5) уравнения частной регрессии, вычислить по формуле (4.6) коэффициент множественной корреляции для заданных рядов данных экспериментов. Построить трехмерные графики корреляционного поля и полученной плоскости, соответствующей уравнению множественной линейной регрессии.

Матрица значений x₁ задается следующим образом:

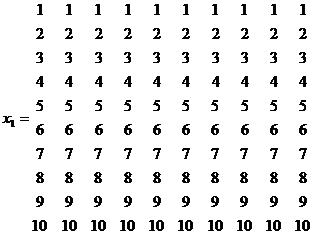
Матрица значений x₂:

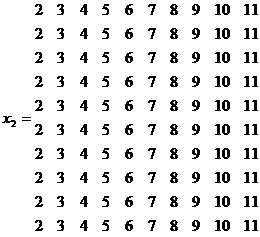
Варианты матрицы y.

Вариант 1

3.7 –3.3 –6.9 –14.5 –19.7 –26.1 –32.7 –37.7 –43.7 –46.5

3.0 –2.8 –6.2 –9.2 –18.2 –26.8 –33.0 –38.4 –41.4 –49.2

3.3 –2.5 0.1 –10.5 –19.3 –20.9 –30.3 –34.9 –39.5 –50.7

5.2 3.4 –9.6 –4.2 –22.0 –14.2 –25.6 –26.6 –39.6 –46.2

1.9 5.1 –8.7 –14.5 –22.3 –19.1 –22.9 –23.7 –27.5 –48.3

22.2 –2.8 –6.2 –8.4 –22.6 –21.2 –25.8 –20.8 –45.8 –49.2

1.7 –1.3 8.3 –3.1 –21.5 –17.5 –28.9 –30.5 –39.1 –49.1

14.4 –2.6 1.2 –4.6 –12.0 –14.6 –23.6 –23.0 –46.4 –33.0

28.5 1.1 16.9 –15.9 –18.1 –0.5 –15.3 –33.7 –21.5 –30.9

13.4 3.6 23.8 14.0 –13.8 2.4 –17.4 –35.2 –21.0 –40.8

Вариант 2

–31.2 –36.2 –43.2 –45.6 –53.4 –56.6 –63.6 –67.6 –73.6 –80.4

–43.3 –48.7 –52.5 –59.5 –65.3 –73.1 –73.3 –84.3 –87.3 –90.7

–57.6 –63.6 –72.0 –72.0 –74.4 –80.4 –87.0 –93.6 –101.4 –100.2

–72.3 –80.1 –80.7 –81.3 –93.1 –100.9 –100.7 –112.5 –115.5 –116.9

–74.8 –86.2 –91.6 –93.0 –101.4 –114.8 –121.2 –124.6 –121.0 –125.4

–82.5 –102.3 –98.1 –119.1 –104.1 –131.1 –135.3 –132.3 –135.3 –152.7

–112.8 –100.0 –123.6 –126.2 –124.6 –127.2 –138.2 –153.4 –161.6 –154.4

–132.7 –136.5 –141.9 –136.1 –131.9 –142.1 –160.3 –146.5 –147.1 –173.3

–118.2 –147.0 –138.0 –152.4 –163.2 –159.6 –172.2 –170.4 –157.8 –190.2

–129.3 –158.7 –154.1 –169.5 –180.9 –176.3 –189.7 –185.1 –198.5 –187.9

Вариант 3

–1.6 7.0 14.4 20.8 25.6 32.6 40.2 49.8 56.8 60.2

–7.6 2.6 5.2 16.2 22.4 29.0 33.6 42.2 50.4 57.8

–12.8 –2.8 –1.8 9.4 14.6 22.8 28.6 32.6 42.6 50.2

–9.6 –13.8 –0.4 1.0 16.8 19.0 26.0 29.8 40.0 39.8

–24.0 –21.0 –14.0 3.0 15.0 16.0 28.0 34.0 38.0 46.0

–17.6 –17.8 –3.6 –9.8 2.0 16.2 26.8 29.0 21.6 37.0

–39.4 –11.4 –29.6 –4.4 –15.6 –0.2 12.4 19.4 27.8 32.0

–36.0 –32.2 –33.2 –21.4 –16.0 0.6 12.4 –1.4 5.6 27.0

–32.0 –43.0 –27.0 –20.0 –29.2 –11.4 17.2 20.6 9.6 22.0

–64.0 –49.0 –34.0 –9.0 –8.0 1.0 –8.0 9.0 10.0 25.0

Вариант 4

9.7 15.1 17.5 21.5 24.7 26.7 30.1 33.5 37.9 40.9

23.2 23.4 31.2 31.4 38.0 37.0 42.0 44.2 46.4 51.8

35.1 38.5 37.1 37.5 39.7 46.1 52.5 48.7 58.1 63.9

36.6 40.8 45.8 50.8 52.6 56.0 56.2 57.2 60.6 76.0

45.3 45.7 53.1 68.5 59.9 72.3 66.7 69.1 67.5 72.9

58.8 63.4 56.0 58.2 65.2 77.0 81.6 79.0 92.0 90.6

72.5 61.9 66.7 67.3 81.9 79.7 88.7 90.7 82.9 98.9

76.2 66.8 84.6 86.4 105.8 91.6 103.0 98.4 105.0 106.8

87.3 90.7 101.3 90.3 115.3 102.5 107.7 94.9 116.3 130.5

88.8 86.2 121.6 123.0 96.4 115.8 113.2 102.6 140.0 123.4

Вариант 5

–23.1 –31.1 –39.3 –45.7 –51.7 –62.9 –67.5 –77.7 –83.5 –90.7

–32.7 –41.3 –49.1 –57.7 –59.5 –67.7 –80.3 –87.7 –95.9 –98.9

–44.9 –53.3 –53.9 –64.7 –71.9 –82.1 –86.9 –97.1 –107.3 –110.3

–44.3 –56.9 –68.7 –66.9 –76.3 –84.9 –91.9 –106.9 –107.5 –112.9

–52.1 –65.9 –64.7 –81.5 –97.3 –90.1 –99.9 –111.7 –126.5 –124.3

–70.7 –74.9 –79.1 –98.9 –101.9 –98.9 –110.3 –124.1 –125.9 –148.1

–78.9 –72.7 –93.1 –100.9 –104.5 –115.1 –121.5 –140.5 –137.1 –151.9

–85.1 –100.9 –107.1 –121.3 –117.9 –124.1 –141.5 –130.1 –157.1 –163.3

–85.1 –107.3 –115.1 –115.7 –134.3 –143.9 –153.5 –139.7 –165.5 –166.1

–109.1 –102.9 –130.7 –144.5 –130.3 –146.1 –135.9 –139.7 –155.5 –181.3

Вариант 6

–5.4 –4.0 –5.6 –4.6 –5.8 –6.0 –5.0 –6.4 –8.2 –7.6

3.6 2.2 8.0 1.4 3.6 6.6 3.6 2.2 7.6 4.6

17.8 17.6 17.4 11.2 11.6 12.0 11.2 19.4 12.0 11.2

21.2 30.6 23.2 34.2 20.4 29.0 21.6 25.4 32.4 18.6

43.6 33.4 38.2 32.0 37.8 44.6 28.4 28.2 37.0 36.8

49.6 49.4 39.6 43.0 44.0 52.2 41.2 37.4 44.4 39.4

57.8 64.6 47.6 65.6 51.4 48.4 49.6 67.6 53.4 51.8

82.8 71.4 66.4 74.2 69.2 78.6 57.6 79.8 76.4 66.6

88.0 69.8 96.6 76.6 89.0 65.4 74.2 81.2 75.6 80.8

75.6 101.4 83.2 107.0 88.8 90.6 100.4 90.2 86.0 81.8