Общие указания по выполнению контрольных заданий

СОДЕРЖАНИЕ

Введение
1 Линейный парный регрессионный анализ
2 Множественный регрессионный анализ
3 Временные ряды в эконометрических исследованиях
Приложение Г Распределение Стьюдента (t-распределение)
Приложение Д Распределение Фишера (F-распределение)

ВВЕДЕНИЕ

Сегодня деятельность в любой области экономики (управления, финансово-кредитной сфере, маркетинге, учете и аудите) требует от специалистов применения современных методов работы, знания достижения мировой экономической мысли, понимания научного языка.

Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний эконометрики научиться их использовать невозможно. Поэтому эконометрика (наряду с микроэкономикой и макроэкономикой) входит в число базовых дисциплин современного экономического образования.

Первая часть методических указаний содержит теоретические аспекты и подробный анализ типовых эконометрических задач. Вторая часть предполагает самостоятельную работу студентов по решению задач. Следует отметить, что условия задач в основном базируются на реальной экономической информации.

ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ

Контрольная работа по курсу выполняется для приобретения студентами опыта построения эконометрических моделей, принятия решений спецификации и идентифика­ции моделей, выбора методов оценки параметров модели, интерпретации результатов, получения прогнозных оценок.

При выполнении контрольных работ следует обратить внимание на следующие требования:

1 Расчеты можно выполнять с использованием статистических возможностей, например, электронных таблиц MS Excel для Windows, либо других статистических или эконометрических пакетов.

2 Нельзя ограничиваться приведением только готовых ответов. Расчеты должны быть представлены в развернутом виде, применяя, где это необходимо табличные оформления исходной информации и расчетов, со всеми формулами, пояснениями и вы­водами, соблюдая достаточную точность вычислений. В пояснениях и выводах показать, что именно и как характеризует исчис­ленный показатель.

5 Работа должна быть написана разборчиво, без помарок. На обложке необходимо указать фамилию, имя, отчество, фа­культет, курс, номер зачетной книжки. Работа должна содержать список использованной литературы, быть подписана студентом, указана дата выполнения работы.

Пример 1.

На основе данных, приведенных в Приложении и соответствующих варианту 100, требуется:

1. Построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (Х), другой - результативного 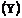. Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.

3. Оценить статистическую значимость параметров регрессии и коэффициента корреляции с уровнем значимости 0,05.

4. Выполнить прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X, составляющим 105% от среднего уровня X. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

Решение:

В качестве признака-фактора в данном случае выберем курсовую цену акций, так как от прибыльности акций зависит величина начисленных дивидендов. Таким образом, результативным будет признак дивиденды, начисленные по результатам деятельности.

Для облегчения расчетов построим расчетную таблицу, которая заполняется по ходу решения задачи. (Таблица 1)

Для наглядности зависимости Yот X представим графически. (Рисунок 2)

Таблица 1 - Расчетная таблица

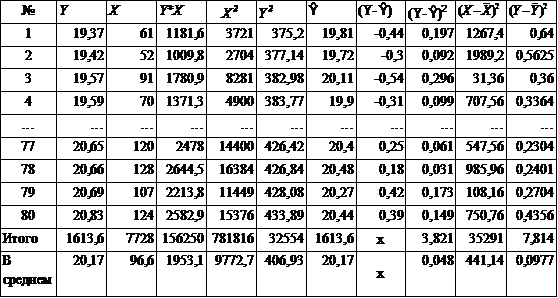
1. Построим уравнение регрессии вида: .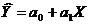

Для этого необходимо определить параметры уравнения 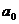и .

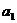Определим ,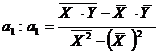

где 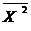- среднее из значений 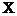, возведенных в квадрат;

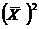- среднее значение 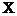в квадрате.

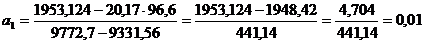
Определим параметр а₀:

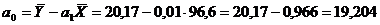
Получим уравнение регрессии следующего вида:

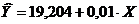
Параметр 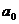показывает, сколько составили бы дивиденды, начисленные по результатам деятельности при отсутствии влияния со стороны курсовой цены акций. На основе параметра 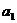можно сделать вывод, что при изменении курсовой цены акций на 1 руб. произойдет изменение дивидендов в ту же сторону на 0,01 млн. руб.

2. Рассчитаем линейный коэффициент парной корреляции и коэффициент детерминации.

Линейный коэффициент парной корреляции определим по формуле:

,

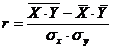Определим 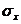и :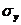

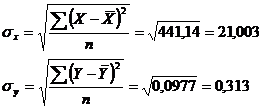
Тогда

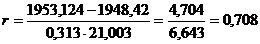
Коэффициент корреляции, равный 0,708, позволяет судить о тесной связи между результативным и факторным признаками .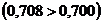

Коэффициент детерминации равен квадрату линейного коэффициента корреляции:

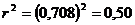
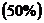
Коэффициент детерминации показывает, что на 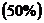вариации начисленных дивидендов зависит от вариации курсовой цены акций, и на 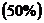- от остальных неучтенных в модели факторов.

3. Оценим значимость параметров уравнения регрессии и линейного коэффициента корреляции по t-критерию Стьюдента. Необходимо сравнить расчетные значения t-критерия для каждого параметра и сравнить его с табличным.

Для расчета фактических значений t-критерия определим :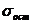

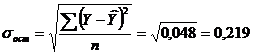
Тогда

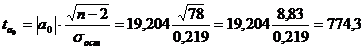
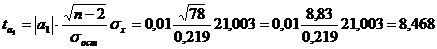
Далее определим 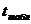_. при уровне значимости 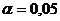и числе степеней свободы равном :

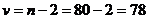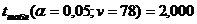
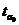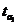Сравним и с 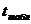: 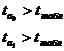, следовательно, оба параметра уравнения регрессии признаются значимыми.

Проверим значимость линейного коэффициента корреляции:

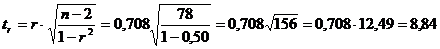
Сравниваем 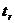с уже известным нам значением 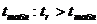, следовательно, линейный коэффициент корреляции существенен.

4. Выполним прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X,составляющим 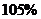от среднего уровня X.

Точечный прогноз рассчитывается по линейному уравнению регрессии:

,

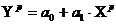В нашем случае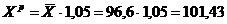

Тогда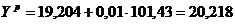

Оценим ошибку прогноза:

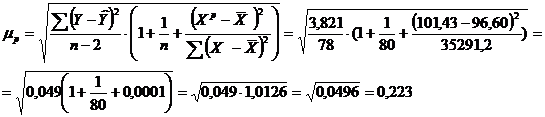
После этого определим интервал, к которому с вероятностью 0,95 принадлежит прогнозное значение признака Y:

,

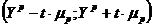где 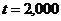– табличное значение t-критерия при 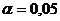и числе степеней свободы

.

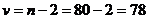В данном случае интервал будет такой:

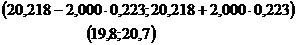
То есть, с вероятностью 0,95 прогнозируемая величина дивидендов при курсовой стоимости акций равной 101,43 руб. будет принадлежать интервалу от 19,8 до 20,7 млн. руб.

Пример 2.

На основе данных, приведенных в Приложении и соответст­вующих варианту 100, требуется:

1. Построить уравнение множественной регрессии. Для этого, ос­тавив признак-результат тем же выбрать несколько признаков-факторов из приложения 1 (границы их наблюдения должны совпадать с границами наблюдения признака-результата, соот­ветствующих Вашему варианту). При выборе факторов нужно руководствоваться как экономическим содержанием, так и формальными подходами (например, матрица парных коэффи­циентов корреляции). Пояснить смысл параметров уравнения.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии (β-коэффициенты).

4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.

6. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

Решение:

По условию задачи, результативный признак должен остаться тот же, значит Y - дивиденды, начисленные по результатам деятельности.В качестве факторных признаков выберем следующие:

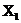– балансовая прибыль;

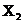- дебиторская задолженность по результатам деятельности.

Определим уравнение регрессии следующего вида:

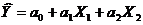
Для определения параметров уравнения связи, а также для дальнейших расчетов построим дополнительную таблицу. (Таблица 2)

Для определения параметров двухфакторного уравнения регрессии необходимо решить систему нормальных уравнений:

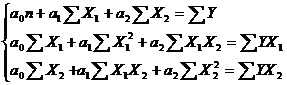
В нашем случае система нормальных уравнений примет вид:

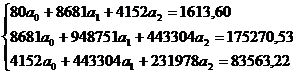
В результате решения данной системы получим следующие коэффициенты регрессии:

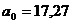
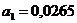
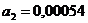
Окончательное уравнение регрессии примет вид:

.

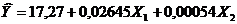При отсутствии влияния со стороны факторных признаков, учтенных в данной модели, значение результативного признака будет составлять 17,2714 млн. руб. При изменении балансовой прибыли на 1 млн. руб. произойдет изменение начисленных дивидендов в ту же сторону на 0,02645 млн. руб., а при изменении дебиторской задолженности на 1 млн. руб. следует ожидать изменения величины начисленных дивидендов на 0,00054 млн. руб.

Определим частные коэффициенты эластичности:

,

.

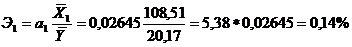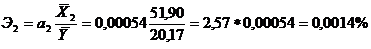Частные коэффициенты эластичности показывают влияние отдельных факторов на результативный показатель. Так, при изменении балансовой прибыли на 1% при неизменности второго фактора произойдет в среднем изменение величины начисленных дивидендов на 0,14%, а при изменении дебиторской задолженности на 1% при фиксированном положении первого фактора произойдет изменение величины начисленных дивидендов в среднем на 0,0014%.

Теперь рассчитаем β-коэффициенты:

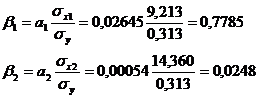
Анализ β-коэффициентов показывает, что на величину начисленных дивидендов из двух исследуемых факторов с учетом уровня их вариации большее влияние оказывает балансовая прибыль .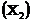

С учетом всех рассчитанных показателей и параметров уравнения регрессии можно сделать вывод о том, что наибольшая связь величины начисленных дивидендов отмечается с размером балансовой прибыли.

Далее, определим парные, частные коэффициенты корреляции и множественный коэффициент корреляции.

I. Парные коэффициенты корреляции: измеряют тесноту связи между двумя из рассматриваемых признаков.

,

,

.

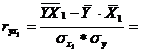
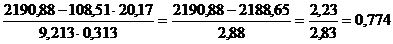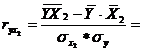
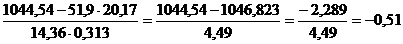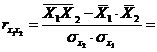
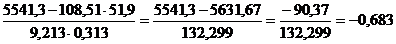Коэффициент корреляции между факторными признаками, равный -0,683, позволяет оставить в модели оба фактора, так как связь между факторами не тесная .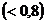

II. Частные коэффициенты корреляции: характеризуют степень влияния одного из факторов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне.

= ,

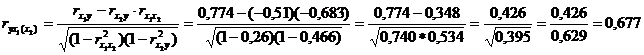
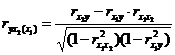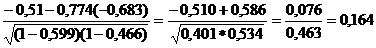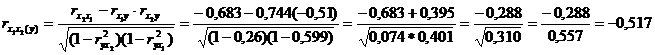
Таблица 2 - Дополнительная таблица

Близкая к тесной прямая связь результативного признака наблюдается с балансовой прибылью (0,677), практически отсутствует связь между начисленными дивидендами и дебиторской задолженностью (0,164).

III. Множественный коэффициент корреляции: показывает тесноту связи между результативным и обоими факторными признаками.

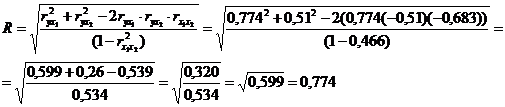
Таким образом, выявлена тесная связь 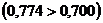между начисленными дивидендами и следующими признаками: балансовая прибыль и дебиторская задолженность.

Множественный коэффициент детерминации определим как квадрат множественного коэффициента корреляции:

.

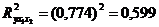На основе коэффициента детерминации делаем вывод, что на 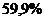вариации величины начисленных дивидендов находится в зависимости от изменения балансовой прибыли и суммы дебиторской задолженности, и на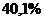 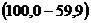– влиянием прочих неучтенных в модели факторов.

На завершительном этапе анализа проверим значимость параметров уравнения регрессии и модели в целом.

Проверим значимость модели в целом с помощью F-статистики Фишера. Для этого определим остаточную дисперсию результативного признака:

,

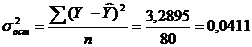Тогда

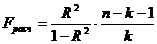= 57,51

,

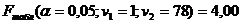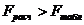, следовательно, модель в целом признается значимой.

Прогнозирование

Для прогнозирования из двух рассмотренных моделей необходимо выбрать ту, у которой ошибка ε наименьшая. Следовательно, при прогнозировании будет использоваться аддитивная модель, так как .

Таким образом, прогнозное значение уровня временного ряда в аддитив­ной модели есть сумма трендовой и сезонной компонент.

Объем товаров, выпущенного фирмой в течение первого по­лугодия ближайшего следующего, т. е. четвертого года, рассчитывается как сумма объемов выпущенных товаров в I и во II кварталах четвертого года, соответственно и . Для определения трендовой компоненты воспользуемся уравнением тренда:

.

Получим:

;

.

Значения сезонной компоненты равны: (I квартал); (II квартал). Таким образом,

;

.

Прогноз объема выпуска товаров фирмой на первое полу­годие 2006 года составит:

усл.ед.

Следует отметить, что для осуществления прогноза по мультипликативной модели, прогнозные значения F определяются как:

.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ЗАДАНИЕ №1 ЛИНЕЙНЫЙ ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

На основе данных, приведенных в таблицах Приложения А и соответст­вующих Вашему варианту, требуется:

1. Построить уравнение линейной парной регрессии одного при­знака от другого. Один из признаков, соответствующих Ваше­му варианту, будет играть роль факторного 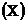, другой - ре­зультативного 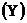. Причинно-следственные связи между при­знаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.

2. Рассчитать линейный коэффициент парной корреляции и ко­эффициент детерминации. Сделать выводы.

3. Оценить статистическую значимость параметров регрессии и коэффициента корреляции с уровнем значимости 0,05.

4. Выполнить прогноз ожидаемого значения признака-результата Y при прогнозном значении признака-фактора X, составляющим 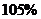от среднего уровня X. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

5. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

6. Самостоятельно дополнительно определить параметры 2 функций, оценить их качество.

ЗАДАНИЕ № 2 МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

На основе данных, приведенных в Приложении А и соответст­вующих Вашему варианту, требуется:

1. Построить уравнение множественной регрессии. Для этого, ос­тавив признак-результат тем же выбрать несколько признаков-факторов из таблицы 1 Приложения А (границы их наблюдения должны совпадать с границами наблюдения признака-результата, соот­ветствующих Вашему варианту). При выборе факторов нужно руководствоваться как экономическим содержанием, так и формальными подходами (например, матрица парных коэффи­циентов корреляции). Пояснить смысл параметров уравнения.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии (β-коэффициенты).

4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать вы­воды.

6. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

ПРИЛОЖЕНИЕ А

Вариант 1				Вариант 2
№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.		№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.
Вариант 3				Вариант 4
№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.		№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.
			20,33					20,46
			20,04					20,07
			19,87					20,23
			20,48					20,26
			20,13					20,28
			20,26					20,52
			19,89					20,28
			19,92					19,97
			19,78					19,97
			20,23					19,57
			20,46					19,94
			20,07					20,29
			20,23					20,83
			20,26					19,59
			20,28					19,76
			20,52					20,19
			20,28					20,66
			19,97					19,95
			19,97					20,61
			19,57					20,03
			19,94					19,78
			20,29					20,22
			20,83					19,78
			19,59					20,09
			19,76					20,13
Вариант 5				Вариант 6
№ наб-люде-ния	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.		№ наб-люде-ния	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.
А					А
		20,33					20,46
		20,04					20,07
		19,87					20,23
		20,48					20,26
		20,13					20,28
		20,26					20,52
		19,89					20,28
		19,92					19,97
		19,78					19,97
		20,23					19,57
		20,46					19,94
		20,07					20,29
		20,23					20,83
		20,26					19,59
		20,28					19,76
		20,52					20,19
		20,28					20,66
		19,97					19,95
		19,97					20,61
		19,57					20,03
		19,94					19,78
		20,29					20,22
		20,83					19,78
		19,59					20,09
		19,76					20,13
Вариант 7				Вариант 8
№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.		№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.
							19,97
							19,97
							19,57
							19,94
							20,29
							20,83
							19,59
							19,76
							20,19
							20,66
							19,95
							20,61
							20,03
							19,78
							20,22
							19,78
							20,09
							20,13
							20,56
							20,51
							19,71
							20,1
							20,32
							20,37
							20,03

ЗАДАНИЕ №3 ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ

Задание:
1. Построить автокорреляционную функцию данного временного ряда и коррелограмму.
2. Сделать выводы относительно структуры временного ряда.
3. Построить аддитивную и мультипликативную модели временного ряда.
4. Оценить качество моделей и выбрать лучшую.
5. Выполнить прогноз по лучшей модели на 2015 год
представив его в расчетной форме и графически.

Вариант 1								Вариант 2
Динамика выручки торгового предприятия, млн.руб.				Динамика выручки торгового предприятия, млн.руб.
год	квартал	У, млн. руб.						год	квартал	У, млн. руб.
		26,4								126,4
		21,3								121,3
		18,3								118,3
		21,5								121,5
		38,5								138,5
		34,2								134,2
		27,4								127,4
		32,5								132,5
		49,5								149,5
		48,1								148,1
		32,1								132,1
		45,8								145,8
		56,4								156,4
		50,3								150,3
		38,2								138,2
		51,3								151,3
		69,3								169,3
		60,8								160,8
		55,1								155,1
		69,7								169,7
		85,4								185,4
		75,1								175,1
		62,3								162,3
		57,3								157,3
											<