Основы теории Марковских процессов

Тольятти, 2011

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное

учреждение среднего профессионального образования

Тольяттинский политехнический колледж

(ФГОУ СПО ТПК)

УТВЕРЖДАЮ

Методист УПО №4

_____________ Л.Г. Светличная

___.___.20___

ЗАДАНИЕ

на курсовое проектирование по дисциплине

«Математические методы»

Студенту специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем»____________________________________________________

группы В-31__________________________________________________________________

Фамилия, имя, отчество__Гаспарян Армен Арамович________________________________

Тема проекта __Марковские случайные процессы___________________________________

_____________________________________________________________________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Начало проектирования _12.01.11_______Окончание проектирования__21.06.11____________

Руководитель курсового проекта _Кондурар М. В., Кондурар Н. Н.________________ ___

Задание получил__________________/_Гаспарян А. А._______________________________

Календарный план работы над проектом

Наименование этапов работы	Сроки выполнения этапов	Степень готовности к полному объему, %	Время выполнения
Постановка задачи. Написание плана.
Написание теоретической части курсового проекта.
Написание практической части
Написание введения, заключения. Анализ полученных результатов.
Представление работы руководителю.
Защита курсового проекта.

Дата выдачи задания_12.01.11____________________________________________________

Руководитель курсового проектирования__________________________________________

Задание принял к исполнению___________________________________________________

Содержание

Введение 3

1 Основы теории Марковских процессов............................................................... 5

1.1...... Основные понятия........................................................................................... 5

1.2...... Уравнения Колмогорова................................................................................. 7

1.3...... Марковский процесс с дискретным временем ............................................ 7

1.4 Марковские случайные процессы................................................................. 9

2 Расчет предметных вероятностей ...................................................................... 11

2.1...... Задача 1 .......................................................................................................... 11

2.2 Задача 2 .......................................................................................................... 14

2.3 Задача 3 .......................................................................................................... 18

Заключение............................................................................................................................ 22

Список используемых источников..................................................................................... 23

Введение

Теория марковских случайных процессов – обширный раздел теории вероятности с широким спектром приложений (физические явления типа диффузии или перемешивания шихта во время плавки в доменной печи, процессы образования очередей).

Основные понятия теории Марковских цепей ввел А.А. Марков в 1907г. С тех пор эту теорию развивали многие ведущие математики. В последнее время обнаружилась важная роль цепей Маркова в биологических и социологических науках. Показано, что для решения всех типов задач достаточно рассмотреть только два типа Марковских цепей. Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, особое внимание Марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений. Практическое применение теории Марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров. Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания. В теории систем массового обслуживания (в дальнейшем просто -CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Цели данного курсового проекта:

1.Изучить тему «Марковские случайные процессы»

2.Проанализировать литературу по вышеуказанной теме.

3.Подобрать, обобщать материал по теме «Марковские случайные процессы»

4.Выполнить практическую часть курсового проекта в виде решения трех задач с использованием метода Гаусса и программных средств MS Excel 2010 и Mathcad 2000.

Основы теории Марковских процессов

Основные понятия

Марковские случайные процессы многие изменяющиеся во времени сложные системы целесообразно рассматривать как случайные процессы, ход которых зависят от ряда случайных факторов, сопровождающих это развитие.

Для того чтобы вычислить числовые параметры, характеризующие такие системы, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы.

Пусть имеется некоторая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, производственный процесс, вычислительная машина, информационная сеть и т. д.). Если состояние системы S меняется во времени случайным, заранее непредсказуемым образом, говорят, что в системе протекает случайный процесс.

Конкретное протекание каждого из таких процессов зависит от ряда случайных, заранее непредсказуемых факторов.

Для математического описания многих случайных процессов может быть применен аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов. Случайный процесс, протекающий в системе S, называется марковским (или «процессом без последействия»), если он обладает следующим свойством: для каждого момента времени вероятность любого состояния системы в будущем (при t > ) зависит только от ее состояния в настоящем (при t= ) и не зависит от того, когда и каким образом система пришла в это состояние (т. е. как развивался процесс в прошлом) .

Другими словами, в марковском случайном процессе будущее развитие зависит только от его настоящего состояния и не зависит от «предыстории» процесса.

На практике часто встречаются случайные процессы, которые с той или другой степенью приближения можно считать марковскими. Теория марковских случайных процессов является обширным разделом теории вероятностей с широким спектром различных приложений — от описания физических явлений типа диффузии или перемешивания шихты во время плавки в доменной печи до процессов образования очередей или распространения мутаций в биологической популяции.

Марковские случайные процессы делятся на классы по некоторым признакам, в зависимости от того, как и в какие моменты времени система может менять свои состояния.

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы, можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое.

Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями.

При анализе случайных процессов с дискретными состояниями удобно пользоваться так называемым графом состояний и переходов (ГСП) (Рисунок1). ГСП графически изображает возможные состояния системы и ее возможные переходы из состояния в состояние.

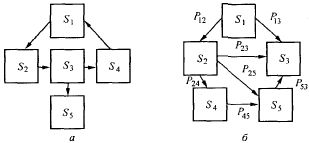
Рисунок1. Граф состояний и переходов: а — обычный; б — размеченный

Пусть имеется система S с n дискретными состояниями:

Каждое состояние изображается прямоугольником, а возможные переходы («перескоки») из состояния в состояние — стрелками, соединяющими эти прямоугольники.

Заметим, что стрелками отмечаются только непосредственные переходы из состояния в состояние; если система может перейти из состояния в только через то стрелками отмечаются только переходы и но не

Пусть система S — прибор, который может находиться в одном из пяти возможных состояний: — исправен, работает; — неисправен, ожидает осмотра; — осматривается; — ремонтируется; — списан.

Уравнения Колмогорова

При t стремящимся к бесконечности вероятность будет стремиться, каким то приделам если эти приделы существуют, то они называются финальными вероятностями и находятся по следующим правилам: слева в уравнениях стоит предельная вероятность данного состояния, умноженная на суммарную интенсивность всех потоков, идущих из данного состояния. А справа сумма произведений интенсивностей всех потоков, входящих в данное состояние на вероятности тех состояний, из которых исходит поток.

Задача 1

1

3 2 1 4

Рисунок 7

Решение:

3p1=3p2+3p3;

4p2=p1+4p4;

5p3+2p1+4p4;

8p4=2p3+p2;

P1+p2+p3+p4=1;

Решаем систему уравнений методами Гаусса

1 -4 0 4 0

2 0 -5 4 0

0 1 2 -8 0

1 1 1 1 1

Занулили 1-ый стролбец

1 -4 0 4 0

0 8 -5 -4 0

0 1 2 -8 0

0 5 1 -3 1

Нашли единицу в 2-ом столбце и поменяли местами 3-ю и 2-ую строки

1 -4 0 4 0

0 1 2 -8 0

0 8 -5 -4 0

0 5 1 -3 1

Занулили 2-ой стролбец

1 0 8 -28 0

0 1 2 -8 0

0 0 -21 60 0

0 0 -9 37 1

Получили единицу в 3-ем столбце раделив 3-ю строку на -21

1 0 8 -28 0

0 1 2 -8 0

0 0 1 -20/7 0

0 0 -9 37 1

Занулили 3-ий стролбец

1 0 0 -36/7 0

0 1 0 -16/7 0

0 0 1 -20/7 0

0 0 0 79/7 1

Ответ:

p1 = 0,4556 p2 = 0,2025 p3 = 0,2531 p4 = 0,0886

Рисунок 8- Решение задачи 1, с помощью метода Гаусса

Решение задачи с помощью электронной таблицы Excel представлены на рисунке 9. Формулы для решения задачи представлены на рисунке 10. Решение задачи с помощью программы Mathcad Professional представлены на рисунке11.

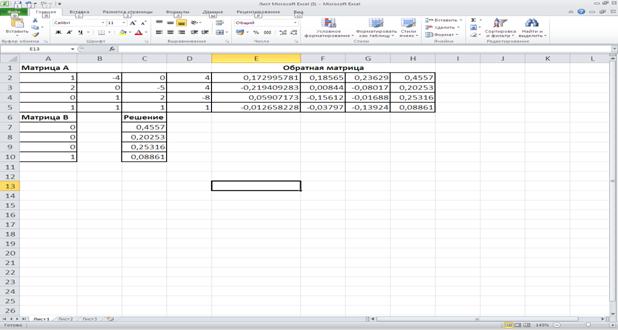
Рисунок 9-Решение задачи с помощью электронной таблицы Excel

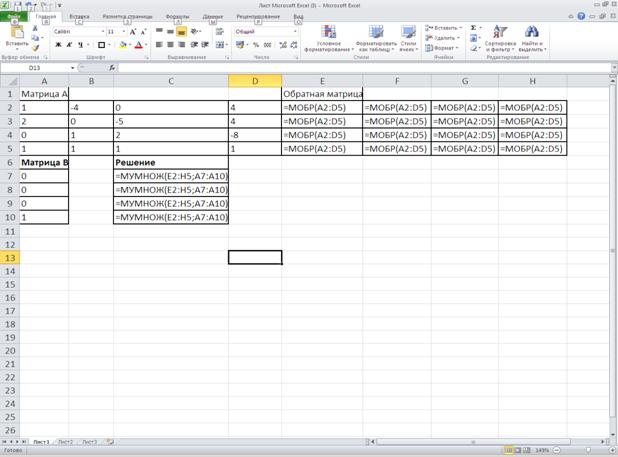
Рисунок 10-Формулы для решения задачи

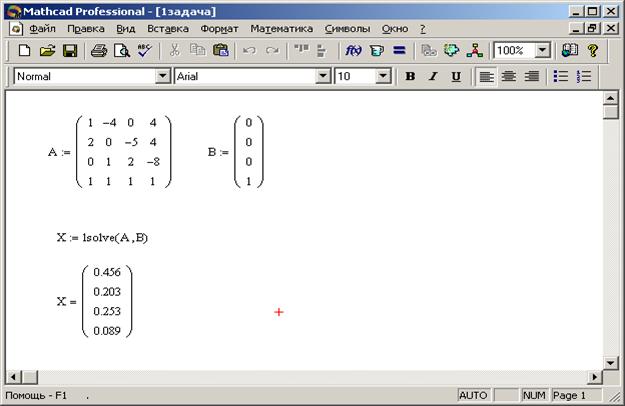
Решение задачи с помощью программы Mathcad Professional представлены на рисунке11

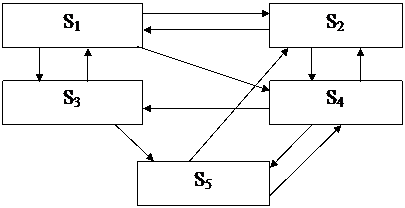
Задача 2

4

2 3 5 1

1 3

Рисунок 12

Решение:

6p1=3p2+3p3;

8p2=4p1+p4+2p5;

4p3+2p1+4p4;

8p4=2p1+5p2+4p5;

6p5=p3+p4;

p1+p2+p3+p4+p5=1;

Решаем систему уравнений методами Гаусса

6 -3 -3 0 0 0

-4 8 0 -1 -2 0

-2 0 4 -4 0 0

-2 -5 0 8 -4 0

1 1 1 1 1 1

Нашли единицу в 1-ом столбце и поменяли местами 5-ую и 1-ую строки

1 1 1 1 1 1

-4 8 0 -1 -2 0

-2 0 4 -4 0 0

-2 -5 0 8 -4 0

6 -3 -3 0 0 0

Занулили 1-ый стролбец

1 1 1 1 1 1

0 12 4 3 2 4

0 2 6 -2 2 2

0 -3 2 10 -2 2

0 -9 -9 -6 -6 -6

Получили единицу в 2-ом столбце раделив 2-ую строку на 12

1 1 1 1 1 1

0 1 1/3 1/4 1/6 1/3

0 2 6 -2 2 2

0 -3 2 10 -2 2

0 -9 -9 -6 -6 -6

Занулили 2-ой стролбец

1 0 2/3 3/4 5/6 2/3

0 1 1/3 1/4 1/6 1/3

0 0 16/3 -5/2 5/3 4/3

0 0 3 43/4 -3/2 3

0 0 -6 -15/4 -9/2 -3

Получили единицу в 3-ем столбце раделив 3-ю строку на 16/3

1 0 2/3 3/4 5/6 2/3

0 1 1/3 1/4 1/6 1/3

0 0 1 -15/32 5/16 1/4

0 0 3 43/4 -3/2 3

0 0 -6 -15/4 -9/2 -3

Занулили 3-ий стролбец

1 0 0 17/16 5/8 1/2

0 1 0 13/32 1/16 1/4

0 0 1 -15/32 5/16 1/4

0 0 0 389/32 -39/16 9/4

0 0 0 -105/16 -21/8 -3/2

Ответ:

p1 = 0,2426 p2 = 0,1643 p3 = 0,3209 p4 = 0,1996 p5 = 0,0724

Рисунок 13- Решение задачи 2 с помощью метода Гаусса

Решение задачи с помощью электронной таблицы Excel представлены на рисунке 14. Формулы для решения задачи представлены на рисунке 15. Решение задачи с помощью программы Mathcad Professional представлены на рисунке16.

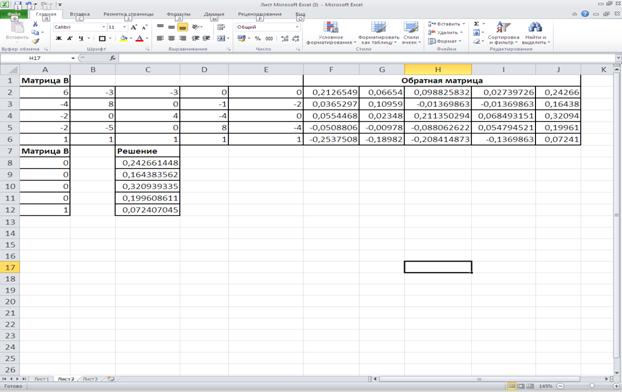
Рисунок 14-Решение задачи с помощью электронной таблицы Excel

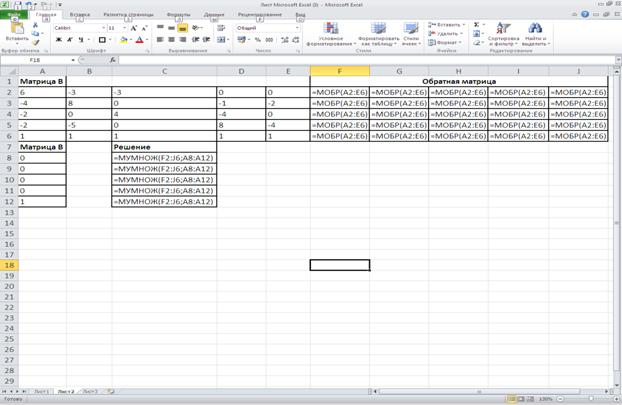
Рисунок 15-Формулы для решения задачи

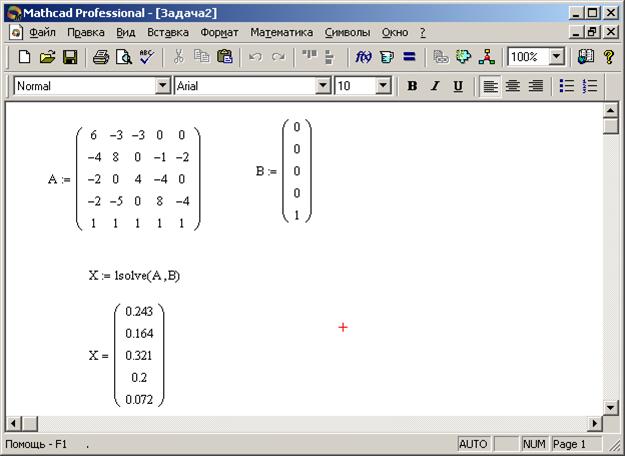
Решение задачи с помощью программы Mathcad Professional представлены на рисунке16

Задача 3

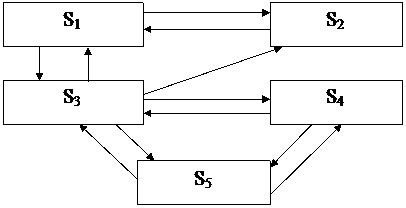4

2 3

4 3

2 1

Рисунок 17

Решение:

6p1=3p2+3p3;

3p2=4p1+2p3;

11p3+3p1+4p4+2p5;

7p4=5p3+4p5;

6p5=p3+3p4;

p1+p2+p3+p4+p5=1;

Решаем систему уравнений методами Гаусса

0 -3 -3 6 0 0

-4 3 -2 0 0 0

-3 0 11 -4 -2 0

0 0 -5 7 -4 0

1 1 1 1 1 1

Нашли единицу в 1-ом столбце и поменяли местами 5-ую и 1-ую строки

1 1 1 1 1 1

-4 3 -2 0 0 0

-3 0 11 -4 -2 0

0 0 -5 7 -4 0

0 -3 -3 6 0 0

Занулили 1-ый стролбец

1 1 1 1 1 1

0 7 2 4 4 4

0 3 14 -1 1 3

0 0 -5 7 -4 0

0 -3 -3 6 0 0

Получили единицу в 2-ом столбце раделив 2-ую строку на 7

1 1 1 1 1 1

0 1 2/7 4/7 4/7 4/7

0 3 14 -1 1 3

0 0 -5 7 -4 0

0 -3 -3 6 0 0

Занулили 2-ой стролбец

1 0 5/7 3/7 3/7 3/7

0 1 2/7 4/7 4/7 4/7

0 0 92/7 -19/7 -5/7 9/7

0 0 -5 7 -4 0

0 0 -15/7 54/7 12/7 12/7

Получили единицу в 3-ем столбце раделив 3-ю строку на 92/7

1 0 5/7 3/7 3/7 3/7

0 1 2/7 4/7 4/7 4/7

0 0 1 -19/92 -5/92 9/92

0 0 -5 7 -4 0

0 0 -15/7 54/7 12/7 12/7

Занулили 3-ий стролбец

1 0 0 53/92 43/92 33/92

0 1 0 29/46 27/46 25/46

0 0 1 -19/92 -5/92 9/92

0 0 0 549/92 -393/92 45/92

0 0 0 669/92 147/92 177/92

Ответ:

p1 = 0,1397 p2 = 0,2891 px3 = 0,1542 p4 = 0,2216 p5 = 0,1951

Рисунок 18- Решение задачи 3 с помощью метода Гаусса

Решение задачи с помощью электронной таблицы Excel представлены на рисунке 19. Формулы для решения задачи представлены на рисунке 20. Решение задачи с помощью программы Mathcad Professional представлены на рисунке 21.

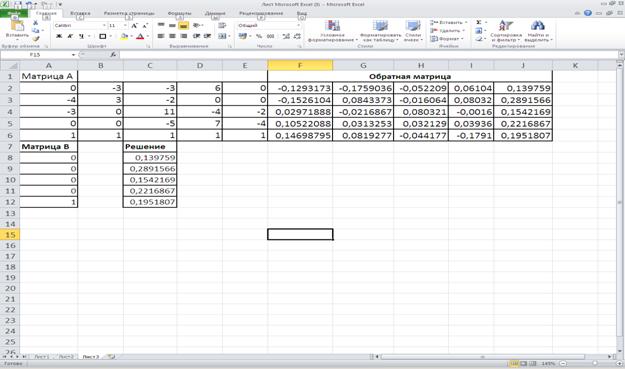
Рисунок 19-Решение задачи с помощью электронной таблицы Excel

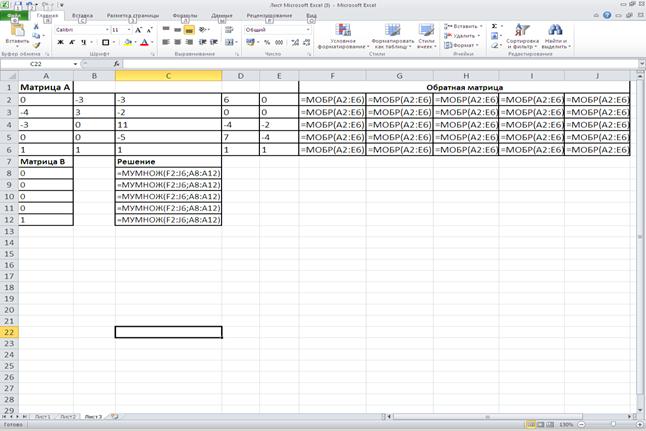
Рисунок 20-Формулы для решения задачи

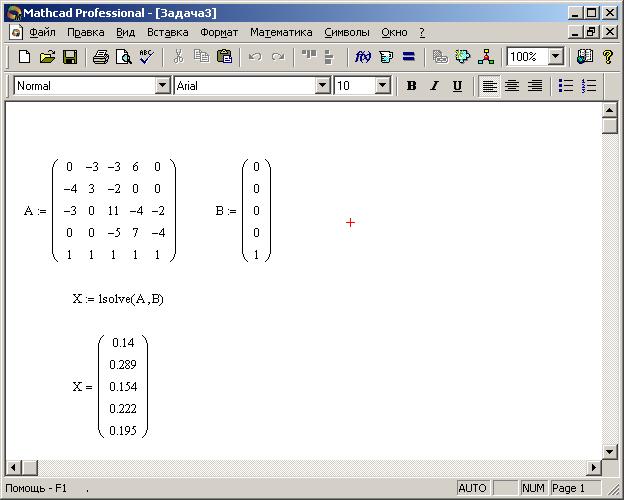
Решение задачи с помощью программы Mathcad Professional представлены на рисунке21

Заключение

В данном курсовом проекте рассмотрена теория Марковских случайных процессов.

Мы проводили практическое исследование, с помощью таких программных средств, как MS Excel 2010 и Mathcad 2000.

При написании данного курсового проекта были проанализированы работы: Хэмди А. Таха Введение в исследование операций-М: Издательский дом ”Вильямс”, 2001, Н.Ш. Кремер Исследование операций в экономике-М: Издательское объединение “ЮНИТИ”, 1997, Г.П. Фомин Математические методы и модели в коммерческой деятельности М:”Финансы и статистика”,2005. Наиболее полезной оказалось книга Хэмди А. Таха Введение в исследование операций-М: Издательский дом ”Вильямс”, 2001, потому что эта книга отличается простотой и доступностью изложенной в ней информации.

На основе решённых задач можно дать следующие рекомендации: при решении задач более легким, наглядным и удобным является метод Гаусса.

На основе данных примеров мы можем рассчитать почти любую экономическую задачу.

Программное средство Mathcad 2000 удобно для подобных задач. Отличается удобным решением и простотой обращения.

Тольятти, 2011

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное

учреждение среднего профессионального образования

Тольяттинский политехнический колледж

(ФГОУ СПО ТПК)

УТВЕРЖДАЮ

Методист УПО №4

_____________ Л.Г. Светличная

___.___.20___

ЗАДАНИЕ

на курсовое проектирование по дисциплине

«Математические методы»

Студенту специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем»____________________________________________________

группы В-31__________________________________________________________________

Фамилия, имя, отчество__Гаспарян Армен Арамович________________________________

Тема проекта __Марковские случайные процессы___________________________________

_____________________________________________________________________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Начало проектирования _12.01.11_______Окончание проектирования__21.06.11____________

Руководитель курсового проекта _Кондурар М. В., Кондурар Н. Н.________________ ___

Задание получил__________________/_Гаспарян А. А._______________________________

Календарный план работы над проектом

Наименование этапов работы	Сроки выполнения этапов	Степень готовности к полному объему, %	Время выполнения
Постановка задачи. Написание плана.
Написание теоретической части курсового проекта.
Написание практической части
Написание введения, заключения. Анализ полученных результатов.
Представление работы руководителю.
Защита курсового проекта.

Дата выдачи задания_12.01.11____________________________________________________

Руководитель курсового проектирования__________________________________________

Задание принял к исполнению___________________________________________________

Содержание

Введение 3

1 Основы теории Марковских процессов............................................................... 5

1.1...... Основные понятия........................................................................................... 5

1.2...... Уравнения Колмогорова................................................................................. 7

1.3...... Марковский процесс с дискретным временем ............................................ 7

1.4 Марковские случайные процессы................................................................. 9

2 Расчет предметных вероятностей ...................................................................... 11

2.1...... Задача 1 .......................................................................................................... 11

2.2 Задача 2 .......................................................................................................... 14

2.3 Задача 3 .......................................................................................................... 18

Заключение............................................................................................................................ 22

Список используемых источников..................................................................................... 23

Введение

Теория марковских случайных процессов – обширный раздел теории вероятности с широким спектром приложений (физические явления типа диффузии или перемешивания шихта во время плавки в доменной печи, процессы образования очередей).

Основные понятия теории Марковских цепей ввел А.А. Марков в 1907г. С тех пор эту теорию развивали многие ведущие математики. В последнее время обнаружилась важная роль цепей Маркова в биологических и социологических науках. Показано, что для решения всех типов задач достаточно рассмотреть только два типа Марковских цепей. Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, особое внимание Марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений. Практическое применение теории Марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров. Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания. В теории систем массового обслуживания (в дальнейшем просто -CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Цели данного курсового проекта:

1.Изучить тему «Марковские случайные процессы»

2.Проанализировать литературу по вышеуказанной теме.

3.Подобрать, обобщать материал по теме «Марковские случайные процессы»

4.Выполнить практическую часть курсового проекта в виде решения трех задач с использованием метода Гаусса и программных средств MS Excel 2010 и Mathcad 2000.

Основы теории Марковских процессов

Основные понятия

Марковские случайные процессы многие изменяющиеся во времени сложные системы целесообразно рассматривать как случайные процессы, ход которых зависят от ряда случайных факторов, сопровождающих это развитие.

Для того чтобы вычислить числовые параметры, характеризующие такие системы, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы.

Пусть имеется некоторая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, производственный процесс, вычислительная машина, информационная сеть и т. д.). Если состояние системы S меняется во времени случайным, заранее непредсказуемым образом, говорят, что в системе протекает случайный процесс.

Конкретное протекание каждого из таких процессов зависит от ряда случайных, заранее непредсказуемых факторов.

Для математического описания многих случайных процессов может быть применен аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов. Случайный процесс, протекающий в системе S, называется марковским (или «процессом без последействия»), если он обладает следующим свойством: для каждого момента времени вероятность любого состояния системы в будущем (при t > ) зависит только от ее состояния в настоящем (при t= ) и не зависит от того, когда и каким образом система пришла в это состояние (т. е. как развивался процесс в прошлом) .

Другими словами, в марковском случайном процессе будущее развитие зависит только от его настоящего состояния и не зависит от «предыстории» процесса.

На практике часто встречаются случайные процессы, которые с той или другой степенью приближения можно считать марковскими. Теория марковских случайных процессов является обширным разделом теории вероятностей с широким спектром различных приложений — от описания физических явлений типа диффузии или перемешивания шихты во время плавки в доменной печи до процессов образования очередей или распространения мутаций в биологической популяции.

Марковские случайные процессы делятся на классы по некоторым признакам, в зависимости от того, как и в какие моменты времени система может менять свои состояния.

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы, можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое.

Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями.

При анализе случайных процессов с дискретными состояниями удобно пользоваться так называемым графом состояний и переходов (ГСП) (Рисунок1). ГСП графически изображает возможные состояния системы и ее возможные переходы из состояния в состояние.

Рисунок1. Граф состояний и переходов: а — обычный; б — размеченный

Пусть имеется система S с n дискретными состояниями:

Каждое состояние изображается прямоугольником, а возможные переходы («перескоки») из состояния в состояние — стрелками, соединяющими эти прямоугольники.

Заметим, что стрелками отмечаются только непосредственные переходы из состояния в состояние; если система может перейти из состояния в только через то стрелками отмечаются только переходы и но не

Пусть система S — прибор, который может находиться в одном из пяти возможных состояний: — исправен, работает; — неисправен, ожидает осмотра; — осматривается; — ремонтируется; — списан.

Уравнения Колмогорова

При t стремящимся к бесконечности вероятность будет стремиться, каким то приделам если эти приделы существуют, то они называются финальными вероятностями и находятся по следующим правилам: слева в уравнениях стоит предельная вероятность данного состояния, умноженная на суммарную интенсивность всех потоков, идущих из данного состояния. А справа сумма произведений интенсивностей всех потоков, входящих в данное состояние на вероятности тех состояний, из которых исходит поток.