Построение вероятностной бумаги закона нормального распределения

При построении вероятностной бумаги закона нормального распределения по оси абсцисс откладывают значения показателя надежности Т_др в произвольном масштабе, а по оси ординат – значение накопленной опытной вероятности åР_i. За начальную точку отсчета по оси абсцисс принимают значение показателя надежности, близкое к началу зоны рассеивания, а если нет смещения t_см – его нулевое значение.

За начальную точку отсчета по оси ординат принимают значения F₀=0,01. Квантиль Н_к интегральной функции этого значения равен Н_к(0,01)=Н_к(0,99)=2,326 (см. таблицу Б7 приложения Б).

Расстояние Y_i в мм произвольной отметки F_i или åР_i от начальной точки оси ординат пропорционально разности квантилей этих точек, умноженной на масштабный коэффициент М:

М[Н_к(0,01)-Н_к(F_i)]. (1.32)

Приняв М=50 и приравняв F_i= 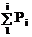для отметок F_i или 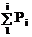получаем:

Y_i(мм)=50[2,326- Н_к(F_i)].

Так, например, отметка на оси ординат (F_i)=0,05(по таблице Б7 приложения Б квантиль Н_к(0,05) или, что одно и тоже, Н_к(0,95) равен 1,645), будет находиться от начальной точки оси на расстоянии:

Y_i(F_i=0,05)=50[2,326- 1,645]=34,0 мм

Для упрощения расчетов при построении функциональной сетки ЗНР в таблице Б9 приложения Б приведены расстояния отметок на оси ординат в миллиметрах в интервале F_i=åР_i=0,02-0,98 через 0,01.

Пользуясь данными таблицы Б9 приложения Б и задавшись масштабом оси абсцисс (в 1мм 40 мото.ч.), определяют координаты в миллиметрах выбранных точек информации.

Координаты точек по оси абсцисс определяют следующим образом:

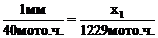, следовательно Х₁=30,7 мм;

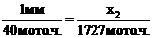, следовательно Х₂=43,2 мм;

и т.д.

Таблица 6 – Координаты опытных точек ЗНР

№i	Tдрi		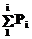X, мм	Y, мм
2,5 40,5 58,5 63,5 65,5 68,5		0,04 0,15 0,37 0,57 0,70 0,82 0,89 0,92 0,96	30,7 43,2 55,6 68,1 80,5 93,0 105,4 117,9 130,3	28,8 64,5 99,7 125,1 142,5 162,1 177,6 186,6 203,8

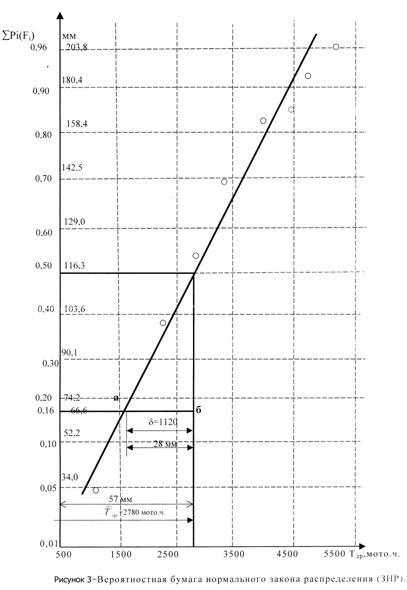
Далее опытные точки наносят на функциональную сетку вероятностной бумаги ЗНР и проводят между ними интегральную прямую так, чтобы количество точек с обеих сторон прямой было бы примерно одинаково, а их отклонения от прямой минимальны (рисунок 3).

При ЗНР среднее значение показателя надежности 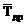соответствует накопленной вероятности åР_i=0,5. Поэтому абсцисса точки пересечения горизонтали åР_i=0,5, проведенной на расстоянии 116,3 мм от начала координат, с интегральной прямой соответствует в заданном масштабе среднему значению показателя надежности .

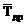В нашем случае (см. рисунок 3):

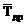=57×40+500=2780 мото.ч.

Среднее квадратическое отклонение s (второй параметр ЗНР) определяют графическим методом на основе уравнения:

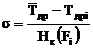, (1.33)

где Н_к(F_i) – квантиль интегральной функции.

Из этого уравнения видно, что в случае Н_к(F_i)=1,0, s= .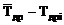

Определено, что Н_к(F_i)=1,0 при F_i=0,16. Следовательно, величина s равна длине отрезка аб (разность абсциссы 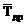и абсциссы точки пересечения горизонтали åР_i=0,16, проведенная на расстоянии 66,6 мм от начала координат, см. таблицу Б9 приложения Б).

Для нашего примера:

s=28×40=1120 мото.ч.