Частные случаи нормального закона распределения. 1 страница
Стандартное нормальное распределение
Определение 17.1. Стандартное нормальное (или нормированное) распределение с параметрами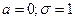 
имеет плотность распределения или дифференциальную функцию распределения случайной величины 
(рис. 17.1)
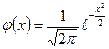
и функцию вероятностей или интегральную функцию распределения (рис. 17.2)
.
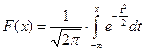Графики этих функций имеют вид, где для наглядности изображения используются различные масштабные единицы измерения по осям координат.
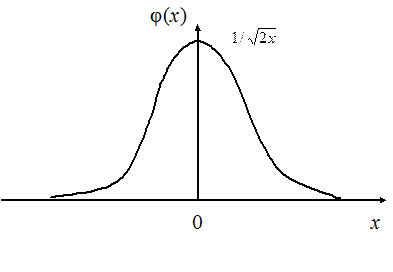
Рис. 17.1
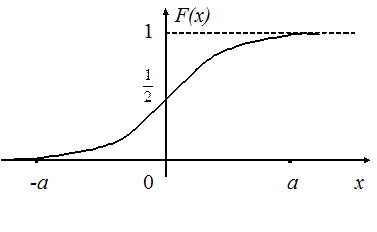
Рис. 17.2
Распределение Пирсона
Определение 17.2. Распределением Пирсона или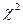 
(хи-квадрат) – распределением с k степенями свободы называют суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону, т.е.
,
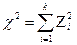где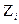 
имеет нормальное распределение пр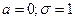и и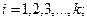 
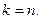
Плотность вероятности или дифференциальная функция распределения 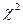имеет вид:
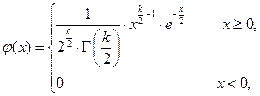
где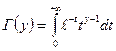 
– гамма-функция Эйлера, которая для целых положительных значений 
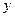равна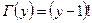 
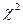! -распределение случайной величины асимметрично и облает положительной, т.е. правосторонней асимметрией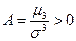 
. График 
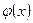при различных значениях 
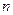имеет вид (рис. 17.3).
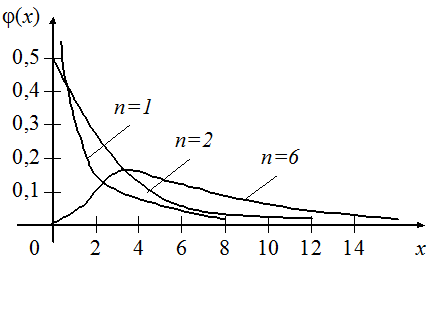
Рис. 17.3
При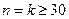 
распределение случайной величины 
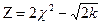близко к нормальному закону. Распределение 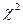определяется одним параметром – числом степеней свободы 
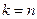. С увеличением числа степеней свободы 
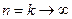распределение медленно приближается к нормальному.
Распределение Стьюдента.
Определение 3.Распределением Стьюдента или t- распределением с k степенями свободы называется распределение случайной величины t, равной отношению нормированной нормальной случайной величины Z к корню квадратному из независимой случайной величины от Z, распределенной по закону 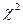с k степенями свободы, деленной на k, т.е.
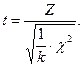
С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному, уже при к>30. Плотность вероятности распределения Стьюдента имеет вид:
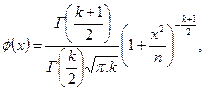
где 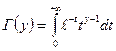– гамма-функция Эйлера. График функции 
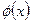более пологий по сравнению с нормальной кривой (рис. 17.4).
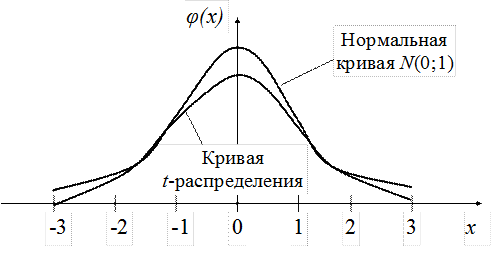
Рис. 17.4
Значит,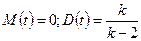 
.
Вопросы для самопроверки
1. Какие события называются случайными? Элементарными? Достоверными? Невозможными? Приведите примеры случайных событий.
2. Какие события называются совместными? Несовместными? Противоположными? Приведите примеры.
3. Какие события образуют полную группу несовместных событий?
4. Приведите примеры полных групп событий.
5. Какое событие называется суммой или объединением нескольких событий?
6. Что называется относительной частотой случайного события? Что называется статистической вероятностью события и каковы ее свойства?
7. Сформулируйте классическое определение вероятности события. Перечислите ее свойства. В каких пределах изменяется вероятность случайного события?
8. Какое событие называется произведением или пересечением нескольких событий?
9. Сформулируйте теорему сложения вероятностей для несовместных событий.
10. Чему равна сумма вероятностей несовместных событий, образующих полную группу?
11. Какая вероятность называется условной вероятностью?
12. Какие события называются независимыми? Зависимыми?
13. Сформулируйте теоремы умножения вероятностей зависимых и независимых событий.
14. Как следует вычислять вероятность появления хотя бы одного из нескольких совместных событий (теорема сложения вероятностей совместных событий)?
15. Сформулируйте формулу полной вероятности.
16. Сформулируйте формулу вероятности гипотез, т.е. формулу Байеса.
17. При решении каких задач применяется формула полной вероятности и формула Байеса?
18. Сформулируйте схему Бернулли или схему повторных испытаний.
19. Сформулируйте формулу Бернулли. При решении каких задач применяется эта формула?
20. Сформулируйте общие правила комбинаторики: правило суммы и правило произведения.
21. Сформулируйте определения генеральной и выборочной совокупностей.
22. Какие выборки называются размещениями, перестановками и сочетаниями? По каким формулам вычисляют их число?
23. Дайте определение наивероятнейшего числа при повторных испытаниях и приведите правило его вычисления.
24. Сформулируйте локальную теорему Лапласа. Перечислите свойства локальной функции Лапласа и изобразите ее график. При решении каких задач применяется локальная формула Лапласа?
25. Сформулируйте интегральную теорему Лапласа. Перечислите свойства интегральной функции Лапласа и изобразите ее график. При решении каких задач применяется интегральная формула Лапласа?
26. Сформулируйте и запишите формулы Пуассона. При решении каких задач применяются формулы Пуассона?
27.Какая величина называется случайной величиной?
28.Дайте определение дискретной и непрерывной случайных величин. Приведите примеры дискретных и непрерывных случайных величин.
29.Что называется законом распределения случайной величины?
30.Что называется рядом распределения дискретной случайной величины?
31.Дайте определение функции распределения вероятности (интегральной функции распределения). Перечислите свойства функции распределения.
32.Как, зная функцию распределения, найти вероятность попадания случайной величины в заданный интервал?
33.В чем состоит различие графиков функций распределения дискретной и непрерывной случайных величин?
34.Дайте определение плотности распределения вероятностей (дифференциальной функции распределения). Перечислите свойства плотности распределения. Пригодно ли понятие плотности распределения вероятностей для дискретной случайной величины?
35.Как, зная плотность распределения, найти вероятность попадания случайной величины в заданный интервал?
36.Что называется математическим ожиданием дискретной случайной величины? Запишите формулу его вычисления.
37.Что называется математическим ожиданием непрерывной случайной величины? Запишите формулу его вычисления.
38.Как можно истолковать математическое ожидание случайной величины?
39.Что называется модой и медианой случайной величины?
40.Перечислите свойства математического ожидания случайной величины?
41.Дайте определение дисперсии дискретной случайной величины; непрерывной случайной величины. Запишите формулы их вычисления. Перечислите свойства дисперсии случайной величины.
42.Что называется средним квадратическим отклонением случайной величины?
43.Что характеризуют дисперсия и среднее квадратическое отклонение случайной величины?
44.Что называется начальным моментом k-го порядка случайной величины? Что представляет собой начальный момент первого порядка?
45.Что называется центральным моментом k-го порядка? Чему равен центральный момент первого порядка? Что представляет собой центральный момент второго порядка?
46.Что характеризует центральный момент третьего порядка? Что называется коэффициентом асимметрии (скошенности)? Что можно сказать о кривой распределения в зависимости от знака коэффициента асимметрии?
47.Что характеризует центральный момент четвертого порядка? Что называется эксцессом случайной величины? Что можно сказать о кривой распределения в зависимости от знака эксцесса случайной величины?
48.Что называется линейным абсолютным отклонением и для характеристики чего оно применяется?
49.Какой распределение вероятностей называется биномиальным? Чему равны математическое ожидание и дисперсия случайной величины, имеющей биномиальное распределение?
50.Какое распределение называется распределением Пуассона? Чему равны математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона?
51.Какое распределение случайной величины называется равномерным распределением?
52.Какое распределение случайной величины называется показательным распределением?
53.Какое распределение случайной величины называется нормальным распределением? Какими параметрами определяется дифференциальный закон нормального распределения?
54.Как называется график плотности вероятности нормального распределения и каковы его свойства? Чему равна площадь под нормальной кривой? Как влияют параметры плотности вероятности на форму нормальной кривой?
55.Как можно вычислить вероятность попадания случайной величины в заданный интервал? В интервал симметричный относительно математического ожидания, распределенной по нормальному закону?
56.Что называется функцией Лапласа и каковы ее свойства?
57.Сформулируйте правило трех сигм.
Индивидуальные задания по теме «Случайные события»
ЗАДАЧА 1 (№ 1–10)
В ящике лежит n картофелин четырех сортов: «Синеглазка», «Белорусская ранняя», «Колпашенская», «Адретта», причем «Синеглазки» – n1 штук, «Белорусской ранней» – n2 штук, «Колпашенской» – n3 штук, «Адретты» – n4 штук и n1+n2+n3 +n4 =n.
Для опыта берутся наудачу m картофелин. Определить вероятность того, что среди взятых m картофелин будет m1 штук сорта «Синеглазка», m2 штук сорта «Белорусская ранняя», m3 штук сорта «Колпашенская», m4 штук сорта «Адретта» и m1+m2+m3+m4= m.
(№ 11–20)
На четырех станках изготовлено «n» деталей, причем на первом станке n1 деталей, на втором станке n2 деталей, на третьем станке n3 деталей, на четвертом станке n4 деталей и n1+n2+n3 +n4 =n.
Для контроля качества случайным образом берутся m деталей. Определить вероятность того, что среди взятых m деталей будет m1 деталей с первого станка, m2 деталей со второго станка, m3 деталей с третьего станка, m4 деталей с четвертого станка и m1+m2+m3+m4= m.
(№ 21–40)
В магазин поступили телевизоры с четырех заводов и их число составляет «n» штук, причем с первого завода поступило n1 штук, со второго завода поступило n2 штук, с третьего завода поступило n3 штук, с четвертого завода поступило n4 штук и n1+n2+n3 +n4 =n.
Для контроля качества случайным образом берутся m телевизоров. Определить вероятность того, что среди взятых «m» телевизоров будет m1 штук с первого завода, m2 штук со второго завода, m3 штук с третьего завода и m4 штук с четвертого завода и m1+m2+m3+m4= m.
| № | n1 | n2 | n3 | n4 | m1 | m2 | m3 | m4 | № | n1 | n2 | n3 | n4 | m1 | m2 | m3 | m4 | |
ЗАДАЧА 2 (№ 1–10)
На полке лежат n учебников, из них к учебников по математике. Студент берет наудачу m учебников. Какова вероятность того, что среди взятых m учебников будет s учебников по математике.
(№ 11–20)
В бассейне содержится n рыб, из которых к карпов, остальные лещи. Наудачу выловили m рыб. Определить вероятность того, что среди выловленных m рыб попадутся s карпов.
(№ 21–40)
В корзине находится штук n штук яиц, среди которых к штук качественные. Наудачу отобрали m яиц. Определить вероятность того, что среди отобранных m яиц будет s яиц качественных.
| № | n | к | m | s | № | n | к | m | s | |
ЗАДАЧА 3 (№ 1–10)
В корзине m лежат фруктов, из них n яблок, остальные груши. Из корзины наудачу берут два фрукта. Какое из событий более вероятно:
Событие А – оба фрукта одинаковые.
Событие В – Одно яблоко и одна груша?
(№ 11–20)
В ящике лежат «m» электрических лампочек, из них «n» лампочек качественных. Из ящика наугад берут две лампочки. Какое из двух событий окажется более вероятным:
Событие А – обе лампочки качественные или обе некачественные.
Событие В – одна качественная и одна некачественная?
(№ 21–40)
На клумбе растет «m» цветков лилий, из них «n» цветков белой лилии, остальные желтые лилии. Наудачу срывают две лилии. Какое из двух событий более вероятно:
Событие А – сорваны лилии одного цвета.
Событие В – сорваны лилии разного цвета?
| № | m | n | № | m | n | № | m | n | № | m | n | |||
ЗАДАЧА 4 (№ 1–10)
В мастерской работают два мотора независимо друг от друга. Известно, что в течение часа первый мотор не потребует внимания мастера составляет К1%, а второй мотор в течение часа не потребует внимания мастера составляет К2%. Найдите вероятность того, что:
1. Оба мотора в течение часа потребуют внимания мастера.
2. Оба мотора в течение часа не потребуют внимания мастера.
3. Потребует внимания только один мотор.
4. Потребует внимания хотя бы один мотор?
(№ 11–20)
Два стрелка стреляют в цель независимо друг от друга. Вероятность попадания в цель первого стрелка равна К1%, а второго стрелка – К2%. Найдите вероятность того, что:
1. Оба стрелка не поразят цель.
2. Оба стрелка поразят цель.
3. Один стрелок поразит цель, а второй нет.
4. Хотя бы один стрелок поразит цель?
(№ 21–40)
Исследователь разыскивает нужные ему сведения в двух справочниках. Вероятность того, что эти сведения находятся в первом справочнике равна К1%, а находятся во втором справочнике – К2%. Найдите вероятность того, что требуемые сведения:
1. Не содержатся ни в одном справочнике.
2. Содержатся в обоих справочниках.
3. Содержатся только в одном справочнике.
4. Хотя бы в одном справочнике содержатся нужные сведения?
| № | К1 | К2 | № | К1 | К2 | № | К1 | К2 | № | К1 | К2 | |||