Оцените тесноту связи с помощью показателей корреляции и детерминации.

Лабораторная работа №1.

«Корреляционный и регрессионный анализ- Математический метод оценки взаимосвязей экономических явлений»

Выполнила:Насруллаева З.Ш.

Проверила:Шахбанова З.И

Махачкала 2015

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными y и x, т.е. модель вида

y = f(x),

где у – зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная, (признак – фактор).

Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор.

Различают линейные и нелинейные регрессии.

Линейная регрессия: y=a+b×x+ε.

Нелинейные регрессии делятся на два класса: регрессии, нели­нейные относительно включенных в анализ объясняющих перемен­ных, но линейные по оцениваемым параметрам, и регрессии, нели­нейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

· полиномы разных степеней y=a+b₁×x+b₂×x²+b₃× x³+ε

· равносторонняя гипербола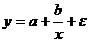

Регрессии, нелинейные по оцениваемым параметрам:

· степенная y=a× x^b×ε

· показательная y=a× b^x×ε

· экспоненциальная y=e^a+b×x×ε

Перед нами поставлены ряд задач:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи

2. Рассчитайте параметры уравнений линейной регрессии.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации

4. "Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05.

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Задача 4.

Имеются данные районов за ноябрь 1997 года по территориям Волго-Вятского, Центрально-Черноземного и Поволжского в таблице 1.4.

Район	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального харак­тера, тыс. руб., х
Волго-Вятский
Респ. Марий Эл
Респ. Мордовия
Чувашская Респ.
Кировская обл.
Нижегородская обл. -
Центрально-Черноземный
Белгородская обл.
Воронежская обл.
Курская обл.
Липецкая обл.
Тамбовская обл.
Поволжский
Респ. Калмыкия
Респ. Татарстан
Астраханская обл.
Волгоградская обл.
Пензенская обл.
Саратовская обл.
Ульяновская обл.

Решение.

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи

В парной регрессии выбор математической формы зависимости между у и х может быть осуществлен следующими методами: графическим, аналитическим, экспериментальным.

Наиболее наглядным методом является - графический. Он основан на поле корреляции.

На основе регрессионных данных у и х строим корреляционное поле:

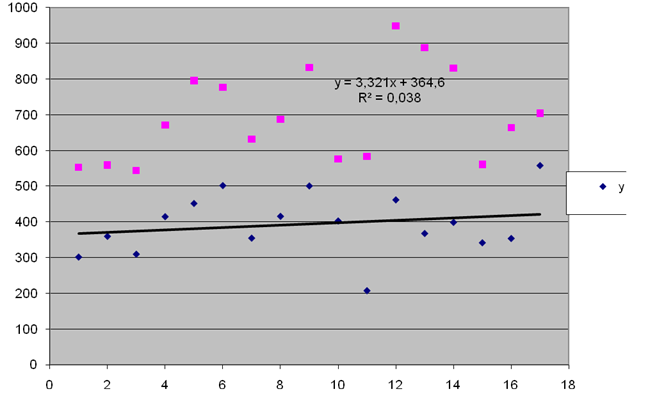
2. Рассчитайте параметры уравнений линейной регрессии.

Линейная регрессия сводится к построению уравнения вида y=a+b×x

Построение уравнения регрессии сводится в первую очередь к расчету его параметров - а и b. Они могут быть определены разными методами. Наиболее распространенным методом, является метод наименьших квадратов (МНК).

Следует отметить, что рассчитываются не истинные значения a и b, а только оценки, которые могут быть хорошими или плохими.

Система нормальных уравнений при оценке параметров имеет вид:

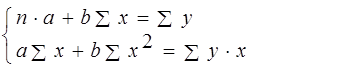
Решая систему получим

, ,

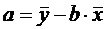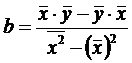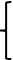
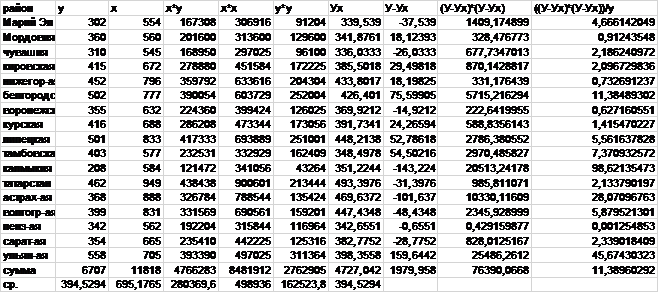В нашем случае система нормальных уравнений имеет вид:

17a+11818b=6707

11818a+8481912b=4766283

Решив ее получим: a=123,7474; b=0,389516

Параметр b называется выборочным коэффициентом регрессии. Его величина показывает, насколько единиц изменится результат с изменением фактора на 1 единицу.

Параметр а не имеет экономической интерпретации. Например, если а < 0, то попытка его экономической интерпретации приводит абсурду.

В нашем случае параметр b показывает, что изменение фактора на 1 единицу приведет к увеличению результата на 0,389516. А параметр а не имеет экономического смысла, но т.к. а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Запишем уравнение регрессии: у=123,7474+0,389516x

При вычислении на ЭВМ получим следующие данные:

Значение коэффициента B=0,39 Значение коэффициента, а=123,75

Среднеквадратичное отклонение= 0,14 Среднеквадратичное отклонение, а=0,27

Коэффициент детерминации=0,35 Среднеквадратичное отклонение, y=0,196

F-статистика=7,93 Число степеней свободы=15

Регрессионная сумма квадратов=40406,17 Остаточная сумма квадратов=0,58

Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

F-критерий Фишераиспользуется для оценки значимости уравнения регрессии. Для этого выполняется сравнение фактического F_факг и критического (табличного) F_табл зна­чений F-критерия Фишера. F_факт определяется из соотношения зна­чений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

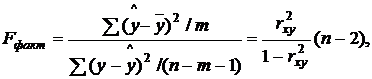
где п — число единиц совокупности;

m - число параметров при переменных x..

F_табл - это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна. Обычно а принимает­ся равной 0,05 или 0,01.

Если F_табл < F_факг, то H_о - гипотеза о случайной природе оцени­ваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл > F_факг, то гипотеза H_о не от­клоняется и признается статистическая не значимость, ненадежность y уравнения регрессии.

Получим: F_{факт =} 0,345954/(1-0,345954)*15=7,9

Можно сделать вывод, что нулевая гипотеза неверна, уравнение считается значимым.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05.

Прогнозное значение y_p определяется путем подстановки в урав­нение регрессии 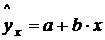соответствующего (прогнозного) зна­чения Х_р. Вычисляется средняя стандартная ошибка прогноза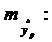

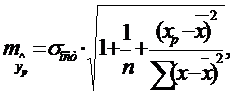
где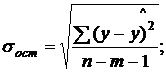

и строится доверительный интервал прогноза:

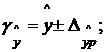
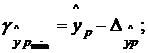
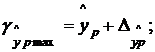
где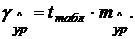

Вычислим прогнозное значение Упр, при условии что Хпр увеличится на 10%.

Xp=695,17*1.1=764,69

Yp=123,74+0.389*764.69=421,6

Лабораторная работа №1.

«Корреляционный и регрессионный анализ- Математический метод оценки взаимосвязей экономических явлений»

Выполнила:Насруллаева З.Ш.

Проверила:Шахбанова З.И

Махачкала 2015

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными y и x, т.е. модель вида

y = f(x),

где у – зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная, (признак – фактор).

Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор.

Различают линейные и нелинейные регрессии.

Линейная регрессия: y=a+b×x+ε.

Нелинейные регрессии делятся на два класса: регрессии, нели­нейные относительно включенных в анализ объясняющих перемен­ных, но линейные по оцениваемым параметрам, и регрессии, нели­нейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

· полиномы разных степеней y=a+b₁×x+b₂×x²+b₃× x³+ε

· равносторонняя гипербола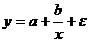

Регрессии, нелинейные по оцениваемым параметрам:

· степенная y=a× x^b×ε

· показательная y=a× b^x×ε

· экспоненциальная y=e^a+b×x×ε

Перед нами поставлены ряд задач:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи

2. Рассчитайте параметры уравнений линейной регрессии.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации

4. "Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05.

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Задача 4.

Имеются данные районов за ноябрь 1997 года по территориям Волго-Вятского, Центрально-Черноземного и Поволжского в таблице 1.4.

Район	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального харак­тера, тыс. руб., х
Волго-Вятский
Респ. Марий Эл
Респ. Мордовия
Чувашская Респ.
Кировская обл.
Нижегородская обл. -
Центрально-Черноземный
Белгородская обл.
Воронежская обл.
Курская обл.
Липецкая обл.
Тамбовская обл.
Поволжский
Респ. Калмыкия
Респ. Татарстан
Астраханская обл.
Волгоградская обл.
Пензенская обл.
Саратовская обл.
Ульяновская обл.

Решение.

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи

В парной регрессии выбор математической формы зависимости между у и х может быть осуществлен следующими методами: графическим, аналитическим, экспериментальным.

Наиболее наглядным методом является - графический. Он основан на поле корреляции.

На основе регрессионных данных у и х строим корреляционное поле:

2. Рассчитайте параметры уравнений линейной регрессии.

Линейная регрессия сводится к построению уравнения вида y=a+b×x

Построение уравнения регрессии сводится в первую очередь к расчету его параметров - а и b. Они могут быть определены разными методами. Наиболее распространенным методом, является метод наименьших квадратов (МНК).

Следует отметить, что рассчитываются не истинные значения a и b, а только оценки, которые могут быть хорошими или плохими.

Система нормальных уравнений при оценке параметров имеет вид:

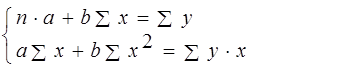
Решая систему получим

, ,

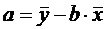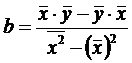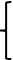
В нашем случае система нормальных уравнений имеет вид:

17a+11818b=6707

11818a+8481912b=4766283

Решив ее получим: a=123,7474; b=0,389516

Параметр b называется выборочным коэффициентом регрессии. Его величина показывает, насколько единиц изменится результат с изменением фактора на 1 единицу.

Параметр а не имеет экономической интерпретации. Например, если а < 0, то попытка его экономической интерпретации приводит абсурду.

В нашем случае параметр b показывает, что изменение фактора на 1 единицу приведет к увеличению результата на 0,389516. А параметр а не имеет экономического смысла, но т.к. а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Запишем уравнение регрессии: у=123,7474+0,389516x

При вычислении на ЭВМ получим следующие данные:

Значение коэффициента B=0,39 Значение коэффициента, а=123,75

Среднеквадратичное отклонение= 0,14 Среднеквадратичное отклонение, а=0,27

Коэффициент детерминации=0,35 Среднеквадратичное отклонение, y=0,196

F-статистика=7,93 Число степеней свободы=15

Регрессионная сумма квадратов=40406,17 Остаточная сумма квадратов=0,58

Оцените тесноту связи с помощью показателей корреляции и детерминации.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такового показателя выступает линейный коэффициент корреляции r. Формула линейного коэффициента корреляции имеет вид:

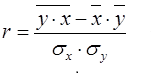
Где сигма x и сигма y определяются по следующим формулам:

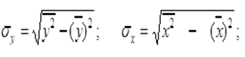
Коэффициент корреляции должен находится в пределах: -1<r <1.

В нашем примере при вычислении на ЭВМ коэффициент корреляции равен 0,59

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

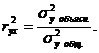
Соответственно величина 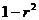характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

В нашем случае коэффициент детерминации= 0,345. Таким образом, уравнением регрессии объясняется 34,5% дисперсии результативного признака, а на долю прочих факторов приходится лишь 65,5% ее дисперсии (т.е. остаточная дисперсия).