Для равновесия произвольной системы сил необходимо и достаточно, чтобы три суммы проекций всех сил на оси координат и три суммы моментов всех сил относительно осей координат равнялись нулю.
Если условия равновесия (3) содержат известные и неизвестные силы конкретной задачи, то их называют уравнениями равновесия.
Следует отметить, что при составлении уравнений равновесия за центр приведения может быть выбрана любая другая точка, так как при выборе нового центра приведения O1 получим, что MO1 = mO1(R) + MO. И если для центра O выполняются условия (2), то для любого другого центра приведения, например O1, будет R = 0 и MO1 = 0.
Условия равновесия для частных случаев произвольной системы 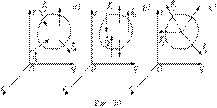 сил в аналитической форме.
сил в аналитической форме.
Рассмотрим условия равновесия систем сил приложенных к твердому телу не произвольно, а с ограничениями. Эти условия получим из выражений (3) для произвольной системы сил (рис. 30, a), которая является общим случаем.
Система параллельных сил. В этой системе все силы параллельны какой либо прямой. Пусть, например, все силы параллельны оси OZ (рис.30, b). Тогда вырождаются в тождества (0 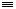 0) первое, второе и шестое из выражений (3), а остаются третье, четвертое и пятое из них, потому что силы системы на оси OX и OYне проектируются, а момента относительно оси OZ силы не создают, так как они ей параллельны. Следовательно, возможны только три условия или три уравнения равновесия для системы параллельных сил:
0) первое, второе и шестое из выражений (3), а остаются третье, четвертое и пятое из них, потому что силы системы на оси OX и OYне проектируются, а момента относительно оси OZ силы не создают, так как они ей параллельны. Следовательно, возможны только три условия или три уравнения равновесия для системы параллельных сил:
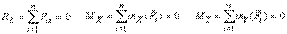 | (4) |
Система сходящихся сил. Линии действия всех сил этой системы пересекаются в одной точке. В п. Система пар сил. мы на основании только аксиом статики доказали, что система сходящихся сил приводится к одной силе и сформулировали для нее условия равновесия. Получим эти условия равновесия иначе. Так как к паре сил эта система приведена быть не может, то MO = 0, и четвертое, пятое и шестое из выражений (3) вырождаются в тождества. Следовательно, возможны только три условия или три уравнения равновесия для системы сходящихся сил:
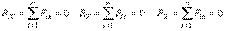 | (5) |
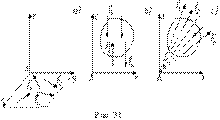
Плоская система сил. Все силы этой системы лежат в одной плоскости. Пусть, например, это будет плоскость XAY, где A произвольный центр приведения (рис.31, a). Силы этой системы на ось AZ не проектируются и моментов относительно осей AX иAY не создают, так как лежат в плоскости XAY (п. 13). Поэтому третье, четвертое и пятое из выражений (3) вырождаются в тождества и остаются три выражения. Причем в шестом выражении (3) по пятому свойству момента силы относительно оси (п. 13) выполняется равенство
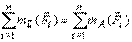
Учитывая это, получим условия равновесия для плоской системы сил:
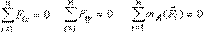 | (6) |
Таким образом, для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы проекций сил на оси координат и сумма алгебраических моментов всех сил относительно любой точки плоскости.
Выражения (6) являются основной формой условия равновесия для плоской системы сил. Существуют еще две дополнительные формы условий, которые мы сформулируем без доказательства.
I-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю три суммы моментов сил системы относительно трех точек плоскости, не лежащих на одной прямой:
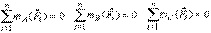 | (7) |
II-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы моментов сил системы относительно двух точек плоскости и сумма проекций сил системы на ось, не перпендикулярную прямой, соединяющей эти точки:
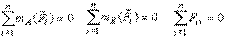 | (8) |
Последние две формы условий равновесия чаще всего используются для расчета ферм методом сечений (методом Риттера).
Плоская система параллельных сил. Силы этой системы лежат в одной плоскости и параллельны друг другу. Пусть, например, они параллельны оси OY (рис.31, b). Тогда первое из выражений (6) вырождается в тождество, и остаются два условия или уравнения равновесия для плоской системы параллельных сил:
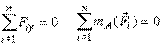 | (9) |
Плоская система сходящихся сил. Силы этой системы лежат в одной плоскости и линии их действия пересекаются в одной точке. С этой точкой совместим начало координат (рис. 31, c). Тогда третье из выражений (6) вырождается в тождество (силы системы не создают моментов относительно точки A , так как они проходят через эту точку) и остаются два условия или уравнения равновесия для плоской системы сходящихся сил:
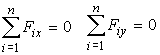 | (10) |
Итак, для каждой конкретной системы сил, приложенной к твердому телу, мы можем записать (в той или иной форме) определенное число уравнений равновесия. Равновесие плоской системы сходящихся сил определяется двумя уравнениями, а для определения равновесия твердого тела под действием произвольной системы сил можно составить систему из шести уравнений. В системе уравнений число неизвестных не должно превышать числа уравнений, иначе система не имеет однозначного решения.
Поэтому статически определенными являются задачи, в которых число неизвестных не превышает числа уравнений равновесия. Иначе задачи не могут быть решены методами статики и являются статически неопределенными.
Статически неопределенные задачи могут быть решены методами сопротивления материалов и теории упругости, в которых учитывается связь между силой и деформациями тела (закон Гука).
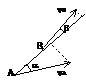
36)Плоское движение твердого тела.
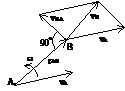 Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят. Скорости точек тела при плоском движении:
Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят. Скорости точек тела при плоском движении: 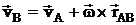 ;
; 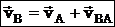 , vBA= w×BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А. Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcosa = vBcosb.
, vBA= w×BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А. Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcosa = vBcosb.
37) 37.Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
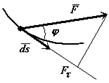 Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
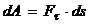 .
. 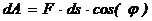 ,
,
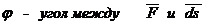
Единицей измерения работы в СИ является – 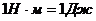
При  при
при 
Частные случаи: 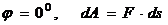
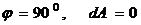
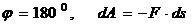
Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы.
Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.
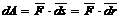
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.
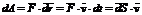
Если сила 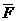 задана своими проекциями (
задана своими проекциями ( 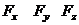 ) на оси координат и элементарное перемещение задано своими проекциями (
) на оси координат и элементарное перемещение задано своими проекциями ( 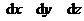 ) на оси координат, то элементарная работа силы равна:
) на оси координат, то элементарная работа силы равна:
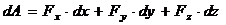 (аналитическое выражение элементарной работы).
(аналитическое выражение элементарной работы).
Работа силы на любом конечном перемещении 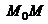 равна взятому вдоль этого перемещения интегралу от элементарной работы.
равна взятому вдоль этого перемещения интегралу от элементарной работы.
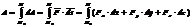
38) Теорема об изменения кинетического момента системы.Формулировка теоремы: производная по времени от кинетического момента системы относительно неподвижной оси 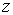 равна сумме моментов всех внешних сил относительно этой оси, т. е.
равна сумме моментов всех внешних сил относительно этой оси, т. е.
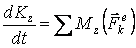 . (2.4)
. (2.4)
Рассмотрим методику решения задач с помощью этой теоремы:
– изображаем систему в произвольный момент времени, показывая все внешние силы, действующие на систему;
– находим сумму моментов внешних сил относительно оси;
– находим кинетический момент системы относительно оси;
– находим производную по времени от кинетического момента системы;
– составляем уравнение (2.4);
– решаем это уравнение, находим искомые величины.
Закон сохранения кинетических моментов. Формулировка закона: если при движении системы сумма моментов внешних сил относительно неподвижной оси 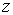 равна нулю, то кинетический момент системы относительно этой оси есть величина постоянная, т. е. если
равна нулю, то кинетический момент системы относительно этой оси есть величина постоянная, т. е. если
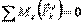 , то
, то 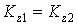 , (2.5)
, (2.5)
где 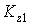 и
и 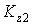 – кинетические моменты в 1-м и 2-м положениях системы.
– кинетические моменты в 1-м и 2-м положениях системы.
Используя условие (2.5), можно решать задачи по определению начальных или конечных скоростей тел системы, определять законы изменения этих скоростей.
Рассмотрим методику решения подобных задач:
– изображаем систему в произвольный момент времени, показывая все внешние силы; убеждаемся, что сумма моментов внешних сил относительно неподвижной оси 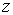 равна нулю, т. е. таким образом:
равна нулю, т. е. таким образом:
– изображаем систему в первом положении и находим 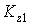 ;
;
– изображаем систему во втором положении и находим 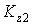 ;
;
| – используем равенство (2.5), составляем уравнение, из которого находим искомую величину. |
