Разложение плоского движения твердого тела на поступательное и вращательное движение. Угловая скорость и угловое ускорение тела при плоском движении

Плоским движением твердого тела называется такое его движение, при котором каждая его точка все время движется в одной и той же плоскости

Теорема. Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое — относительное.

В частности, движение плоской фигуры в ее плоскости относительно системы , расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат , начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат вращением вокруг подвижной оси, перпендикулярной плоской фигуре и проходящей через выбранный полюс.

Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое можно перевести двумя перемещениями — поступательнымперемещением в плоскости фигуры вместе с каким —либо полюсом и поворотом в той же плоскости вокруг этого полюса.

Скорость любой точки тела в плоском движении равна векторной или геометрической сумме скорости полюса в поступательном движении тела совместно с полюсом и скорости вращения точки вокруг полюса во вращательном движении тела вокруг полюса:

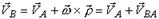
где VB - скорость точки, VA - скорость полюса, VBA - скорость вращения точки вокруг полюса. Причем: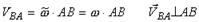

где ,ω - модуль угловой скорости и величина вектора угловой скорости; AB - расстояние между точкой и полюсом, равное радиусу вращения точки вокруг полюса.

Отметим, что угловая скорость не зависит от выбора полюса, и поэтому при использовании теоремы для решения задач за полюс может быть выбрана любая точка тела, скорость которой известна в неподвижной системе координат.

Ускорение любой точки тела в плоском движении равно геометрической сумме ускорения точки тела в поступательном движении совместно с полюсом и ускорения вращения точки вокруг полюса во вращательном движении тела вокруг полюса.

Дифференцируя по времени выражение (2), получаем:

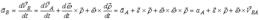
В последнем выражении вектор углового ускорения тела ε направлен по оси вращения тела, совпадающей с осями Az* и Az1 , так как при плоском движении вектор ω не изменяет своего направления в пространстве, двигаясь параллельно самому себе. То есть распределение ускорений в базовой системе координат такое же, как и при вращении тела вокруг неподвижной оси.

Очевидно, что aA является ускорением полюса или ускорением поступательного движения базовой системы координат и тела совместно с полюсом. Согласно векторным формулам для ускорений точек тела при вращательномдвижениию вектор касательного ускорение вращения вокруг полюса равен: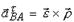

Отметим, что теорема о сложении ускорений точек тела в плоском движении часто используется для решения задач. Ускорения могут быть найдены в двух основных случаях, когда: 1) расстояние от полюса до мгновенного центра скоростей в процессе движения остается постоянной величиной; 2) ускорение одной точки тела (полюса) и траектория второй точки тела известны.