Элементарный и полный импульс силы.

Действие силы 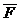на материальную точку в течении времени 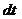можно охарактеризовать элементарным импульсом силы .

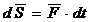Полный импульс силы 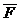за время 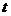, или импульс силы 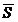, определяется по формуле 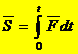. (Полный интеграл за время 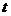от элементарного импульса).

В частном случае, если сила 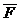постоянна и по величине , и по направлению ( ), .

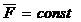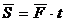Проекции импульса силы на прямоугольные декартовы оси координат равны:

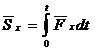
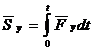
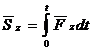
Единицей измерения импульса в СИ является –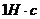

17.Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором какие либо две точки тела будут оставаться неподвижными. Прямая, проведенная через эти точки называется осью вращения твердого тела.

Вращательное движение твердого тела определено, если задан как функция времени угол, измеряемый в радианах:

φ =φ(t), где φ(t) – непрерывная дважды дифференцируемая функция времени.

Алгебраическая угловая скорость вращения тела φ =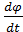

Единица измерения в СИ – рад/с

Изменение угловой скорости тела во времени характеризуется угловым ускорением. Алгебраическое значение углового ускорения тела определяется как первая производная от алгебраического значения угловой скорости или вторая производная по времени от угла поворота тела вокруг неподвижной оси:

φ =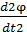

Вращательное движение называется ускоренным, если 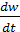>0 и замедленным, если 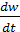<0, при ε(t)=0 тело вращается равномерно, в этом случае ω=const.

Скорость точки тела, совершающего вращательное движение вокруг неподвижной оси, определяется векторной формулой Эйлера

υ=ω*r

Модуль скорости определяется как:

υ=|ω*r|= ω*r*sin (ω^r)= ω*h

Скорости точек при вращении вокруг неподвижной оси направлены по касательной к окружности радиусом h в соответствии с направлением угловой скорости тела

Ускорение точки тела a= ε*r + ω* υ

Слагаемые в правой части представляют собой касательную a_r= ε*r и нормальную a_n= ω* υ= ω *(ω*r) составляющие ускорения точки

Модуль касательного ускорения равен:

|a_r|=|ε*r|=ε*r*sin(ε^r)=ε*h

Вектор a_n всегда направлен по нормали к траектории точки в сторону ее вогнутости (к оси вращения тела).Модуль нормального ускорения равен:

|a_n|=|ω*υ|= ω*υ*sin(π/2)=ω²*h

Полное ускорение точки тела, вращающегося вокруг неподвижной оси, равно:

a= a_r+ a_n

Его численное значение (модуль) определяется по формуле:

a=√ a_r²₊ a_n²=√(εh)²+(ω²h)²=h√ε²+ ω⁴

Таким образом, модули скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси, прямо пропорциональны кратчайшему расстоянию от них до оси вращения, причем, чем дальше находится точка от оси вращения, тем больше ее скорость и ускорение

18. Формула кинетического момента вращающегося твёрдого тела относительно оси его вращения. Теорема об изменении кинетического момента и следствие из неё.

v_i=wh_i L_iz=I_z*w, где Iz – момент инерции относительно оси вращения.

I_z=∑Δm_ih² L_z=∑Δm_iv_ih_i

Теорема об изменении кинетического момента:

Производная от кинетического момента по времени равна сумме моментов внешних сил. P_i^e-внешние силы

dL_o/dt=∑m_o(P_i^e)

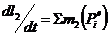-в проекции на ось координат

Следствие1: основное уравнение вращательного движения d(I_zw)/dt=∑m_z(P_i^e)

В частном случае когда вращается твёрдого тела относительно неподвижной оси, тогда момент инерции не меняется.

I_z*dw/dt=∑m_z(P_i^e) осн. ур-ніе I_zε=∑m_z*(P_i^e) динамики вращ. движ.

Следствие2: закон сохранения кинетического момента.

Если сумма моментов внешних сил относительного какого-нибудь центра или оси =0, то соответствующий кинетический момент есть величина постоянная.

∑m_z*(P_i^e)=0, L_z-const.