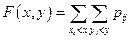Непрерывные случайные величины. Функция распределения непрерывной случайной величины.

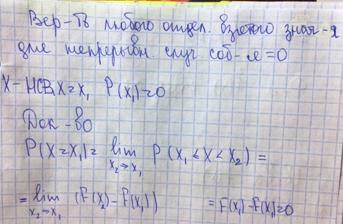
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x:
F(X) = P(X<x)
Функция распределения обладает следующими свойствами:
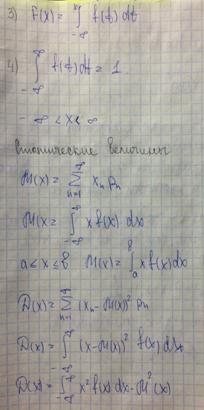
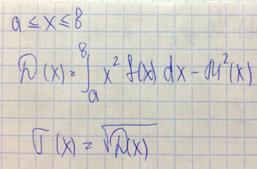
МодойM0(X) случайной величины X называется ее наиболее вероятное значение (для которого вероятность Pi или плотность вероятности φ(x) достигает максимума).
МедианойMe(X) непрерывной случайной величины X называется такое ее значение, для которого
P(X < Me(X)) = P(X > Me(X)) = 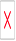 .
.
Начальным моментом порядка случайной величины X называется математическое ожидание k-ой степени этой величины:
 .
.
Если X – дискретная случайная величина, то 

Если X – непрерывная случайная величина, то

Центральным моментом k-ого порядка случайной величины X называется величина
 и
и
Для дискретной величины

Для непрерывной величины

Напомним, что для обозначения математического ожидания используется буква “a”.
23.Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x)..Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:
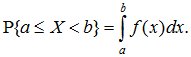
Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:
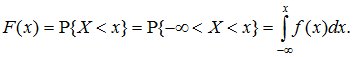
Равномерное распределение непрерывной случайной величины.

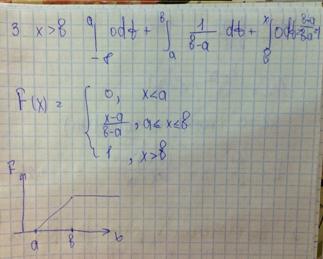
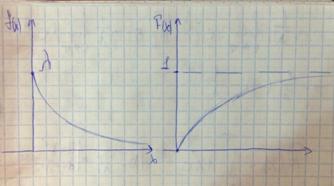
25.Показательное распределение непрерывной случайной величины.
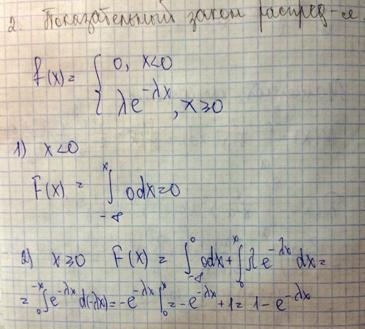
Нормальное распределение непрерывной случайной величины. Вычисление параметров распределения. Кривая Гаусса.
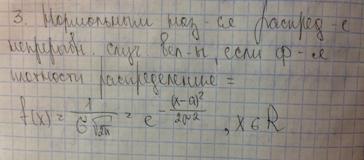
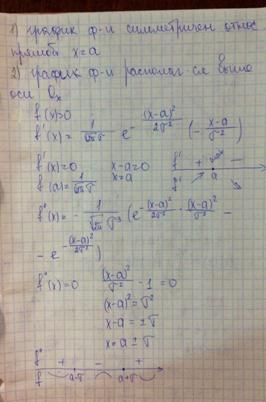
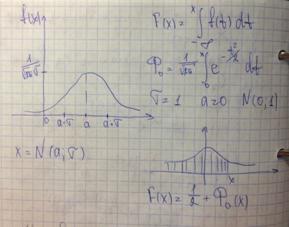
Правило трёх сигм.
и рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
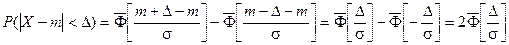
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
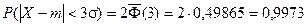
Закон больших чисел. Неравенство Чебышева.


29. Закон больших чисел (теорема Чебышева).

Закон больших чисел. Теорема Бернулли.


Понятие многомерной случайной величины


Понятие двумерной случайной величины и закон ее распределения.
Если на одном и том же пространстве элементарных событий заданы две случайные величины Х и Y, то это двумерная случайная величина (Х,Y).
Определение. Законом распределения дискретной двумерной случайной величины (Х,Y) называется таблица
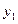 | 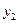 | … | 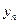 | |
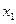 | 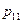 | 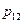 | 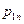 | |
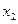 | 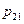 | 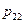 | 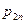 | |
| … | ||||
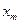 | 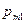 | 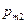 | 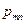 |
Здесь 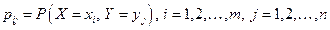 ;
; 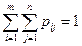 .
.
Для двумерной дискретной СВ