Характеристики выборочной совокупности
Определение 9.9. Выборочной средней называется сумма произведений всех вариант на соответствующие им частоты, делённая на сумму частот:
k
 ∑ xi ni
∑ xi ni
= =1 ,
где
k
n = ∑ ni .
i=1
xв i
n
Определение 9.10. Выборочной дисперсией называется величина,
определяемая по формуле:
| |
 ∑ ( xi
∑ ( xi
− xв ) ni
D = i =1 .
в n
Выборочная средняя и выборочная дисперсия являются точечными оценками соответствующих характеристик генеральной совокупности. То-
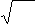 чечной оценкой среднего квадратического отклонения является σв =
чечной оценкой среднего квадратического отклонения является σв =
Dв .
Точечная оценка является приближённой, но не надёжной. Часто (осо- бенно при малом объёме выборки) в качестве точечной оценки дисперсии (среднего квадратического отклонения) генеральной совокупности исполь- зуют так называемую несмещённую, «исправленную» выборочную диспер-
сию s 2
(«исправленное» среднее квадратическое отклонение s ):
k

|
− x) 2 n
s 2 =
n D
 n − 1 в
n − 1 в
= i=1 .
n −1
Определение 9.11. Интервальной оценкой некоторого параметра называют числовой интервал, который покрывает неизвестное значение этого параметра с заданной вероятностью, называемой надёжностьюили доверительной вероятностью. Сам интервал при этом называется довери- тельным интервалом.
Пусть из генеральной совокупности, распределенной по нормальному закону, сделана выборка объёмом n .
 Доверительный интервал с надёжностью γ для генеральной средней xг
Доверительный интервал с надёжностью γ для генеральной средней xг
при известном среднем квадратическом отклонении σ :

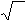


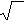 xв − t ⋅ σ /
xв − t ⋅ σ /
n ≤ xг ≤ xв + t ⋅ σ / n ,
где t определяется из условия ласа (приложение 2).
Φ(t ) = γ / 2
по таблице значений функции Лап-
Если же σ неизвестно и объём выборки невелик ( n < 30 ), то довери-
тельным интервалом служит интервал

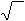


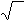 xв −tγ ⋅s/
xв −tγ ⋅s/
n ≤ xг ≤ xв +tγ ⋅s / n ,
где s – «исправленное» среднее квадратическое отклонение, tγ
определяется
|
(приложение 3).
=tкр.
(1 − γ; n −1)
Интервальной оценкой (с надёжностью γ ) среднего квадратического от-
клонения σ по «исправленному» выборочному среднему квадратическому
отклонению s служит интервал
s ⋅ (1 − q) <σ
< s ⋅ (1 + q)
(при
q <1),
0 <σ < s ⋅(1 + q)
(при
q >1),
 где q определяется по таблице приложения 4 по заданным γ и n .
где q определяется по таблице приложения 4 по заданным γ и n .
10 Уильям Сили Госсет (псевдоним – Стьюдент) (1876 – 1937) – английский математик.
Определение 9.12. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения. При этом проверяемую гипотезу называют нулевой, а гипотезу, которая противоречит нулевой гипотезе, называют альтернативнойили конкури- рующей.
При проверке статистической гипотезы может быть допущена одна из двух ошибок.
Ошибка первого рода состоит в том, что отвергается правильная нулевая гипотеза. Вероятность допустить ошибку первого рода называется уровнем
значимости критерия и обозначается через α .
Ошибка второго рода состоит в том, что принимается неправильная
нулевая гипотеза. Вероятность недопустить ошибку второго рода называется
мощностью критерия и обозначается через β .
Определение 9.13. Критерием согласия называется критерий про-
верки гипотезы о виде неизвестного распределения.
Пусть из генеральной совокупности сделана выборка достаточно боль- шого объёма n (не менее 50). Результаты выборки представлены в виде ин- тервального вариационного ряда (обычно при группировке вариант добива- ются того, чтобы в каждом интервале было не менее 5 вариант):
| ( x1 ; x2 ) | ( x2 ; x3 ) | … | ( xs ; xs +1 ) |
| n1 | n2 | ns |
Требуется на основании выборочных данных проверить гипотезу о том, что генеральная совокупность имеет нормальное распределение. Для решения этой задачи можно использовать критерий согласия Пирсона11.
 Алгоритм критерия согласия Пирсона
Алгоритм критерия согласия Пирсона
 1. Вычислить выборочную среднюю xв
1. Вычислить выборочную среднюю xв
и выборочное среднее квадратическое
отклонение
интервалов.
σв , при этом в качестве значений вариант взять середины
2. Определить теоретические частоты:
ni′ = n ⋅ pi
( i =1, ..., s ), где вероятности
 ⎛ x − x ⎞
⎛ x − x ⎞
⎛ x − x ⎞
pi находятся по формулам p
= Φ⎜ i +1 в⎟ − Φ⎜ i в⎟,
Φ(x)
– функция
Лапласа.
⎜ ⎟
|
⎜ ⎟
 ⎝ σв ⎠
⎝ σв ⎠
s 2

|
набл.
= ∑ (ni −ni′) .
n
i=1 i′
11 Карл Пирсон (1857 – 1936) – английский математик и биолог.
4. По таблице критических точек распределения
χ 2 (приложение 5) по за-
данному уровню значимости α и числу степеней свободы
k = s − 3
найти
|
кр.
(α; k ) .
5. Сравнить наблюдаемое и критическое значения критерия: если χ2
< χ2 ,
набл. кр.
то нет оснований отвергать гипотезу о нормальном распределении гене-
ральной совокупности; если же χ2
> χ2
– гипотеза отвергается.
набл. кр.
Пример 9.1. Имеются данные об объёме продаж оборудования:
| (75; 85) | (85; 95) | (95; 105) | (105; 115) | (115; 125) |
| |
α = 0,05
с помощью критерия согласия Пирсона про-
верьте гипотезу о том, что случайная величина X – объём продаж – имеет нормальное распределение.
Решение. Найдём выборочную среднюю и выборочное среднее квадра-
тическое отклонение, используя упрощенный метод ( с =100 ,
h =10 ):

|
|
Таким образом,
M1 = ∑ ui ni / n = −0,03 ,
M = ∑ u 2 n / n =1,15 ;
 xв = c + M 1 ⋅h =100 − 0,03 ⋅10 = 99,7 ;
xв = c + M 1 ⋅h =100 − 0,03 ⋅10 = 99,7 ;
| |
− M 2 ) ⋅ h 2
= (1,15 − (−0,03) 2 )⋅10 2
=114,91;
 σв =
σв =
114,91 =10,72 .
Теперь, исходя из предположения, что случайная величина X имеет
нормальное распределение с параметрами
a = 99,7
и σ =10,72, найдём веро-
ятность попадания случайной величины X в интервал (75; 85):
⎛ − ⎞ ⎛ − ⎞
 p = Φ⎜85
p = Φ⎜85
99,7⎟ − Φ⎜75
99,7 ⎟ = −0,4147+ 0,4893 = 0,075.
1 ⎝ 10,72 ⎠
⎝ 10,72 ⎠
Аналогично находятся вероятности попадания в другие интервалы.
|
 набл.
набл.
составим таблицу:
| Интервалы ( xi ; xi +1 ) | Эмпирические частоты ni | Вероятности pi | Теоретические частоты ni′ | (n − n′)2 i i ni′ |
| (75; 85) | 0,075 | 7,5 | 0,04 | |
| (85; 95) | 0,245 | 24,5 | 0,09 | |
| (95; 105) | 0,359 | 35,9 | ||
| (105; 115) | 0,234 | 23,4 | 0,24 | |
| (115; 125) | 0,068 | 6,8 | 0,74 | |
| ∑ | – | 1,11 |
|
χ 2 =1,11. Так как
|
< χ2 (0,05; 2) = 5,99
 (см. приложение 5),
(см. приложение 5),
то принимаем гипотезу о нормальном распределении величины X .
|
1. Что такое генеральная совокупность? выборочная совокупность?
2. Дайте определение вариационного ряда.
3. Как графически можно представить вариационный ряд?
4. Дайте определения основных характеристик выборки.
5. Как можно определить интервальные оценки характеристик генеральной совокупности по данным выборки?
6. Что называется критерием согласия?
7. Сформулируйте алгоритм критерия согласия Пирсона.
Задачи и упражнения
1. В 10 автосалонах Смоленска было соответственно продано автомобилей:
12, 10, 8, 15, 12, 12, 8, 10, 10, 12. а) Составьте вариационный ряд выборки.
б) Найдите эмпирическую функцию распределения выборки. в) Постройте полигон частот и относительных частот. г) Найдите выборочную среднюю
и выборочную дисперсию. д) Предполагая, что генеральная совокупность распределена по нормальному закону, определите доверительные интерва-
лы для генеральных средней и среднего квадратического отклонения с на-
дёжностью 0,95.
2. При исследовании деятельности банка были получены данные о статисти-
ческом распределении величины вкладов:
| Величина вклада, тыс. руб. | 10-20 | 20-30 | 30-40 | 40-50 |
| Количество вкладчиков |
а) Найдите эмпирическую функцию выборки. б) Постройте гистограмму относительных частот. в) Найдите выборочную среднюю и выборочное среднее квадратическое отклонение. г) Предполагая, что генеральная сово- купность распределена по нормальному закону, определите доверительные
интервалы для генеральных средней и среднего квадратического отклоне-
ния с надёжностью 0,95.
3. Получены данные о продолжительности 150 телефонных разговоров:
| Продолжительность тел. разговора, мин. | до 3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | более |
| Число разговоров |
а) С помощью критерия Пирсона проверьте на уровне значимости 0,05 ги- потезу о нормальном распределении продолжительности телефонного раз- говора. б) Определите границы, в которых с надежностью 0,95 заключёна длительность телефонного разговора. в) Каким должен быть объём вы- борки, чтобы те же границы гарантировать с надёжностью 0,99?
Домашнее задание
1. Компания не осуществляет инвестиционных вложений в ценные бумаги с дисперсией годовой доходности более чем 0,04. Выборка из 52 наблюде- ний по активу A показала, что выборочная дисперсия ее доходности равна
0,045. Выясните, допустимы ли для данной компании инвестиционные
вложения в актив A на уровне значимости: а) 0,05; б) 0,01.
2. Имеется следующее распределение жителей города по месячному доходу:
| Доход, тыс. руб. | менее 5 | 5-10 | 10-15 | 15-20 | более 20 |
| Количество жителей |
а) Проверьте на уровне значимости 0,05 гипотезу о нормальном распределе- нии дохода жителей города. б) Определите границы, в которых с надежно- стью 0,99 заключён средний месячный доход жителей города. в) Каким дол- жен быть объём выборки, чтобы те же границы гарантировать с надёжностью
0,9973?
Занятие 10. Методы шкалирования. Статистический анализ количественных и качественных признаков
На практике не всегда приходится иметь дело с переменными, измеренными в количественных шкалах, т.е. в шкалах с непрерывным множеством значений, позволяющих определять, насколько проявление признака у одного объекта больше (меньше), чем у другого.
Наряду с количественными шкалами встречаются также порядковые и номинальные шкалы.
Определение 10.1. Шкала называется порядковой, если в ней установлен лишь порядок значений, однако с этими значениями нельзя проводить никаких арифметических действий.
Определение 10.2. Шкала называется номинальной, если её значе- ния нельзя ни сравнивать между собой, ни производить над ними какие-либо арифметические действия.
Определение 10.3. Признаки, измеренные в порядковой или номи-
нальной шкале, называются качественными.
Существует большое разнообразие статистических методов анализа ка-
чественных признаков – методы непараметрической статистики. К ним отно-
сятся критерий
χ2 , ранговая корреляция.
Допустим, что объекты генеральной совокупности исследуются на нали- чие взаимосвязи двух признаков X и Y , причём эти признаки могут быть как количественными, так и качественными.
Пусть признаки X и Y имеют конечное число значений
A1 , A2 , ..., Ap и
B1 , B2 , ..., Bl
соответственно.
 Из генеральной совокупности сделана выборка объемом n . Результаты этой выборки занесены в таблицу сопряжённостей:
Из генеральной совокупности сделана выборка объемом n . Результаты этой выборки занесены в таблицу сопряжённостей:
где
|
p
= ∑ nij ;
i =1
•1 •2 •l
l
ni • = ∑ nij .
j =1
Требуется на уровне значимости α проверить гипотезу
в том, что признаки X и Y независимы.
H 0 , состоящую
Для решения этой задачи можно использовать критерий χ2
(хи-квадрат).
Алгоритм критерияχ 2
|
набл.
по формуле:
 p l (n
p l (n
− n′ )2
|
набл.
=∑∑
i=1 j =1
ij ij ,
ni′j
где
nij – эмпирические частоты,
ni′j
– теоретические частоты, которые на-
ходятся по формуле n′
= ni•
n• j .
 ij n
ij n
2. По таблице приложения 5 определить критическое значение критерия
|
кр.
= χ2 (α; ( p −1)(l −1))
по заданным уровню значимости α и числу сте-
пеней свободы
k = ( p −1)(l −1) .
3. Сравнить наблюдаемое и критическое значения критерия: если χ2
< χ2 ,
то гипотезу
набл. кр.
H 0 о независимости признаков X и Y принять. В противном
случае – отклонить: признаки X и Y зависимы.
 Пример 10.1. Исследовалась зависимость между двумя признаками: X – название фирмы, где производилось изделие, и Y – возраст покупателя этих изделий. Результаты выборки приведены в таблице.
Пример 10.1. Исследовалась зависимость между двумя признаками: X – название фирмы, где производилось изделие, и Y – возраст покупателя этих изделий. Результаты выборки приведены в таблице.
| Y X | До 30 лет | 30 – 50 лет | Свыше 50 лет | ni• |
| Фирма № 1 | ||||
| Фирма № 2 | ||||
| Фирма № 3 | ||||
| n• j |
Проверьте на уровне значимости
ков X и Y .
α = 0,01
гипотезу о независимости призна-
Решение. Составим матрицу теоретических частот
ni′. Получим

 ⎛38 ⋅39
⎛38 ⋅39
⎜
50 ⋅39
22 ⋅39 ⎞
⎟
⎜ 110
 38 ⋅ 37
38 ⋅ 37

 50 ⋅37
50 ⋅37
110 ⎟

 22 ⋅ 37
22 ⋅ 37
⎛13,5
⎜
17,7
7,8 ⎞
⎟
P′ = ⎜
⎟ = ⎜12,8
16,8
7,4 ⎟.
 ⎜ 110
⎜ 110
110 ⎟ ⎜ ⎟
⎜38 ⋅ 34
⎜
50 ⋅ 34
22 ⋅ 34 ⎟
|
⎝11,7
15,5
6,8 ⎠
⎝ 110
110 ⎠
Найдем наблюдаемое значение критерия:
набл.
= 24,7.
По таблице критических точек распределения
χ2 (приложение 5) нахо-
дим
кр.
(0,01; 4) = 13,3 .
|
> χ 2
, то гипотезу
H о независимости признаков откло-
набл. кр. 0
няем. Значит, признаки X и Y зависимы.
Замечание. Величина χ2
неудобна как величина, оценивающая тесно-
ту связи признаков, так как она зависит от объема выборки n . Поэтому в ка- честве величин, которые позволяют оценить тесноту связи, часто используют следующие показатели сопряженности:
показатель Пирсона: C =
a ,
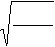 n + a
n + a
показатель Крамера12: c =
a ,
 n⋅ min( p −1; l −1)
n⋅ min( p −1; l −1)
показатель Чупрова13: c =
a ,
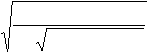 n ⋅ ( p − 1)( l − 1)
n ⋅ ( p − 1)( l − 1)
⎛ p l 2

|
⎞
1⎟.
где
= ⎜∑∑ n n − ⎟
⎝ i=1 j =1
i• • j ⎠
Значения этих показателей заключены в отрезке [0; 1] , причем чем ближе
показатель к 1, тем связь между изучаемыми признаками сильнее.
В случае, если признаки X и Y порядковые, то для оценки их связи час-
то используют коэффициенты ранговой корреляции Спирмена14 и Кендалла15.
Рассмотрим теперь выборку объема n , содержащую независимые объек-
ты, обладающие двумя порядковыми признаками A и B .
