Каноническое уравнение параболы.

Определение 1. Параболойназывается множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом,и от данной прямой, не проходящей через данную точку и называемой директрисой.

Составим уравнение параболы с фокусом в данной точке F и директрисой которой является прямая d, не проходящая через F. Выберем прямоугольную систему координат следующим образом: ось Ох проведем через фокус F перпендикулярно директрисе d в направлении от d к F, а начало координат О расположим посередине между фокусом и директрисой (рис. 1).

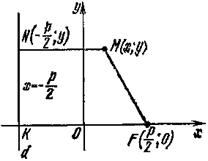
Рис. 1

Определение 2. Расстояние от фокуса F до директрисы d называется параметром параболыи обозначается через р (р > 0).

Из рис. 1 видно, что p = FK, следовательно, фокус имеет координаты F (р/2; 0), а уравнение директрисы имеет вид х = – р/2, или

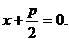
Пусть М(х; у) – произвольная точка параболы. Соединим точку М с F ипроведем MN 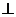d. Непосредственно из рис. 1 видно, что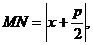

а по формуле расстояния между двумя точками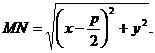

Согласно определению параболы, MF = MN, (1)

следовательно, 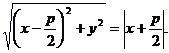(2)

Уравнение (2) является искомым уравнением параболы. Для упрощения уравнения (2) преобразуем его следующим образом:

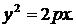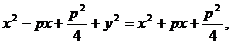т.е.,

(3)

Координаты х и у точки М параболы удовлетворяют условию (1), а следовательно, и уравнению (3).

Определение 3. Уравнение (3) называется каноническим уравнением параболы.

2. Исследование формы параболы по ее уравнению. Определим форму параболы по ее каноническому уравнению (3).

1) Координаты точки О (0; 0) удовлетворяют уравнению (3), следовательно, парабола, определяемая этим уравнением, проходит через начало координат.

2) Так как в уравнение (3) переменная у входит только в четной степени, то парабола у² = 2рх симметрична относительно оси абсцисс.

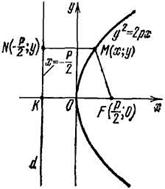
Рис. 2.

3) Так как р > 0, то из (3) следует х ≥ 0. Следовательно, парабола у² = 2рх расположена справа от оси Оу.

4) При возрастании абсциссы х от 0 до +∞ ордината у изменяется от 0 до ±∞, т.е. точки параболы неограниченно удаляются как от оси Ох, так и от оси Оу.

Парабола у² = 2рх имеет форму, изображенную на рис. 2.

Определение 4. Ось Ох называется осью симметрии параболы. Точка О (0; 0) пересечения параболы с осью симметрии называется вершиной параболы. Отрезок FM называется фокальным радиусом точки М.

Замечание. Для составления уравнения параболы вида у² = 2рх мы специальным образом выбрали прямоугольную систему координат (см. п. 1). Если же систему координат выбрать другим образом, то и уравнение параболы будет иметь иной вид.

а

б в

Рис. 3

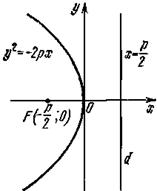
Так, например, если направить ось Ох от фокуса к директрисе (рис. 3, а), то уравнение параболы примет вид

у² = –2рх. (4)

Фокус такой параболы имеет координаты F(–р/2; 0), а директриса d задана уравнением х = р/2.

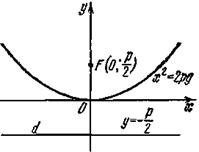
Если ось Оу проведем через фокус F перпендикулярно к директрисе d в направлении от d к F, а начало координат О расположим посередине между фокусом и директрисой (рис. 3, б), то уравнение параболы пример вид

х² = 2ру.(5)

Фокус такой параболы имеет координаты F (0; р/2), а директриса d задана уравнением у=–р/2.

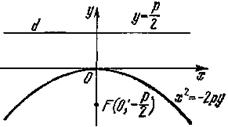
Если ось Оу проведем через фокус F перпендикулярно к директрисе d в направлении от F к d (рис. 3, в), то уравнение параболы примет вид

х² = –2ру (6)

Координаты ее фокуса будут F (0; –р/2), а уравнением директрисы d будет у = р/2.

Об уравнения (4), (5), (6) говорят, что они имеют простейший вид.

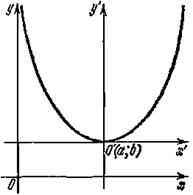
Рис. 4

3. Параллельный перенос параболы. Пусть дана парабола с вершиной в точке О' (а; b), ось симметрии которой параллельна оси Оу, а ветви направлены вверх (рис. 4). Требуется составить уравнение параболы.

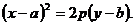(9)

Определение 5. Уравнение (9) называется уравнением параболы со смещенной вершиной.

Преобразуем это уравнение следующим образом:

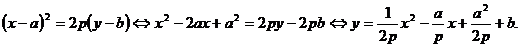
Положив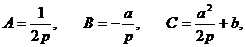

будем иметь 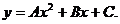(10)

Нетрудно показать, что для любых А, В, С график квадратного трехчлена (10) представляет собой параболу в смысле определения 1. Уравнение параболы вида (10) изучалось в школьном курсе алгебре.

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

№1. Составить уравнение окружности:

a. с центром в начале координат и радиусом 7;

b. с центром в точке (-1;4) и радиусом 2.

Построить данные окружности в прямоугольной декартовой системе координат.

№2. Составить каноническое уравнение эллипса с вершинами

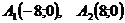и фокусами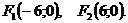

№3. Построить эллипс, заданный каноническим уравнением:

1) 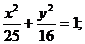2)

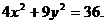
№4. Составить каноническое уравнение эллипса с вершинами

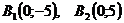и фокусами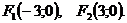

№5. Составить каноническое уравнение гиперболы с вершинами

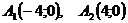и фокусами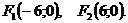

№6. Составить каноническое уравнение гиперболы, если:

1. расстояние между фокусами 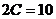, а между вершинами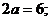

2. действительная полуось 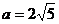, а эксцентриситет ;

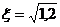3. фокусы на оси 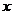, действительная ось 12, а мнимая 8.

№7. Построить гиперболу, заданную каноническим уравнением:

1) 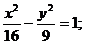2) .

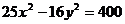№8. Составить каноническое уравнение параболы, если:

1) парабола расположена в правой полуплоскости симметрично относительно оси 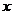и её параметр ;

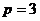2) парабола расположена в левой полуплоскости симметрично относительно оси и её параметр .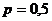

Построить эти параболы, их фокусы и директрисы.

№9. Определить тип линии, если её уравнение:

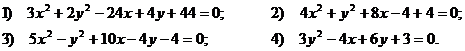
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Векторы в пространстве.

1.1. Что такое вектор?

1.2. Что такое абсолютная величина вектора?

1.3. Какие виды векторов в пространстве Вы знаете?

1.4. Какие действия можно выполнять с ними?

1.5. Что такое координаты вектора? Как их найти?

2. Действия над векторами, заданными своими координатами.

2.1. Какие действия можно выполнять с векторами, заданными в координатной форме (правила, равенства, примеры); как найти абсолютную величину такого вектора.

2.2. Свойства:

2.2.1 коллинеарных;

2.2.2 перпендикулярных;

2.2.3 компланарных;

2.2.4 равных векторов.
(формулировки, равенства).

3. Уравнение прямой. Прикладные задачи.

3.1. Какие виды уравнения прямой Вы знаете (уметь записывать и интерпретировать по записи);

3.2. Как исследовать на параллельность – перпендикулярность две прямые, заданные уравнениями с угловым коэффициентом или общими уравнениями?

3.3. Как найти расстояние от точки до прямой, между двумя точками?

3.4. Как найти угол между прямыми, заданными общими уравнениями прямой или уравнениями с угловым коэффициентом?

3.5. Как найти координаты середины отрезка и длину этого отрезка?

4. Уравнение плоскости. Прикладные задачи.

4.1. Какие виды уравнения плоскости Вы знаете (уметь записывать и интерпретировать по записи)?

4.2. Как исследовать на параллельность – перпендикулярность прямые в пространстве?

4.3. Как найти расстояние от точки до плоскости и угол между плоскостям?.

4.4. Как исследовать взаимное расположение прямой и плоскости в пространстве?

4.5. Виды уравнения прямой в пространстве: общее, каноническое, параметрическое, проходящей через две данные точки.

4.6. Как найти угол между прямыми и расстояние между точками в пространстве?

5. Линии второго порядка.

5.1. Эллипс: определение, фокусы, вершины, большая и малая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения эллипса; чертеж.

5.2. Гипербола: определение, фокусы, вершины, действительная и мнимая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения гиперболы; чертеж.

5.3. Парабола: определение, фокус, директриса, вершина, параметр, ось симметрии, простейшие (или канонические) уравнения параболы; чертеж.

Примечание к 4.1, 4.2, 4.3: Для каждой линии 2го порядка уметь описывать построение.

ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ

1.Даны точки: 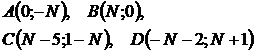, где N – номер студента по списку.

1. Найти координаты, абсолютные величины и направляющие косинусы векторов .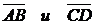

2. При каком значении числа 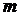перпендикулярны векторы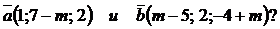

3. Проверить, коллинеарны ли векторы ?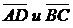

4. Образуют ли векторы 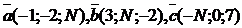базис?

5. Найти угол между векторами .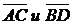

6. Образуют ли векторы 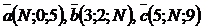базис? Если да, найти в нем координаты вектора .

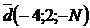2.Даны координаты вершин треугольника A, B, C (сделать чертеж). Найти:

1) уравнение стороны AB;

2) уравнение медианы AF;

3) уравнение высоты CK;

4) длины сторон треугольника и высоты CK;

5) косинус угла ABC.

1. A (-3; 2), B (0; 14), C (6; 6).

2. A (-3; -1), B (0; 13), C (6; 5).

3. A (6; 2), B (9; 14), C (15; 6).

4. A (-1; -1), B (2; 11), C (8; 3).

5. A (11; -2), B (10; 10), C (16; 2).

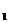
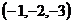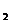
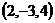3. Даны четыре точки М , М 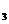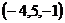, М , М 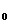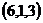. Требуется:

1) написать уравнение плоскости Р, проходящей через точки 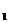М 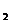, М , М ;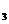

2) преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить эту плоскость;

3) найти расстояние от точки М 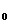до плоскости Р.

4. Построить линию второго порядка, заданную своим каноническим уравнением:

.

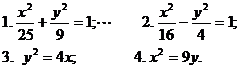ЛИТЕРАТУРА

1.Высшая математика для экономистов - Учебник для вузов под ред. Н.Ш. Кремер и др., - Москва, ЮНИТИ, 2003.

2.Барковський В.В., Барковська Н.В. - Вища математика для економістів – Київ, ЦУЛ, 2002.

3.Суворов И.Ф. - Курс высшей математики. - М., Высшая школа, 1967.

4.Тарасов Н.П. - Курс высшей математики для техникумов. - М.; Наука, 1969.

5.Зайцев И.Л. - Элементы высшей математики для техникумов. - М.; Наука, 1965.

6.Валуцэ Н.Н., Дилигул Г.Д. - Математика для техникумов. - М.; Наука, 1990.

7.Шипачев В.С. - Высшая математика. Учебник для вузов – М.: Высшая школа, 2003.