Исследование формы гиперболы по ее уравнению.

Определим форму гиперболы по ее каноническому урав­нению (4).

1) Координаты точки О (0; 0) не удовлетворяют уравнению (4), поэтому гипербола, определяемая этим уравнением, не проходит через начало координат.

2) Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (4) у = 0, найдем х = ± а. Следовательно, гипербола пересекает ось Ох в точках A₁ (a; 0) и А₂ (–а; 0). Положив в уравнении (4) х = 0, получим у² = – b², а это означает, что система

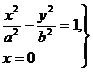
не имеет действительных решений. Следовательно, гипербола не пересекает ось Оу.

3) Так как в уравнение (4) переменные х и у входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.

4) Определим область изменения переменных х и у;для этого из уравнения (4) находим

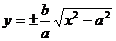, (5)

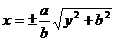. (6)

Из (5) следует, что |х| ≥ а, т.е. х ≥ а или х ≤ –а; из (6) следует, что у – любое действительное число. Таким образом, все точки гиперболы расположены слева oт прямой х = – а и справа от прямой х = а.

5) Из (5) следует также, что

у → ± ∞ при х → + ∞.

у → ± ∞ при х → – ∞.

Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой х = а (правая ветвь гиперболы), а другая – слева от прямой х = – а (левая ветвь гиперболы).

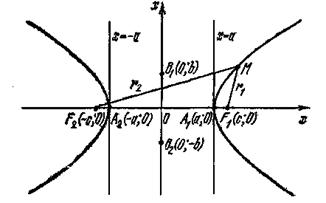
Рис. 2

Гипербола имеет форму, изображенную на рис. 2.

Определение 4. Точки А₁ (а; 0) и А₂ (а; 0) пересечения гиперболы с осью Ох называются вершинами гиперболы. Отрезок A₁A₂ (A₁A₂=2a),соединяющий вершины гиперболы, называется действительной осью.Отрезок B₁B₂ (B₁B₂=2b), соединяющий точки B₁ (0; b) и В₂ (0; –b), называется мнимой осью.Число а называется действительной полуосью, число b – мнимой полуосью.Оси А₁А₂ и В₁В₂ являются осями симметрии гиперболы. Точка О пересечения осей симметрии называется центром гиперболы.

У гиперболы (4) фокусы F₁ и F₂ всегда находятся на действительной оси.

Можно показать (так же, как и в случае эллипса), что фокальные радиусы для точки М (х; у), расположенной на правой ветви гиперболы, вычисляются по формулам

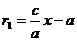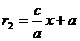и , (7)

а для точки М (х; у), расположенной на левой ветви, – по формулам

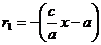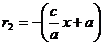и . (8)

Асимптоты гиперболы.

Определение 5. Прямая y=kx+m называется наклонной асимптотойкривой y = f(x) при х → +∞,если

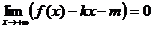. (9)

Аналогично определяется асимптота при х → –∞. Докажем, что прямые

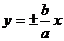(10)

являются асимптотами гиперболы (4) при х → ±∞.

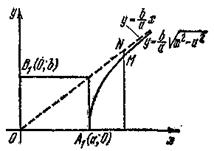
Рис. 3

Так как прямые (10) и гипербола (4) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 3). Напишем уравнения прямых (10) и гиперболы (4), соответствующие первой четверти:

,

.

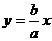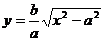Положив 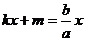и 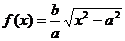, найдем

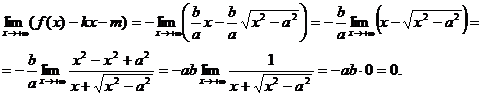
Следовательно, прямые (10) являются асимптотами гиперболы (4).

Отметим, что асимптоты (10) являются продолжениями диагоналей прямоугольника, стороны которого параллельны осям Ох и Оу и равны соответственно 2а и 2b, а его центр находится в начале координат.

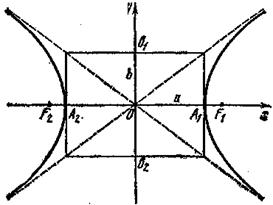
Рис. 4

При этом ветви гиперболы расположены внутри вертикальных углов, образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис. 4).

Эксцентриситет гиперболы.

Определение 6. Эксцентриситетом гиперболыназывается отношение расстояния между фокусами к длине действительной оси и обозначается буквой ε:

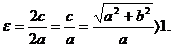(11)

5. Сопряженная гипербола. Рассмотрим уравнение вида

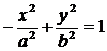. (12)

При переходе к новой системе координат, полученной в результате поворота осей старой системы вокруг начала координат на угол α = 90° (или α = –90°), уравнение (12) преобразуется в уравнение гиперболы

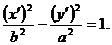
Следовательно, кривая, определяемая уравнением (12), есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а – на оси Ох.

Две гиперболы, которые определяются уравнениям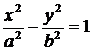и

и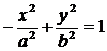

в одной и той же системе координат и при одних и тех же значениях а и b, называются сопряженнымидруг с другом.

Равносторонняя гипербола.

Определение 7. Гипербола называется равносторонней,если длины ее полуосей равны между собой, т.е. а=b. В этом случае уравнение гиперболы принимает вид

,

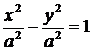или

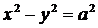. (13)

Равносторонняя гипербола определяется одним параметром а и асимптотами являются биссектрисы координатных углов

.

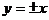У всех равносторонних гипербол один и тот же эксцентриситет

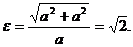
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат Ox'y', полученной в результате поворота осей старой системы вокруг начала координат на угол α = –45° (рис. 5). Составим уравнение равносторонней гиперболы относительно новой системы координат Ох'у'.

Учитывая равенство (13), получим x'y' = а²/2. (14)

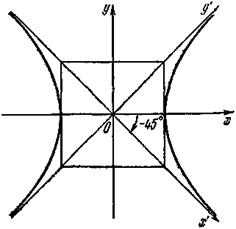
Рис. 5

Определение 8. Уравнение (14) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.

Из уравнения (14) следует, что переменные х' и у' – величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратной пропорциональной зависимости.

Если центр гиперболы находится не в начале координат, а в точке О'(х₀; у₀), а оси гиперболы параллельны осям координат, то уравнение гиперболы будет иметь вид

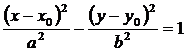
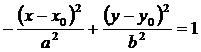или (15)

Это уравнения гиперболы со смещенным центром.

«Парабола»