Совокупность каких-либо n векторов, взятых из системы векторов ранга n, образующая линейно независимую систему, называется базисом исходной системы векторов.
Учитывая это определение, из ранее рассмотренного следует справедливость следующих утверждений:
1. Любая пара неколлинеарных векторов системы векторов на плоскости может быть взята как базис этой системы, т.е., если 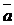 и
и 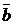 - неколлинеарны и взяты как базис этой системы векторов на плоскости, то любой вектор
- неколлинеарны и взяты как базис этой системы векторов на плоскости, то любой вектор 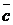 этой системы может быть выражен через выбранный базис равенством:
этой системы может быть выражен через выбранный базис равенством: 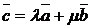
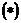 , где
, где 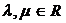 - координаты вектора
- координаты вектора 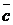 относительно базиса
относительно базиса 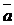 и
и 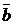 , т.е.
, т.е. 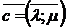
2. Любая тройка некомпланарных векторов системы векторов в пространстве может быть взята как базис этой системы, т.е., если 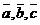 - некомпланарны и взяты как базис системы векторов в пространстве, то любой вектор
- некомпланарны и взяты как базис системы векторов в пространстве, то любой вектор 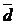 этой системы может быть выражен через выбранный базис равенством:
этой системы может быть выражен через выбранный базис равенством: 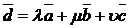
 , где
, где 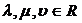 - координаты вектора
- координаты вектора 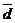 относительно базиса
относительно базиса 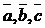 , т.е.
, т.е. 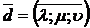 .
.
Равенства 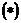 и
и  называются формулами разложения векторов системы по выбранным базисным векторам.
называются формулами разложения векторов системы по выбранным базисным векторам.
Выбор базиса дает возможность однозначно поставить в соответствие каждому вектору системы упорядоченный набор чисел – координат вектора в выбранном базисе. И наоборот, каждому упорядоченному набору чисел в некотором базисе однозначно соответствует некоторый вектор.
Замечания: 1. Наиболее рационально выбирать в виде базиса орты 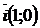 и
и 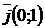 на плоскости и орты
на плоскости и орты 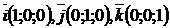 в пространстве, т.е., разложение в этих случаях имеет вид:
в пространстве, т.е., разложение в этих случаях имеет вид:
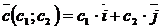
или 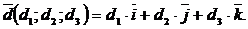
2. Чтобы проверить линейную независимость векторов 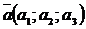 ,
,
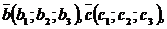 надо составить определитель из координат этих векторов и найти его значение. Если
надо составить определитель из координат этих векторов и найти его значение. Если 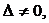 векторы линейно независимы и образуют базис. Иначе, эти векторы называют компланарными.
векторы линейно независимы и образуют базис. Иначе, эти векторы называют компланарными.
3.Чтобы найти координаты вектора 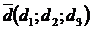 в данном базисе
в данном базисе 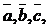 т.е., если выполняется равенство
т.е., если выполняется равенство 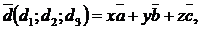 необходимо составить систему уравнений относительно переменных x,y,z:
необходимо составить систему уравнений относительно переменных x,y,z:
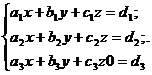
и решить эту систему уравнений любым из известных методов.
Найденные значения переменных x,y,z есть координаты вектора 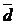 в базисе
в базисе 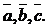
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
№ 1 а) Длина вектора на плоскости находится по одной из формул:
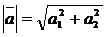 , где
, где 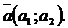 .
.
или 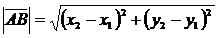 , где
, где 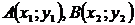 .
.
Найти длину вектора:
1) 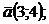 2)
2) 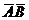 , где
, где 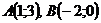 .
.
б) Длина вектора в пространстве находится по одной из формул:
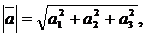 где
где 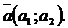
или 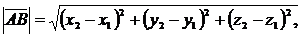 где
где 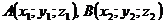 .
.
Найти длину вектора:
1) 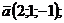 2)
2) 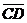 , где
, где 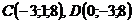 .
.
№ 2 Направляющими косинусами вектора 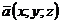 называются числа
называются числа 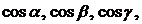 где
где
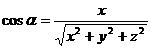 ;
; 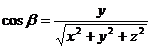 ;
; 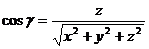 .
.
Найти длину вектора 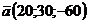 и его направляющие косинусы.
и его направляющие косинусы.
№ 3 Скалярным произведением векторов 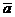 и
и 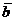 называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними:
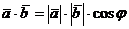 .
.
Если векторы заданы в координатной форме, то скалярное произведение находят по формуле:
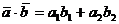 , если
, если 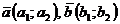
или 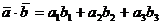 , если
, если 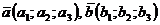
Найти скалярное произведение векторов:
1) 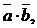 если
если 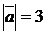 ,
, 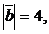
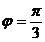 .
.
2) 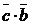 , если
, если 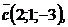
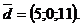
№ 4 Для нахождения угла между векторами используют одну из формул:
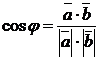 или
или 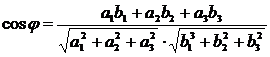 или
или
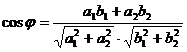
Найти угол между векторами:
1) 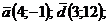
2) 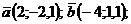
3) 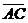 и
и 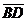 где А(6;-2), В(-4;8), С(0;-4), D(6;0).
где А(6;-2), В(-4;8), С(0;-4), D(6;0).
№ 5 Правило умножения вектора на число:
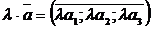 .
.
Правило сложения векторов:
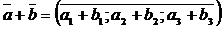
Выполнить действия: 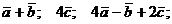
где 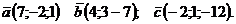
№ 6 Базисом 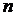 - мерного пространства
- мерного пространства 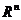 называют множество
называют множество 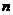 линейно независимых векторов
линейно независимых векторов 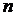 - мерного пространства. Векторы
- мерного пространства. Векторы 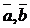 и
и 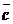 линейно независимы, если определитель, составленный из их координат, отличен от нуля:
линейно независимы, если определитель, составленный из их координат, отличен от нуля:
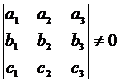
Разложить вектор 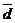 по базису – значит представить этот вектор как линейную комбинацию базисных векторов:
по базису – значит представить этот вектор как линейную комбинацию базисных векторов: 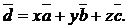
Для нахождения неизвестных чисел 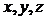 необходимо составить систему линейных алгебраических уравнений и решить ее любым способом.
необходимо составить систему линейных алгебраических уравнений и решить ее любым способом.
Проверить, составляют ли векторы 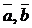 и
и 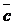 базис в пространстве R3 и найти координаты вектора
базис в пространстве R3 и найти координаты вектора 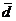 в этом базисе:
в этом базисе:
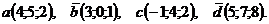
№ 7 Два вектора 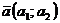 и
и 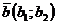 или
или 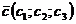 и
и 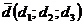 перпендикулярны, если их скалярное произведение равно 0.
перпендикулярны, если их скалярное произведение равно 0.
а) Перпендикулярны ли векторы:
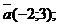
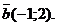
б) При каком х перпендикулярны векторы 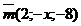 и
и 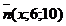 ?
?
№ 8 Два вектора 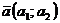 и
и 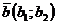 или
или 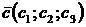 и
и 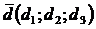 коллинеарны, если их соответствующие координаты пропорциональны, т.е.
коллинеарны, если их соответствующие координаты пропорциональны, т.е. 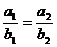 или
или 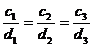 .
.
а) Коллинеарны ли векторы
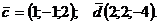
б) При каком m коллинеарны векторы 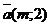 и
и 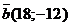 ?
?
