Лабораторная работа №2. Исследование устойчивости линейных САУ

Содержание работы

Для расчета систем автоматического управления (САУ) они разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида, но описываемое определенным дифференциальным уравнением. В соответствии с этим звенья классифицируются именно по виду дифференциального уравнения, или что то же, по виду передаточной функции звена. Под типовым звеном понимается звено, описываемое дифференциальным уравнением не выше второго порядка:

.

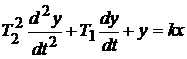При нулевых начальных условиях (т.е. если для t<0 входная и выходная величины, а также их производные тождественно равны нулю) передаточная функция звена может быть найдена как отношение изображений по Лапласу выходной и входной величин

,

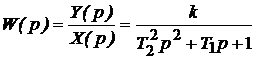где p=c+jω– комплексная величина.

При известной передаточной функции звена изображение по Лапласу его выходной величины можно найти из выражения

.

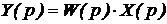Динамические свойства звена определяются по его временным и частотным характеристикам. Наиболее распространенными временными характеристиками являются переходная характеристика и функция веса.

Переходная функция, или переходная характеристика h(t), представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход единичного скачкообразного воздействия (рис. 1,а). Такое входное воздействие называется единичной ступенчатой функцией (рис. 1,б):

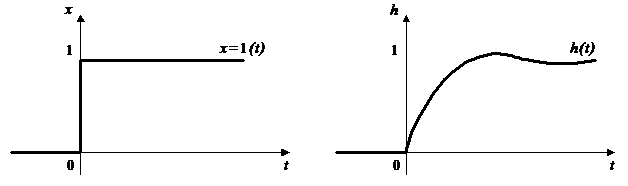а) б)

Рис.1. Переходная функция:

а - единичное скачкообразное воздействие 1(t); б – переходная характеристика h(t)

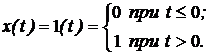
Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию (рис. 2,а). Единичная импульсная функция, или дельта-функция (рис. 2,б), представляет собой производную от единичной ступенчатой функции

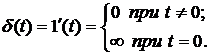
Основное свойство дельта функции заключается в том, что 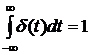, т.е. она имеет единичную площадь.

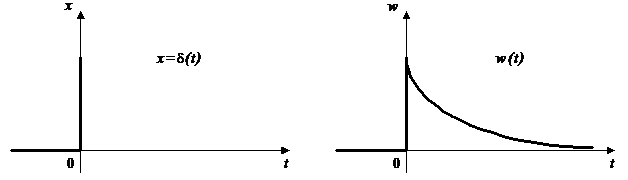а) б)

Рис.2. Функция веса:

а - единичный импульс d(t); б – функция веса w(t)

При описании линейных систем или звеньев важное значение имеют частотные характеристики. Они описывают установившиеся вынужденные колебания в системе при подаче на ее вход гармонического воздействия. В общем случае уравнение линейной системы можно записать так:

.

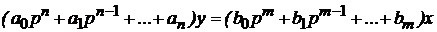Ее передаточная функция имеет вид

.

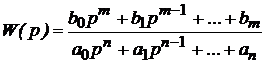Функцию W(jw), которую получают из передаточной функции W(p) при подстановке в нее p=jw, называют частотной передаточной функцией

.

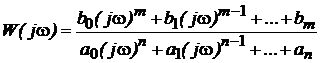Частотная передаточная функция является комплексной функцией от действительной переменной w, которая называется частотой.

Функцию W(jw) можно представить в виде

,

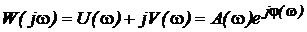где

.

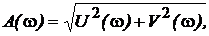
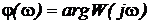Если 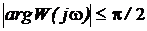, то .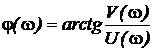

На комплексной плоскости частотная передаточная функция W(jw) определяет вектор, длина которого равна A(w), а аргумент, т.е. угол, образованный этим вектором с действительной положительной полуосью - j(w). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ¥ (иногда от -¥ до ¥), называют амплитудно-фазовой частотной характеристикой (АФЧХ).

Модуль 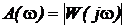называют амплитудной частотной функцией, а ее график – амплитудной частотной характеристикой.

Аргумент 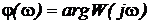называют фазовой частотной функцией, а ее график фазовой частотной характеристикой.

Кроме перечисленных частотных характеристик, используют еще логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ). При построении графиков этих характеристик по оси абсцисс откладывают логарифм частоты lgw. Единицей логарифма частоты является декада. Декадой называется интервал, на котором частота изменяется в 10 раз. Для графика ЛАЧХ по оси ординат откладывается функция 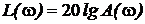, а для графика ЛФЧХ – функцию 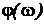. Ось ординат проводят через произвольную точку, а не через точку w=0, так как lgw ® - ¥ при w ® 0. Пример графиков ЛЧХ приведен на рис.3. Основные типовые звенья САУ приведены в табл. 1.

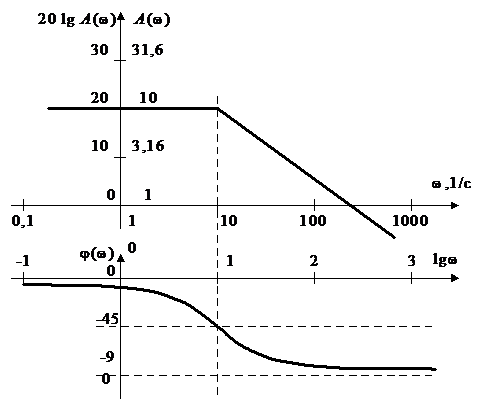
Рис.3. Логарифмические частотные характеристики

Порядок выполнения работы

1. Набрать модель звена.

2. Получить семейства графиков переходных характеристик звена при изменении:

- коэффициента передачи K=1…10;

- постоянных времени звена T=0,1…1;

- коэффициента демпфирования x=0,1…1.

3. По полученным графикам определить основные показатели переходных характеристик:

- величину установившегося значения h_уст;

- длительность переходного процесса t_пер;

- перерегулирование s ( ).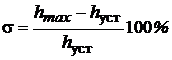

4. Получить семейства графиков частотных характеристик звена (АФЧХ, ЛАЧХ, ФЧХ) при параметрах, указанных в п.2.

5. Провести сравнительный анализ полученных характеристик, сделать выводы о влиянии параметров передаточных функций звеньев на их динамические характеристики.

Таблица 1

Основные типовые звенья САУ

Позиционные
1. Безинерционное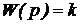
2. Апериодическое первого порядка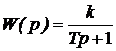
3. Апериодическое второго порядка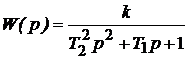
4. Колебательное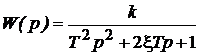
5. Консервативное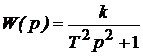
Интегрирующие
1. Идеальное интегрирующее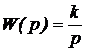
2. Интегрирующее с замедлением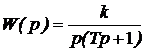
3. Изодромное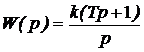
Дифференцирующие
1. Идеальное дифференцирующее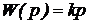
2. Дифференцирующее с замедлением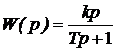

3. Контрольные вопросы

1. Какие временные характеристики САУ вы знаете и какова их связь с передаточными функциями САУ?

2. Какие виды частотных характеристик САУ вам известны и какой их физический смысл?

3. Какие типовые динамические звенья вы знаете, их передаточные функции и дифференциальные уравнения?

4. Как влияют параметры передаточных функций звеньев на их временные и частотные характеристики?

5. Каким образом выполняется расчет переходного процесса на выходе звена при произвольном входном воздействии по переходной и импульсной характеристикам?

6. Как получить частотные характеристики звеньев по их передаточным функциям?

7. Как строятся логарифмические частотные характеристики?

Ход работы:

1. Набираем модель идеального дифференцирующего звена в программе Matlab

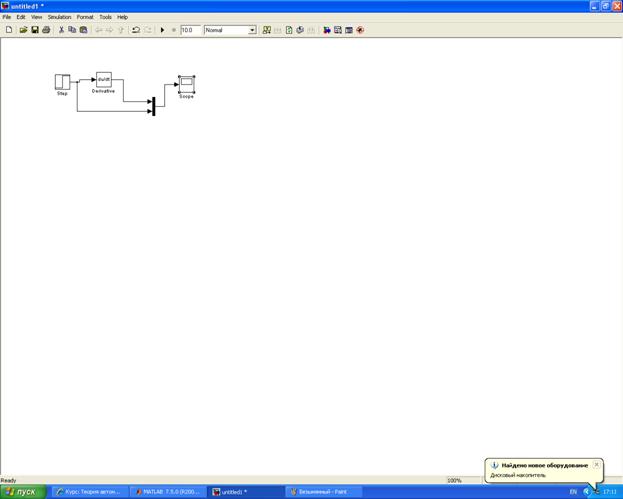
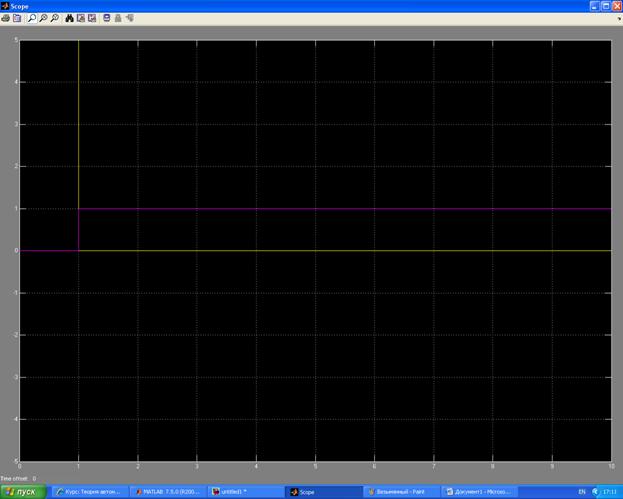
2. По показаниям осциллографа получаем следующие частотные характеристики

Цель работы

Исследовать замкнутую систему автоматического управления (ЗСАУ) при помощи критериев устойчивости Гурвица, Михайлова и Найквиста. Применить в работе ПО MATLAB.

Программа работы

1. Реализовать систему согласно следующим данным:

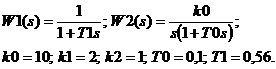
Структурная схема системы представлена на рисунке 1.

2. Проверить систему на устойчивость по алгебраическому критерию Гурвица. Сделать выводы.

3. Определить устойчивость системы по корням. Сделать выводы.

4. Изучить в MATLAB Help функции ltiview и margin и с их помощью получить информацию о переходной характеристике и оценить запас устойчивости.

5. Проверить систему на устойчивость по частотному критерию Михайлова. Сделать выводы.

6. Проверить систему на устойчивость по частотному критерию Найквиста. Сделать выводы.

Ход работы

Реализация системы

Передаточные функции звеньев САУ, представленной на рисунке (1), а также разомкнутой и замкнутой систем запишем в общем виде:

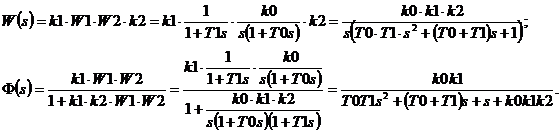
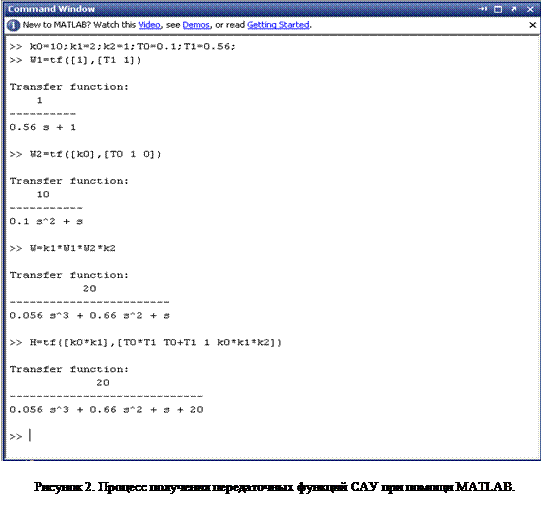
На рисунке 2 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения параметров САУ, а на рисунке 3 – представление ее в виде модели в пространстве состояний.

Содержание работы

Для расчета систем автоматического управления (САУ) они разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида, но описываемое определенным дифференциальным уравнением. В соответствии с этим звенья классифицируются именно по виду дифференциального уравнения, или что то же, по виду передаточной функции звена. Под типовым звеном понимается звено, описываемое дифференциальным уравнением не выше второго порядка:

.

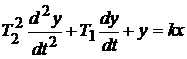При нулевых начальных условиях (т.е. если для t<0 входная и выходная величины, а также их производные тождественно равны нулю) передаточная функция звена может быть найдена как отношение изображений по Лапласу выходной и входной величин

,

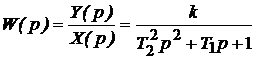где p=c+jω– комплексная величина.

При известной передаточной функции звена изображение по Лапласу его выходной величины можно найти из выражения

.

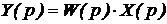Динамические свойства звена определяются по его временным и частотным характеристикам. Наиболее распространенными временными характеристиками являются переходная характеристика и функция веса.

Переходная функция, или переходная характеристика h(t), представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход единичного скачкообразного воздействия (рис. 1,а). Такое входное воздействие называется единичной ступенчатой функцией (рис. 1,б):

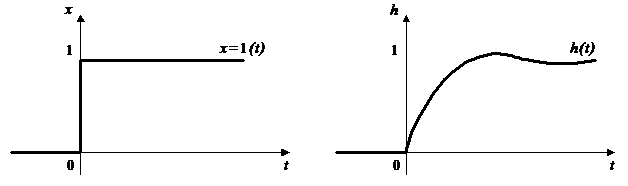а) б)

Рис.1. Переходная функция:

а - единичное скачкообразное воздействие 1(t); б – переходная характеристика h(t)

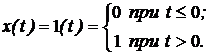
Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию (рис. 2,а). Единичная импульсная функция, или дельта-функция (рис. 2,б), представляет собой производную от единичной ступенчатой функции

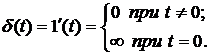
Основное свойство дельта функции заключается в том, что 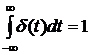, т.е. она имеет единичную площадь.

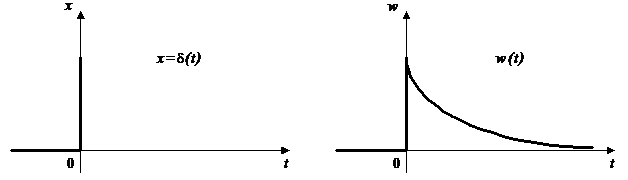а) б)

Рис.2. Функция веса:

а - единичный импульс d(t); б – функция веса w(t)

При описании линейных систем или звеньев важное значение имеют частотные характеристики. Они описывают установившиеся вынужденные колебания в системе при подаче на ее вход гармонического воздействия. В общем случае уравнение линейной системы можно записать так:

.

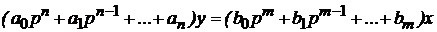Ее передаточная функция имеет вид

.

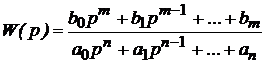Функцию W(jw), которую получают из передаточной функции W(p) при подстановке в нее p=jw, называют частотной передаточной функцией

.

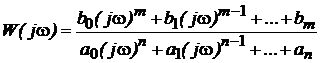Частотная передаточная функция является комплексной функцией от действительной переменной w, которая называется частотой.

Функцию W(jw) можно представить в виде

,

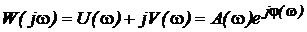где

.

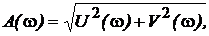
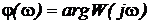Если 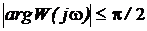, то .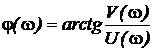

На комплексной плоскости частотная передаточная функция W(jw) определяет вектор, длина которого равна A(w), а аргумент, т.е. угол, образованный этим вектором с действительной положительной полуосью - j(w). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ¥ (иногда от -¥ до ¥), называют амплитудно-фазовой частотной характеристикой (АФЧХ).

Модуль 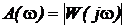называют амплитудной частотной функцией, а ее график – амплитудной частотной характеристикой.

Аргумент 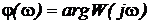называют фазовой частотной функцией, а ее график фазовой частотной характеристикой.

Кроме перечисленных частотных характеристик, используют еще логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ). При построении графиков этих характеристик по оси абсцисс откладывают логарифм частоты lgw. Единицей логарифма частоты является декада. Декадой называется интервал, на котором частота изменяется в 10 раз. Для графика ЛАЧХ по оси ординат откладывается функция 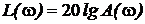, а для графика ЛФЧХ – функцию 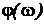. Ось ординат проводят через произвольную точку, а не через точку w=0, так как lgw ® - ¥ при w ® 0. Пример графиков ЛЧХ приведен на рис.3. Основные типовые звенья САУ приведены в табл. 1.

Рис.3. Логарифмические частотные характеристики

Порядок выполнения работы

1. Набрать модель звена.

2. Получить семейства графиков переходных характеристик звена при изменении:

- коэффициента передачи K=1…10;

- постоянных времени звена T=0,1…1;

- коэффициента демпфирования x=0,1…1.

3. По полученным графикам определить основные показатели переходных характеристик:

- величину установившегося значения h_уст;

- длительность переходного процесса t_пер;

- перерегулирование s ( ).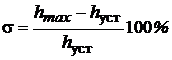

4. Получить семейства графиков частотных характеристик звена (АФЧХ, ЛАЧХ, ФЧХ) при параметрах, указанных в п.2.

5. Провести сравнительный анализ полученных характеристик, сделать выводы о влиянии параметров передаточных функций звеньев на их динамические характеристики.

Таблица 1

Основные типовые звенья САУ

Позиционные
1. Безинерционное
2. Апериодическое первого порядка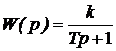
3. Апериодическое второго порядка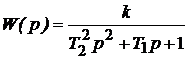
4. Колебательное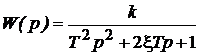
5. Консервативное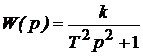
Интегрирующие
1. Идеальное интегрирующее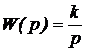
2. Интегрирующее с замедлением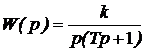
3. Изодромное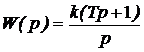
Дифференцирующие
1. Идеальное дифференцирующее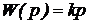
2. Дифференцирующее с замедлением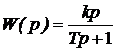

3. Контрольные вопросы

1. Какие временные характеристики САУ вы знаете и какова их связь с передаточными функциями САУ?

2. Какие виды частотных характеристик САУ вам известны и какой их физический смысл?

3. Какие типовые динамические звенья вы знаете, их передаточные функции и дифференциальные уравнения?

4. Как влияют параметры передаточных функций звеньев на их временные и частотные характеристики?

5. Каким образом выполняется расчет переходного процесса на выходе звена при произвольном входном воздействии по переходной и импульсной характеристикам?

6. Как получить частотные характеристики звеньев по их передаточным функциям?

7. Как строятся логарифмические частотные характеристики?

Ход работы:

1. Набираем модель идеального дифференцирующего звена в программе Matlab

2. По показаниям осциллографа получаем следующие частотные характеристики

Лабораторная работа №2. Исследование устойчивости линейных САУ

Цель работы

Исследовать замкнутую систему автоматического управления (ЗСАУ) при помощи критериев устойчивости Гурвица, Михайлова и Найквиста. Применить в работе ПО MATLAB.

Программа работы

1. Реализовать систему согласно следующим данным:

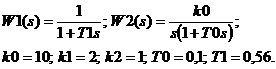
Структурная схема системы представлена на рисунке 1.

2. Проверить систему на устойчивость по алгебраическому критерию Гурвица. Сделать выводы.

3. Определить устойчивость системы по корням. Сделать выводы.

4. Изучить в MATLAB Help функции ltiview и margin и с их помощью получить информацию о переходной характеристике и оценить запас устойчивости.

5. Проверить систему на устойчивость по частотному критерию Михайлова. Сделать выводы.

6. Проверить систему на устойчивость по частотному критерию Найквиста. Сделать выводы.

Ход работы

Реализация системы

Передаточные функции звеньев САУ, представленной на рисунке (1), а также разомкнутой и замкнутой систем запишем в общем виде:

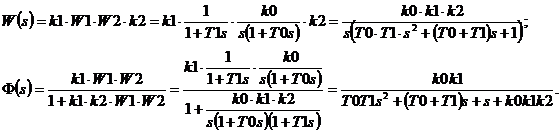
На рисунке 2 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения параметров САУ, а на рисунке 3 – представление ее в виде модели в пространстве состояний.